|
Can't Stop is a board game that was designed by Sid Sackson and released in 1980. It is a "press your luck" dice game in which players roll for dice and arranges them into two pairs. The sums of these pairs allow the player to progress their markers up the columns labeled with the values from 2 to 12. The goal of the game is to be the first to reach to top of three of these 11 columns. The height of the column is related to the probability that the sum will be rolled. The more likely the roll, the longer the column is. I was excited to find a copy of this game at a second hand shop recently. I've played Can't Stop online numerous times (at Board Game Arena) but this is a game where playing in-person seems better than virtual. The physical process of rolling and arranging the dice as well as interacting with other players makes for a better experience. I think it plays best with 2 or 3 players. They game is made for 2-4 players but I've seen people use the square plastic pieces from the game Advance to Boardwalk to add additional players in different colors. The Great Races
A nice user-created version of this paper and pencil game can be found at Board Game Geek. I like this version of the game because it is a quick game, with the "push-your-luck" aspect removed. Each player rolls just once, records their roll and then passes the dice to the next player. For a shorter game, you could play until 8 of the races are finished instead of completing all 11. Game at a GlanceBecause all the information about the game is contained on the game board, this is an excellent game for "Game at a Glance." Chad Williams has a collection of Game at a Glance images on his website, Beyond the Algorithm. Students are shown an image of a game in progress and could be asked a variety of questions.
I recently went camping and took this game along with me. I taught the game to several people (including kids) and because of the simple rules, they were all able to learn it in just minutes. Because all the pieces are plastic, they didn't blow away in the wind and if it got dirty, it could be easily rinsed off and cleaned. I think that this game would make a great addition to a mathematics classroom collection. What are your favourite games for the math classroom? Let me know! Nova Scotia Mathematics Curriculum Outcomes Mathematics 12 LR01 - Analyze puzzles and games that involve numerical and logical reasoning, using problem-solving strategies. Mathematics at Work 12 P01 - Students will be expected to analyze and interpret problems that involve probability. Mathematics at Work 11 N01 - Students will be expected to analyze puzzles and games that involve numerical reasoning, using problem-solving strategies. Mathematics Essentials 10 G4 - Compare predicted and experimental results for familiar situations involving chance, using technology to extend the number of experimental trials. Mathematics 8 SP02 - Students will be expected to solve problems involving the probability of independent events. Mathematics 7 SP06 - Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. EL
Summer is here and I've recently returned from a family vacation that included several lengthy flights. My son just turned eight years old and enjoys flying but can get a bit restless after a few hours on an airplane. Below are a few of the games and activities that we packed to make the time pass enjoyably. These games are best when they are small, lightweight, easy to pack and can be played on the limited space of an airplane tray table (often around 16.5" x 10.5" but there is no standard size). Games are ideally two player but if you're on a larger plane, you might be able to play a three player game. Pencil and Paper GamesGames that can be played with just pencil and paper are ideal for an airplane. We bring a few pencils and a tablet of paper with us for games, sketching or making notes. Here are a few of our favourite pencil and paper games:
Games with Dice, Cards and Counters
Commercial Board Games
Other StuffWhen on a long play ride I also bring snacks, a small LEGO set, and some art supplies to draw or colour with. Do you have suggestions for travel games to play with with your children? I'd love to hear your suggestions. EL
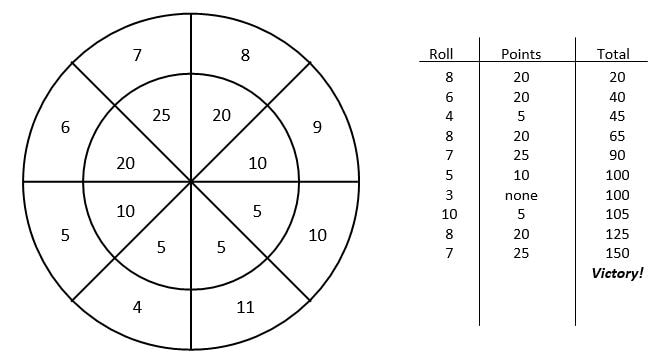
Below is a simple probability game that I've played with students for many years in a number of different courses. I don't really remember where I got it from but if you've seen it before, I'd love to know where it originated. I've found that students enjoy it and they really develop some good ideas about probability. Its similar to the Two-Dice Sum Game from Marilyn Burns but with some additional mental math for older students. InstructionsThis is a game for two or more players. Each player creates their own score card by drawing two concentric circles and then divide it into eight sectors. Choose eight different numbers between 2 and 12 and place them in the sectors in the outer ring. In the inner ring of the circle place numbers that add up to 100 (it is easiest to stick with multiples of 5). Roll two dice and add the numbers together, if the total is one of the numbers in the outer ring of your score card, you score that numbers value (the number in the inner ring). Players alternate rolling and scoring on their card until one of the players has 150 or more points (or to 100 for a bit shorter game). A google doc handout for this is available here. Sample Score CardTypically, the first time students play, they will randomly select numbers and values for each sector. After students have had the chance to play a few games, stop and ask them to look at different score cards to see if there any common characteristics of winning cards. What makes a good score card? Is it all just luck or are some cards better than others? Developing a StrategyWhat makes a good score card? Here are some common student observations:
Experimental ProbabilityYou might ask students to roll two dice a bunch of times and record which numbers come up each time. Create a bit dot plot or a bar graph at the front of the classroom using all of this data. Ask students to predict what the shape of this graph will be. You could also use an online tool to model lots of dice rolls to see how it compares to the class data. You could then discuss the theoretical probability for each sum and compare it to the data you gathered. I always find this a fun activity and a nice way to start a discussion about probability and strategy. A nice question to start the class on the following day would be a Would You Rather? math prompt, "Would you rather flip 2 coins and win if they match OR roll 2 dice and win if they don't match?" Another great follow up activity would be Don Steward's Dice Bingo. Nova Scotia Mathematics Curriculum Outcomes Mathematics at Work 12 P01 - Students will be expected to analyze and interpret problems that involve probability. Mathematics Essentials 10 G4 - Compare predicted and experimental results for familiar situations involving chance, using technology to extend the number of experimental trials. Mathematics 8 SP02 - Students will be expected to solve problems involving the probability of independent events. Mathematics 7 SP06 - Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. EL
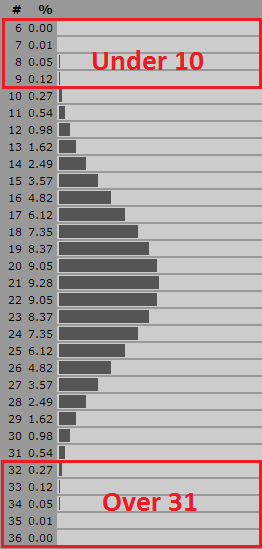
My son and I recently spent a lovely fall afternoon exploring the carnival games and amusement rides at a local fair. My son is quite adventurous when it comes to amusement park rides and is eager to try just about any ride that he meets the height requirement for. While we were walking through the midway, I spotted a carnival game called "Roll Down" that appeared to have a bit of mathematics involved. The object of this "game of skill" is to roll six balls down and inclined ramp to land in one of six numbered bins. If the sum of the six rolls is under 10 or over 31, you win. Is this game worth the $5 price to play? What are my chances of winning? Should I go for under 10 or over 31? Is this just a carnival scam or is there some skill involved? The bins are just wide enough for a ball to fit so it is very difficult to aim a ball with accuracy. You also have to question if the balls roll straight and if the board is smooth and level. Lets just assume that the balls fall into a random bin (you could then play an equivalent game at home by rolling 6, six-sided dice). With six balls, the smallest sum possible is 6 (all 1's) and the largest is 36 (all 6's). How many ways are there to get each possible value? There are only 31 possible sums (6-36) that you can score. To roll a sum of under 10, you can score 6, 7, 8 or 9. To roll a sum of over 31, you can score 32, 33, 34, 35, or 36. At first glance, it looks like you have a 9/31 chance of winning but this is not correct.
This reminds me of a bet in the casino game craps that looks good, but on further inspection is really bad. The field bet is a bet on the sum of the next roll of two six-sided dice. If the sum of the two dice is 2, 3, 4, 9, 10, 11 or 12 you win. If the sum is 5, 6, 7 or 8 then you lose. It has the illusion that there are more ways to win than lose, but you are much more likely to roll one of the losing numbers. With practice at Roll Down, you might be able to achieve better than the random results that I detailed above. Instead of this practice, I decided to spend my $5 at the concession stand to buy a hand-battered, deep fried corn dog. A midway concession stand can also be considered a bit of a gamble, but in this case it was a delicious win! EL
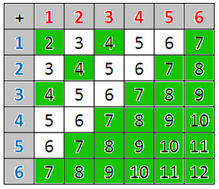
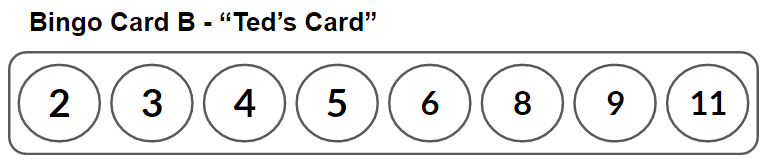
My son and I were looking through an issue of Fun to Learn Friends magazine recently and we ran across a game called "Spring Bingo". He was quite interested and wanted to give it a try. He is in grade primary and can subitize the pips on a six sided die as well as confidently sum the values on two dice. Just the skills we need to play this game. We played several times. At the end of most of the games, my son got frustrated trying to roll either a 2 or a 12. He doesn't quite understand why it takes so long to roll one of these numbers. George's bingo card has both of these numbers out of the eight numbers on the card. This seems unnecessarily cruel. Ted's card has the 2 but not the 12. This made me wonder if this is a fair game or if one of the cards has a better probability of winning. Time for some math... It appears that Card B is slightly better than Card A. I'm not sure if this would make a significant difference in the outcome of the game (i.e. rolling all the numbers on your card before your opponent does). I wonder what the average number of rolls it takes to complete each bingo card is? How much of an advantage does going first in this game give? If the player with Bingo Card A goes first does this equalize the advantage of the better Bingo Card B? These would be great questions for the Mathematics 12 research project outcome (MRPO1). To try to answer some of these questions, I thought that writing some code would be helpful. I know a grade 8 student that completed the Introduction and Intermediate Programming with Python courses from Art of Problem Solving. I contacted him and he graciously created a very nice Python program to simulate this game for me. I modified the code a bit so that it just plays one bingo card and counts how many rolls it takes to complete the card. The average number of rolls in 100,000 games for "George's Card" was 58. The average number of rolls in 100,000 games for "Ted's Card" was 48. I was a bit surprised that there was this much difference. Playing with Ted's bingo card appears to be an advantage. Next I modified the code again so that it plays the game with George going first to count how often George wins. In 100,000 games, when George went first, he won 50703 of the games. I again modified the code so that Ted plays first. In 100,000 games, when Ted went first, he won 50806 of the games. It seems that going first is an even greater advantage than having the better bingo card. What I really like about this game is that there are mathematical outcomes that can be addressed with this activity across a wide range of grade levels. At younger ages, students are practicing subitizing and adding numbers. One variation of this game is to play it solo. This might be a nice option for a math station. I found several examples of "Roll and Cover" games where students have a sheet of paper filled with numbers (from 1 to 6 or from 2 to 12) and students roll the die or dice and cover the number (with a token or a bingo dauber) when they roll it. Just do a Google search for "roll and cover math game" and you'll find lots of examples posted online.
For students looking for an opportunity for enrichment, they can make variations of this game. They could also write computer code to simulate this game (using Scratch or Python or some other language). They could also do some statistical analysis of the game to see how fair it is. There are so many options with this simple game. Nova Scotia Mathematics Curriculum Outcomes Mathematics 1 N02 - Students will be expected to recognize, at a glance, and name the quantity represented by familiar arrangements of 1 to 10 objects or dots. Mathematics 1 N09 - Students will be expected to demonstrate an understanding of the addition of two single-digit numbers and the corresponding subtraction, concretely, pictorially, and symbolically in join, separate, equalize/compare, and part-part-whole situations. Mathematics 2 N10 - Students will be expected to apply mental mathematics strategies to quickly recall basic addition facts to 18 and determine related subtraction facts. Mathematics 5 SP04 - Students will be expected to compare the likelihood of two possible outcomes occurring, using words such as less likely, equally likely, or more likely. Mathematics 6 SP04 - Students will be expected to demonstrate an understanding of probability by: identifying all possible outcomes of a probability experiment; differentiating between experimental and theoretical probability; determining the theoretical probability of outcomes in a probability experiment; determining the experimental probability of outcomes in a probability experiment; comparing experimental results with the theoretical probability for an experiment. Mathematics 7 SP06 - Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. Mathematics 8 SP02 - Students will be expected to solve problems involving the probability of independent events. Mathematics 10 Essentials G1 - Express probabilities of simple events as the number of favourable outcomes divided by the total number of outcomes Mathematics 12 P03 - Solve problems that involve the probability of two events. Mathematics 12 MRP01 - Research and give a presentation on topic that involves the application of mathematics. EL
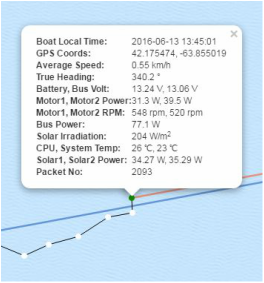
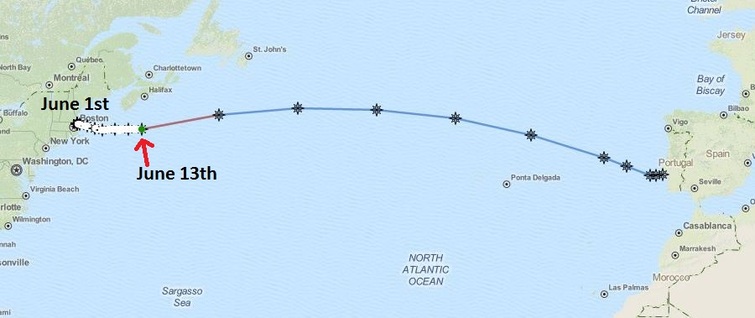
I recently read an article on Wired about the Solar Voyager. A pair of engineers, Isaac Penny and Christopher Sam Soon, designed and built an autonomous, solar powered vessel. On June 1st, 2016 the 18 foot vessel, named Solar Voyager set off on its trans-Atlantic adventure from Gloucester, Massachusetts to Portugal, a journey of more than 4800 kilometres. They are predicting that this trip will take 4 months, assuming that there are no catastrophic events mid-Atlantic. One cool thing about this trip is that the Solar Voyager reports it position and other data online every 15 minutes at http://www.solar-voyager.com/trackatlantic.html. Currently, about two-weeks into its journey, Solar Voyager is just South of Halifax, Nova Scotia where I live. The image below shows how far the Solar Voyager has traveled during its first two weeks. That is 1/8 of the time estimated for the crossing. Based on the information below, do you think that it will reach its destination in 4 months? What factors did you consider when making your estimation? Some factors you might consider are currents, weather, equipment malfunction, obstacles/collisions, wear and tear, etc. There are so many variables at play that it must be very hard to make an accurate estimation. Some Questions/Estimates for Students:
One of the coolest things about this project is that these young engineers "built Solar Voyager in their free time, undertaking this voyage simply for the challenge." How can I commandeer this type of intrinsic motivation for students in math class? What about this project made them want to work so hard "just for the challenge" and not for some extrinsic reward. Was it because they were the ones who selected and designed the task? Did they have just the right skills so that they felt confident that they would be successful? What is something that was relevant to their lives? How did this project captivate their curiosity? Data Points:
Update: Solar Voyager ran into some trouble south of Nova Scotia. It appears it got tangled in some fishing gear and the props and rudders were fouled. After drifting for over a week, the vessel was picked up by HMCS St. John's, a Canadian Navy offshore patrol vessel. EL
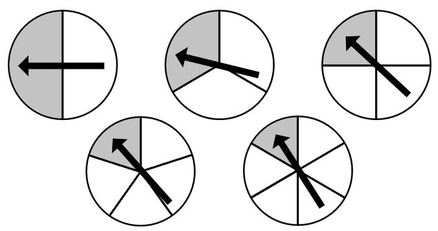
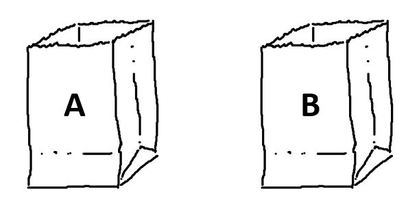
Open middle questions make for great classroom discussions. These are problems that have a closed beginning and end (i.e. an uncomplicated initial question and a single final answer) but an open middle where students can explore different paths and strategies to get to the solutions. Openmiddle.com is a great resource to find these types of questions. Below are a pair of open middle style problems I created for some of the probability outcomes in the NS Mathematics curriculum. Problem #1 - The Spinners Problem Directions: Select three of the spinners below (you may pick more than one of each) such that the total number of sectors in all three spinners totals 10. Select spinners so that the probability of all three spinners landing in the shaded sector is the smallest (or largest). Hint: There are only 4 different ways to select 3 spinners whose sectors add up to 10. In other words, how many ways can you a make a expression with 3 terms that add up to 10 using the numbers 2, 3, 4, 5 or 6. Solution: The four different options for selecting spinners are below. Option 1 yields the greatest probability and option 4 yields the least probability. 1) The greatest probability: 1/2 * 1/2 * 1/6 = 1/24 2) 1/2 * 1/3 * 1/5 = 1/30 3) 1/4 * 1/4 * 1/2 = 1/32 4) The least probability: 1/3 * 1/3 * 1/4 = 1/36 Extension: How would this problem change if you removed the restriction of exactly three spinners? If you could create as many spinners as you wanted such that the sectors totaled to 10 (e.g. 1 spinner with 10 sectors or 5 spinners with 2 sectors, etc.) what would the greatest probability be? 1) The greatest probability: 1/10 = 1/10 2) 1/2 * 1/2 * 1/2 * 1/2 * 1/2 = 1/32 3) 1/5 * 1/5 = 1/25 Problem #2 - The Marbles Problem Directions: "There are _____ red marbles and _____ blue marbles in Bag A. There are _____ red marbles and _____ green marbles in Bag B. " Place a different whole number from 1 to 9 in each blank to make the probability of drawing a red marble from either bag A or B the same. How many different ways can you find to do this? Hint: How can you have a different number of red marbles in each bag but the same probability of selecting a red marble? Solutions: The are 40 different solutions! I first found 5 solutions and then realized that if you just flip the number of red marbles with the other colour, you get another 5 solutions. Then I realized that if you swap the bags, you double the solutions again. I made a Python program to check my work and realized that I had still missed a few and added them in. 1) Bag A: 1 red and 2 blue; Bag B: 3 red and 6 green For each solution below, the following 3 rearrangements are possible. 1B) Bag A: 2 red and 1 blue; Bag B: 6 red and 3 green 1C) Bag A: 3 red and 6 blue; Bag B: 1 red and 2 green 1D) Bag A: 6 red and 3 blue; Bag B: 2 red and 1 green 2) Bag A: 1 red and 2 blue; Bag B: 4 red and 8 green 3) Bag A: 1 red and 3 blue; Bag B: 2 red and 6 green 4) Bag A: 1 red and 4 blue; Bag B: 2 red and 8 green 5) Bag A: 2 red and 3 blue; Bag B: 4 red and 6 green 6) Bag A: 2 red and 3 blue; Bag B: 6 red and 9 green 7) Bag A: 2 red and 4 blue; Bag B: 3 red and 6 green 8) Bag A: 2 red and 6 blue; Bag B: 3 red and 9 green 9) Bag A: 3 red and 4 blue; Bag B: 6 red and 8 green 10) Bag A: 3 red and 6 blue; Bag B: 4 red and 8 green If you want to make this problem a bit easier, just use the numbers from 1 to 6. This gives a total of 16 solutions. These would be 1, 3, 5, and 7 from above plus the 3 additional re-arrangements of each. Extension: Make the number of green marbles a 2 digit number. Nova Scotia Mathematics Curriculum Outcomes Mathematics 7 - SP06 Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. Mathematics 8 - SP02 Students will be expected to solve problems involving the probability of independent events. Mathematics 10 Essentials - G1 Express probabilities of simple events as the number of favourable outcomes divided by the total number of outcomes Mathematics 12 - P03 Solve problems that involve the probability of two events. EL
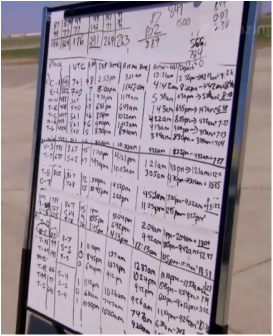
As a math teacher, I always love to see folks doing real math on television. Last week, on The Amazing Race Canada (Season 3, Episode 7), there was a 'tricky' mathematical challenge. Contestants were given a list of Air Canada flights and asked to create a flight plan using Air Canada destinations from around the world. They had to find a set of flights that had a total flight time of 25 hours (or 1500 minutes). They also had to ensure they used "a combination of routes that travel to at least three continents". Calculating the flight time was the first hurdle. Since arrival and departures are listed in local time and the vast majority of these flights crossed multiple time zones, contestants had to use the universal time code for each city to correct for time changes. A number of teams were confused right from the start (there was a lot of fixed mindset talk from the contestants). One team used an 'Express Pass' to skip this challenge while two other teams gave up and took a 2 hour time penalty instead of continuing with the challenge, That is a lot of flights! There are 12 flights listed on the Europe board, 11 flights on the Asia Pacific board and 15 flights on The Americas board. If we use just one flight from each board (so that we visit three continents), there are a total of 1980 combinations (12*11*15=1980). The rules state that we have to visit at least three continents but it doesn't say how many flight to use so we could have a flight plan with more than three flights. If we add one additional flight to make a flight plan with four flights, now we have 69300 possible flight plans (12*11*15*35=69300... one flight from each board and any one of the remaining 35 flights). That is a LOT of trial and error. The two solutions shown on the episode contained 4 flights. Are there any 3 flight plans that would work? Here is what I did.
First I got some screen captures of the flight boards so I could read all the flight times. Then I put them all into an Excel spreadsheet to calculate the flight times in minutes. Next I played with Excel for about an hour to try to find an efficient way to calculate all the combinations of flights that I wanted to try and then gave up. Instead, I created a quick program in Python to calculate all the possible sets with just three flight plans. This turned out to be much easier than using Excel (just 8 lines of code). AList=[924,731,635,1016,802,640,831,744,767,658,772] BList=[566,453,488,408,447,433,424,461,457,490,522,514] CList=[343,87,99,192,325,616,324,363,650,335,337,77,183,640,316] for i in AList: for j in BList: for k in CList: if i+j+k==1500: print 'Eureka!',i,j,k Now, assuming that I calculated the correct flight times in my Excel spreadsheet, this gave me three possible solutions: 1- AC025 Vancouver to Shanghai, AC824 Toronto to Amsterdam, AC541 Toronto to Seattle 731 + 453 + 361 = 1500 minutes 2- AC084 Toronto to Tel Aviv, AC898 Edmonton to London, AC962 Toronto to Bogota 635 + 522 + 343 = 1500 minutes 3- AC056 Toronto to Dubai, AC1904 Toronto to Edinburgh, AC1973 Halifax to Calgary 767 + 408 +325 = 1500 minutes The two solutions that were shown on the episode using four flights are below: AC480 Toronto to Montreal, AC918 Toronto to Miamai, AC882 Toronto to Copenhagen, AC007 Vancouver to Hong Kong 77 + 192 + 447 + 784 = 1500 minutes AC230 Vancouver to Calgary, AC541 Vancouver to Seattle, AC1910 Montreal to Nice, AC009 Calgary to Tokyo 87 + 316 + 457 + 640 = 1500 minutes
There was a nice article posted online that interviewed the Air Canada captain that handed out the clue cards for the challenge. He mentions the factors that he said made this such a challenging competition.
EL |
Categories
All
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||




















 RSS Feed
RSS Feed