|
I was recently looking for an activity to explore a linear relationship, preferable one that included some practice with decimals. I found a few examples but none of them really seemed to satisfy what I was looking for. Here are a few of my criteria for good experiments to explore function relationships:
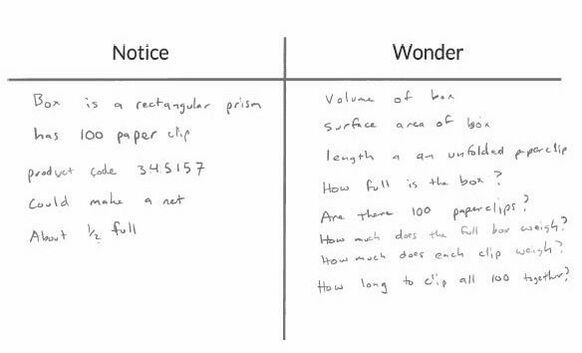
Notice and WonderThere were some great questions about volume and surface area, weight, and size of the paper clips (what is a #4 sized paper clip?). The questions the we went on to investigate was how long would it take to make a paper clip chain from all 100 paper clips. I was inspired by Dan Meyer's Guinness World Record for the longest paperclip chain in 24 hours. Dan blogged about breaking the record as well as asking student to see how many paperclips they could chain in one minute. EstimationI asked students to estimate how long they thought it would take to create a chain of 100 paper clips. I also asked them to think about an estimate that they know was too low (that creating a chain this fast was not possible) and too high (that they would have no problem creating a chain in this time even going slowly). Most students thought that a time between 5 and 6 minutes was a good "just right" estimate. Gathering Data
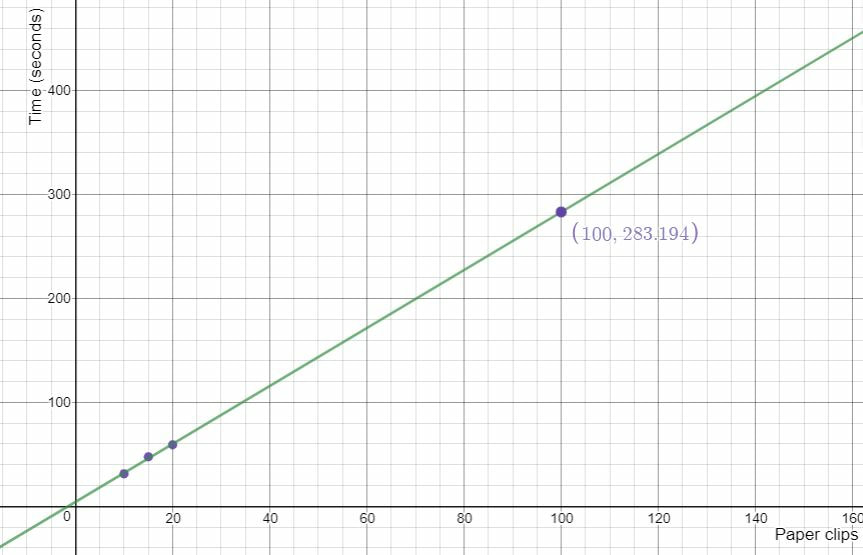
Revising EstimatesAfter collecting and analyzing some data, I ask students if they'd like to revise their estimate for 100 paper clips. Then we test their revised estimate using a plot of the values they collected and extrapolating. Below is one student's data plotted in Desmos. They estimated 300 seconds (5 minutes) to chain all 100 paperclips. This lesson could be modified to include outcomes from a number of different grade levels. I closed the lesson by showing students the record for the most paper clips linked together in one minute and asked students how they would compare. Nova Scotia Mathematics Curriculum Outcomes Mathematics 6 SP01 - Students will be expected to create, label, and interpret line graphs to draw conclusions. Mathematics 6 SP02 - Students will be expected to select, justify, and use appropriate methods of collecting data, including questionnaires, experiments, databases, and electronic media. Mathematics 6 SP03 - Students will be expected to graph collected data and analyze the graph to solve problems. Mathematics 7 PR02 - Students will be expected to create a table of values from a linear relation, graph the table of values, and analyze the graph to draw conclusions and solve problems. Mathematics 7 N02 - Students will be expected to demonstrate an understanding of the addition, subtraction, multiplication and division of decimals to solve problems (for more than one-digit divisors or more than two-digit multipliers, the use of technology is expected). Mathematics 7 SP01 - Students will be expected to demonstrate an understanding of central tendency and range by: determining the measures of central tendency (mean, median, mode) and range; determining the most appropriate measures of central tendency to report findings. Mathematics 7 SP02 - Students will be expected to determine the effect on the mean, median, and mode when an outlier is included in a data set. EL
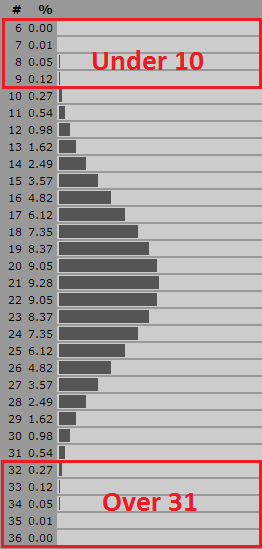
My son and I recently spent a lovely fall afternoon exploring the carnival games and amusement rides at a local fair. My son is quite adventurous when it comes to amusement park rides and is eager to try just about any ride that he meets the height requirement for. While we were walking through the midway, I spotted a carnival game called "Roll Down" that appeared to have a bit of mathematics involved. The object of this "game of skill" is to roll six balls down and inclined ramp to land in one of six numbered bins. If the sum of the six rolls is under 10 or over 31, you win. Is this game worth the $5 price to play? What are my chances of winning? Should I go for under 10 or over 31? Is this just a carnival scam or is there some skill involved? The bins are just wide enough for a ball to fit so it is very difficult to aim a ball with accuracy. You also have to question if the balls roll straight and if the board is smooth and level. Lets just assume that the balls fall into a random bin (you could then play an equivalent game at home by rolling 6, six-sided dice). With six balls, the smallest sum possible is 6 (all 1's) and the largest is 36 (all 6's). How many ways are there to get each possible value? There are only 31 possible sums (6-36) that you can score. To roll a sum of under 10, you can score 6, 7, 8 or 9. To roll a sum of over 31, you can score 32, 33, 34, 35, or 36. At first glance, it looks like you have a 9/31 chance of winning but this is not correct.
This reminds me of a bet in the casino game craps that looks good, but on further inspection is really bad. The field bet is a bet on the sum of the next roll of two six-sided dice. If the sum of the two dice is 2, 3, 4, 9, 10, 11 or 12 you win. If the sum is 5, 6, 7 or 8 then you lose. It has the illusion that there are more ways to win than lose, but you are much more likely to roll one of the losing numbers. With practice at Roll Down, you might be able to achieve better than the random results that I detailed above. Instead of this practice, I decided to spend my $5 at the concession stand to buy a hand-battered, deep fried corn dog. A midway concession stand can also be considered a bit of a gamble, but in this case it was a delicious win! EL
Sherman K. Stein, in the preface of his textbook Mathematics, The Man Made Universe, says "Mathematics is completely the work of man. Each theorem, each proof, is the product of the human mind. In mathematics all the cards can be put on the table. In this sense, mathematics is concrete, whereas the world is abstract." The order of operations is a mathematical convention that has been developed and refined over centuries by many mathematicians. Just about every student, at some point in their mathematical education, will run across the mnemonic BEDMAS (or PEDMAS if you live in the US). The usefulness of this mnemonic can be debated (Tina Cardone, the author of Nix the Tricks, wrote an article regarding this for the NCTM). I recently chatted with a teacher who was looking for resources to help his grade 7 students practice using the order of operations with decimal numbers. I created a "row game" for his students to practice this skill. A "row game" is an activity for students to work with a partner to evaluate a series of expressions. The expressions are written in two columns. One student evaluates the expressions in the left column and the other student evaluates the expressions in the right column. The expressions in each row evaluate to the same value. If the students don't get the same answer, they can work together to determine where the error was made. There are two reasons that I like row games. The first is that students get instant feedback. They don't need to wait for a teacher to correct and return a sheet to know if they are being successful. The second reason is that it gets students to work together to find their mistakes. The teacher can then focus on providing assistance to students who are having real conceptual difficulties, not just making small computational errors. Kate Nowak has created a shared Google drive folder where a large collection of row games are stored. A link to my row game for order of operations with decimals is below.
Confusion regarding the order of operations has lead to many debates and arguments on Facebook about the correct way to evaluate expressions. You might see expressions such as "6 ÷ 2(1 + 2)" or "48 ÷ 2(9 + 3)" discussed. These might be used to start a lively debate in math class. I really like Vi Hart's take on these types of problems. Take a moment to watch the video below. Vi's contention is that expressions like these are ambiguous and it is incumbent upon the author of the expression to add brackets or other grouping symbols to make their mathematical expression clear. The placement of implicit multiplication (sometimes called multiplication by juxtaposition or simply putting symbols side by side) in the order of operations has not been settled by mathematicians such that is is part of the convention for the order of operations. Despite this, calculators and computers have to make a decision on how to interpret this. You will find calculators that give different answers for these types of expressions. The Math Forum writes, "I suppose I agree with you that it would be easier and perhaps more consistent to give multiplication precedence over division everywhere; but of course there is no authority to decree this, so the more prudent approach is probably just to recognize that there really isn't any universal rule. " One method of avoiding this confusion is to write expressions is using Reverse Polish (RPN) notation. I'm old enough to have owned an HP calculator that used this notation. In RPN, the operator always follows all of its operands. For example, instead of writing "(1+2)÷(3+4)", you would write "1 2 + 3 4 + ÷". RPN often requires fewer key strokes to enter on a calculator because parentheses are not required. It is however more difficult to learn. Nova Scotia Mathematics Curriculum Outcomes Grade 9 N04 - Students will be expected to explain and apply the order of operations, including exponents, with and without technology. Grade 7 N02 - Students will be expected to demonstrate an understanding of the addition, subtraction, multiplication and division of decimals to solve problems (for more than one-digit divisors or more than two-digit multipliers, the use of technology is expected). EL
I recently discovered that the way that prices are shown on rate signs for motor vehicle fuel varies quite a bit. Some display the current price in dollars, some in cents and some, confusingly, show both dollars and cents. None of the signs that I found actually showed the units being displayed ($, ¢, L, gal., etc). I decided that it would be a good topic for a Which One Doesn't Belong discussion that would focus in on decimals, place value and fractions as well as currency and volume measurement. Here are some suggestions why each image might not belong as well as some additional information for discussion: Top Left: This is the only fuel price sign with both a decimal and a fraction. It is from a Costco in Oregon. The price is $2.29 and 9/10¢ per gallon. Both dollars and cents are used in this price. If you assumed that the entire price was listed in dollars, then $2.29 and $9/10 would actually give a price of $2.29 + $0.9 = $3.19. Top Right: This is the only fuel price sign with just one decimal. It is from a Shell station in Halifax, NS and is in Canadian cents per litre. In Nova Scotia, the price often doesn't end with the standard 9/10¢ since the price is regulated by the Nova Scotia Utility and Review Board and only changes once per week. Bottom Left: This is the only fuel price sign with two decimals. It is from an Atlantic Superstore gas station in Dartmouth, NS. Similar to the sign above it (top left), it displays a price of $1.00 and 0.5¢ per litre. While probably not confusing to the average motorist, I find the use of two decimals to be mathematically troubling. Why not just list the price as $1.005? Bottom Right: This is the only fuel price sign with no decimals. It is from a 76 gas station in Oregon and is in US cents per gallon. It is interesting to note that Oregon and New Jersey are the only two US states with laws prohibiting self serve at gas stations. This sign mentions "Mini Serve" to note that an attendant operates the pumps but does not provide any of the other services you'd expect with full service.
Nova Scotia Mathematics Curriculum Outcomes Grade 5 N09 - Students will be expected to relate decimals to fractions and fractions to decimals (to thousandths). Grade 5 N10 - Students will be expected to compare and order decimals (to thousandths) by using benchmarks, place value, and equivalent decimals. Grade 6 N01 - Students will be expected to demonstrate an understanding of place value for numbers greater than one million and less than one-thousandth. Grade 7 N07 - Students will be expected to compare, order, and position positive fractions, positive decimals (to thousandths), and whole numbers by using benchmarks, place value, and equivalent fractions and/or decimals. EL
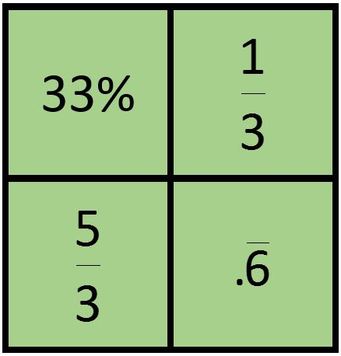
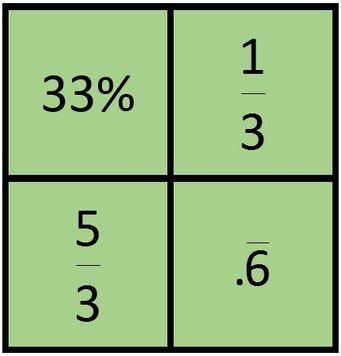
I've mentioned in the past that I think WODB questions are a great way to begin a lesson and engage students in a mathematical discussions. Below is one such question I created for grade 7 students. Most are working in or have recently finished Unit 3 on Fractions, Decimals and Percents. The question below might be a good review now that students have the language and vocabulary to debate which one doesn't belong. Here are some suggestions and why each number might not belong: Top Left: It is the only percentage and it is the only number with a tens place. It is also the only number without a vinculum. This is also the only number that is not an exact multiple of 1/3. 33% would be 33/100 and so is just a bit less than 1/3. If all the numbers were written as decimals, this would be the only terminating decimal. Top Right: It is the only number that would be a unit fraction when written as a fraction Bottom Left: It is the only value "greater than one". 33 is great than one but since it is a percentage, it represents 33/100. Bottom Right: This is the only even number and also the only term without the digit 3 in it. It is also the only number written as a decimal and the only box with just one digit in it. If your students are not used to participating in this type of discussion, you might scaffold it by first having students brainstorm and list the vocabulary and math terminology that might be used in the coming conversation. This might be especially helpful in a late French Immersion classroom where all students might not be familiar with the correct vocabulary. Having it listed on the board might help students feel more confidence in joining in the conversation. For the fractions, decimals and percent WODB above here is a list of vocabulary students might come up with: unit fraction, improper fraction, mixed number, percent, terminating decimal, non-terminating decimal, even and odd. A special thanks to Matt Murphy (@Lemurph42) for the following translation of the above post! Lequel n’appartient pas? Les Fractions, Décimaux et Pourcentages.J’ai déjà dit que je trouve les questions de WODB font un bon départ pour engager les élèves en discussions mathématiques. Ci-dessous il y a une telle question que j’ai créé pour les élèves de 7e année. La plupart de nos classes ont déjà complété chapitre 3 (fractions, décimaux et pourcentages), ou le finiront bientôt. L’exemple suivant pourrait être une bonne révision maintenant que les élèves ont le vocabulaire nécessaire pour s’engager en débat. Voici les arguments pour chaque choix : Gauche supérieure: c’est la seule pourcentage et c’est le seul nombre avec un chiffre à la position des dixaines. C’est aussi le seul nombre qui n’a pas une surlignéation. Ce n’est pas un multiple de 1/3 (33 % sera 33/100, un peu plus petit que 1/3). Si tous les nombre seront écrit comme décimal, c’est le seul qui termine. Droite supérieur: c’est le seul qui est une fraction unitaire. Gauche inférieur: le seul nombre qui est « plus grand qu’une ». C’est vrai que 33 est plus grand qu’une, mais puisque c’est une pourcentage, la valeur est 33/100 en réalité. Droite inférieure: c’est le seul nombre paire et il ne contient pas le chiffre 3. C’est le seule nombre en forme décimal et le seul qui ne contient qu’un chiffre. Si vos élèves ne sont pas habitués à tel sorte de discussions, vous pouvez utiliser l’échafaudage. D’abord, demandez aux élèves de faire un remue-ménginges du vocabulaire mathématique qui pourrait être utile dans la conversation. Ceci pourrait être utile dans une classe d’immersion tardive dont les élèves ne seront pas familiers avec tous les mots de vocabulaire. La confiance des élèves augmentera avec une liste mots disponible au tableau, faisant qu’ils seront plus capables à participer. Pour la WODB des fractions, décimaux et pourcentages en haut, voici quelques mots de vocabulaire que, peut-être, vos élèves fourniront: fraction impropre, nombre mixte, pourcentage, décimal terminé, décimal illimité, paire, impaire Nova Scotia Mathematics Curriculum Outcomes Grade 7 N07 - Students will be expected to compare, order, and position positive fractions, positive decimals (to thousandths), and whole numbers by using benchmarks, place value, and equivalent fractions and/or decimals. Grade 7 N03 - Students will be expected to solve problems involving percents from 1% to 100% (limited to whole numbers). EL
|
Categories
All
|
||||||||||||||||









 RSS Feed
RSS Feed