|
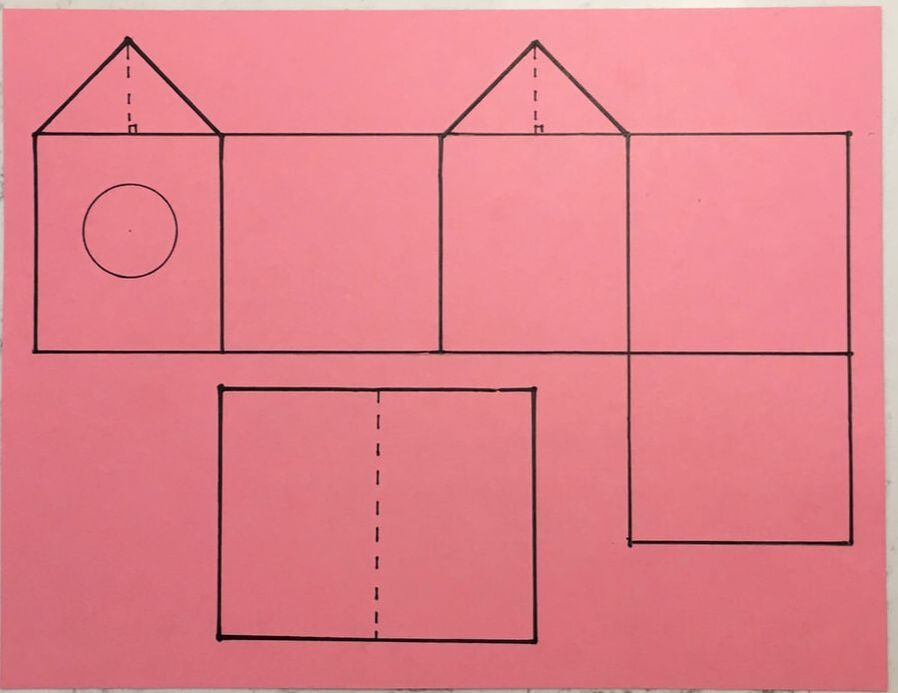
"Design and build a model birdhouse from a single sheet of 8.5" x 11" sheet of paper." This open ended activity seems simple at first but will require careful planning and attention to detail for students to be successful. You might start off this activity by showing a photo of an actual birdhouse and asking students to brainstorm the features of a good birdhouse. A website like this one might be a good guide. Next you can talk about the expectations for their model birdhouse design:
Students should then be asked to create a design. The design should minimize wasted paper (i.e. use as much of the page as possible) and be easy to assemble (i.e. minimize the number of pieces you have to cut out and assemble). You can then show students an example of a finished design. ProcedureStep 1 - Students should brainstorm some possible designs (at least two) on a piece of looseleaf Step 2 - Ask students to pick their favourite idea and share it with the teacher Step 3 - Once the teacher approves their design, students are given a piece of card stock. They can then lay out their design with a ruler Step 4 - When finished, students will measure and record all dimensions for their model. Students then calculate the surface area and volume of their design Step 5 - The final step is to cut out and assemble their birdhouse model! Here is a Google slides document that could be used to introduce the activity to students and make the expectations clear. Math at Work 10 Activity: One teacher modified this activity by giving students a selection of designs to choose from instead of designing their own (here are links to pdf template 1 and template 2). Students then did all of the measurements and computations and had to determine costs for shingles on the roof, siding for the walls and paint for the interior. Here is a handout similar to the one she used. Extensions: If you were to take your model and use it to build an actual birdhouse from wood, what would have to change? By what scale factor would you have to increase the size? How would building with 3/4" thick wood (instead of flat paper) change the size of the pieces needed? What supplies would you need and how much would it cost to build? NS Outcomes: Mathematics 9 - G01 Students will be expected to determine the surface area of composite 3-D objects to solve problems Mathematics 10 - M03 Students will be expected to solve problems, using SI and imperial units, that involve the surface area and volume of 3-D objects, including right cones, right cylinders, right prisms, right pyramids, and spheres. Mathematic at Work 10 - M04 Students will be expected to solve problems that involve SI and imperial area measurements of regular, composite, and irregular 2-D shapes and 3-D objects, including decimal and fractional measurements, and verify the solutions. Mathematics Essentials 12 - 2.4 Sketch and construct a model which will enable a student to show others some mathematics involved in a career interest EL
A couple of weeks ago, I saw a tweet from Don Fraser (@DonFraser9) in which he noticed that every box of Raisin Bran says "2 scoops" no matter what it's size is. I was recently talking with a teacher about the Percent, Ratio, and Rate unit for grade 8 math and I was reminded of Don's question. This deserved some additional investigation so I headed to the grocery store to gather the facts. At my local store, Kellogg's Raisin Bran is available in 3 sizes as seen below. Questions to Consider1. Rate: Which size box of cereal has the best unit price (g/$)? 2. Ratio: If there are two scoops in the regular size box, to preserve the same proportion of raisins, how many scoops should there be in the Family Size and Jumbo Size box? Alternatively, if the ideal proportion of raisins is to be found in a different size box, how many scoops should there be in the other two sizes? 3. Ratio: A "scoop" is a non-standard unit of measure. If the amount of raisins in each box stays the same proportion, then how should the size of the scoops change in order to maintain that proportion in each size box? 4. Volume: These boxes all have different volumes. Determine the volume of each and compare it to the weigh of cereal in that box. Does this rate stay the same? If it doesn't, what does it tell you about the amount of empty space in the box? How do the dimensions of each box compare? Are the different sized boxes similar shapes? Some additional Raisin Bran resources: Nova Scotia Mathematics Curriculum Outcomes Grade 8 M03 - Students will be expected to determine the surface area of right rectangular prisms, right triangular prisms, and right cylinders to solve problems. Grade 8 M04 - Students will be expected to develop and apply formulas for determining the volume of right rectangular prisms, right triangular prisms, and right cylinders. Grade 8 N04 - Students will be expected to demonstrate an understanding of ratio and rate. Grade 8 N05 - Students will be expected to solve problems that involve rates, ratios, and proportional reasoning. Grade 9 SP03 - Students will be expected to develop and implement a project plan for the collection, display, and analysis of data by: formulating a question for investigation; choosing a data collection method that includes social considerations; selecting a population or a sample; collecting the data; displaying the collected data in an appropriate manner; drawing conclusions to answer the question. Mathematics 12 MRP01 - Research and give a presentation on topic that involves the application of mathematics. EL
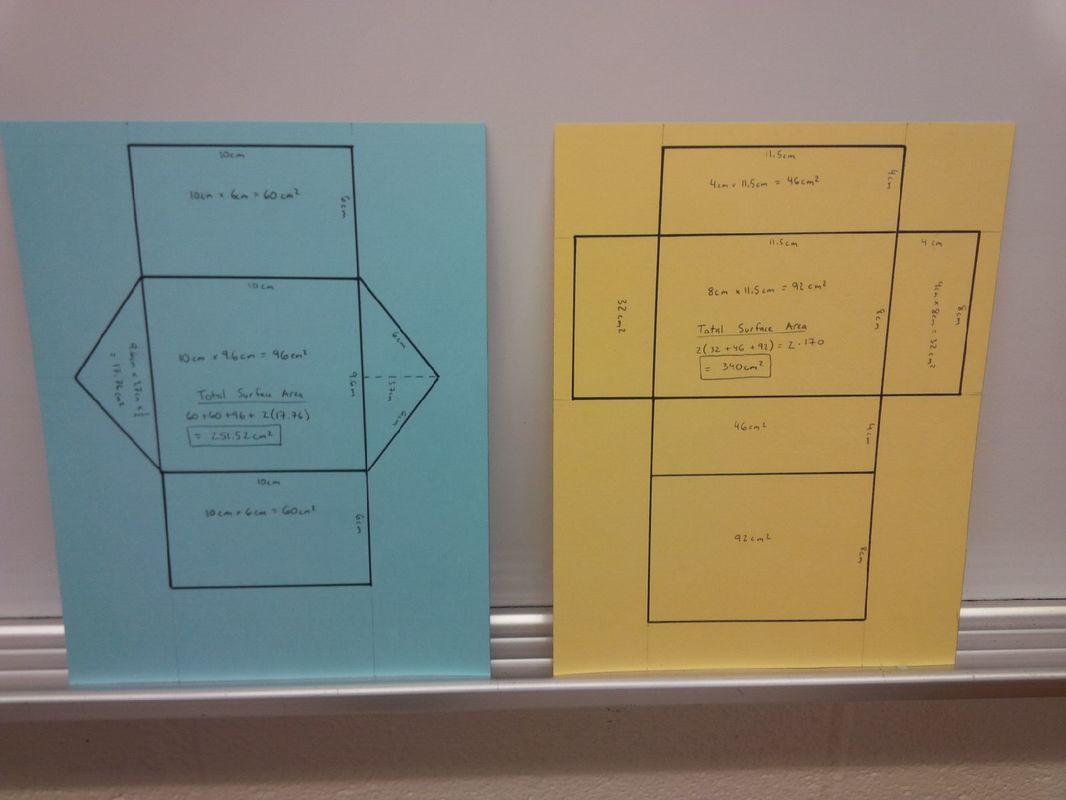
Constructing Rectangular and Triangular PrismsDetermining the surface area of a prism can get a bit stale. Textbooks contain lots of pictures of various right rectangular and triangular prisms. These prisms are carefully labeled with the exact information that a student needs. Students are given the task of inserting these numbers into a formula and doing some basic calculations. These types of problems often don't require much thought. I've recently had the pleasure of working in some junior high classrooms. We were looking for a more hands-on and thought provoking activity for surface area. We were also looking for an activity in which students could be creative. This is what we came up with. Students, working in pairs, are given either a yellow or blue piece of coverstock. Students with a yellow piece are asked to design and draw the net of a right rectangular prism. Students with a blue piece are asked to design and draw the net of a right triangular prism. Students can draw whatever size or shape prism they wish as long as it covers the majority of the paper (at least half). Students use a ruler to carefully draw and measure the net. They measure and label the length and width of each face and calculate the area of each face on the net they have drawn. Once students have accurately drawn their nets and labeled the area of each side, a teacher will review their work. If it is an accurate net, the teacher will give the students a pair of scissors to cut it out. Make sure students do their calculations inside the net so that it is not lost when they cut it out. Once cut out, students can fold and tape their prism. Students found this activity to be more challenging than they expected. Several had to start over after realizing that the prism they started wouldn't fit on the page or their net wouldn't fold into a proper prism. You could extend this activity by having students tape their nets inside out (with the calculations on the inside) and then challenging them to order the prisms from least surface area to greatest surface area. Why I Like This Task
Double the Surface Area
Nova Scotia Mathematics Curriculum Outcomes Grade 8 M02 - Students will be expected to draw and construct nets for 3-D objects. Grade 8 M03 - Students will be expected to determine the surface area of right rectangular prisms, right triangular prisms, and right cylinders to solve problems. Grade 9 G01 - Students will be expected to determine the surface area of composite 3-D objects to solve problems Math at Work 11 M01 - Students will be expected to solve problems that involve SI and imperial units in surface area measurements and verify the solutions. EL
There are some really big doors around Halifax. The door on Irving Shipbuilding's Halifax Shipyard Assembly and Ultra Hall facility is big enough for large "mega-blocks" of ships under construction to pass through. The doors at IMP Aerospace's Hangar #9 at the Stanfield International airport is big enough for large aircraft to pass through. Which door do you think is the largest? What Do You Mean by Largest?The first thing you might want to do is settle on what you mean by "largest". Do you mean width, height, area, mass or some other measurement? Each of these doors might be the largest for a specific measurement. For example, the aircraft hangar door is made of metal and quite probably has more mass than the shipyard door which is constructed of a polyester fabric. Estimating DimensionsThe shipyard door is really tall but the aircraft hangar door is really wide. Below are pictures of the two facilities from Google earth with the same scale so that you can compare the buildings that these doors are on. https://www.google.ca/maps/@44.6674497,-63.5972041,542m/data=!3m1!1e3 https://www.google.ca/maps/@44.8701869,-63.5322158,573m/data=!3m1!1e3 Door Dimensions and Surface Area
So the shipyard door has the largest height and the largest area but the hangar door has the largest width and the largest mass. Would you call this a tie? How would you determine the winner?
More Big DoorsDo you know of other big doors around Halifax? Have you seen bigger doors in other parts of Nova Scotia or the rest of Canada? What is your definition of door? Note of Thanks: I want to say thank you to the people at both Irving Shipyard and IMP Aerospace who were very helpful providing information for this post. EL
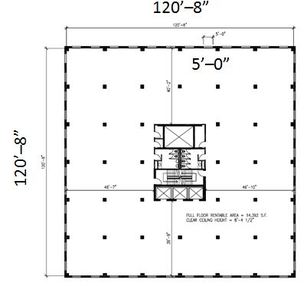
I drive past this building every day on my way to work. It is Young Tower at 6080 Young Street in Halifax. I think it is pretty interesting... I used this picture as a problem solving warm up activity for a group of grade 10 math teachers recently. I gave each group of teachers a large piece of chart paper and asked them to divide the paper in half with a line. I asked teachers to brainstorm what they notice about this picture and record it on one half of their chart paper. I asked them to look at the picture using a number of lenses. What would an architect notice about this image? What would a person who worked at this building notice about this picture? What would a mathematician notice about this picture? After about 5 minutes of brainstorming, I asked each group to tell me one thing they noticed and I recorded it at the front of the room. Groups noticed things like the number and size of windows on the building ("about half the lateral surface is glass"), the shape of the building ("almost a cube"), the picture must have been taken on a weekend because there are very few cars in the parking lot, and the weather was really nice that day. Next I asked them to brainstorm what they wonder about this picture and record in on the other half of their chart paper. If this picture was the start of a math problem, what could that math problem be? What things that they noticed sparked their curiosity? After another 5 minutes, I asked each group once again to tell me one thing that they wondered. After looking at all the questions that the groups posed, we selected one and asked everyone to estimate an answer to that question. I also asked them what information would they need to make a more accurate estimate. Once they had an initial estimate, I gave them some additional information about the building and let them revise their estimate. We had several really interesting questions posed by groups. Some questions concerned the shape of the building, like "How close to a perfect cube is this building?" Other questions focused on finance such as, "How much revenue is generated by leasing all of the office space in this building?" One of my favourite 'wonderings' was, "How much wrapping paper would it take to wrap this building up like a Christmas present?"
This "I Notice/I Wonder" problem solving strategy is one that I saw shared by Max Ray-Riek from the Math Forum. He has a blog where he talks about Noticing and Wondering in High School. This strategy starts off with brainstorming to let students get familiar and engaged with a problem situation before jumping into a specific question to solve. By having students come up with questions, you'll often get more engagement and interest. It also allows you to respond to interesting suggestions from students that you might not have considered. It allows everyone in the class meaningful participation in the conversation because everyone has something that they can notice. This strategy might also create additional opportunities for differentiation by using several different questions that students suggested. EL
One of my favourite activities recently has been Fawn Nguyen's Snap Hotel. This activity can also be found on the NCTM Illuminations website. You might see this activity online under a few different names... my favourite is Hotel^3. It is an engaging problem solving task. Students are given 50 multi-link cubes and instructed to build a model hotel. Each cube represents one hotel room. Some rooms are more desirable than others and can be rented for higher prices. The number of windows and whether or not the room has a roof determine the rental price. Students also have to consider costs associated with property and height. The hotels that students create in this activity remind me of Montreal's Habitat 67. Students might talk about the costs and benefits of this type of architecture. This activity can be used to assess a number of Nova Scotia mathematics curriculum outcomes. The Rules - As a team, build a hotel that yields the highest profit.
Below are some hotel's created by teachers during a session at the NS MTA conference in Oct. 2015.
Suggestions for Improvement
Resources Below are my Powerpoint introduction and a student handout. Also included is an analysis of several different hotels to see how their profits compare.
Why I Like This Task
Nova Scotia Curriculum Outcomes
EL
|
Categories
All
|
|||||||||||||||||||||||||||||||||||||






















 RSS Feed
RSS Feed