|
Yesterday I gave a presentation on self-checking math activities for the 2023 NCTM Virtual Conference. I find presenting at conferences valuable because it makes me reflect on my work and think deeply about why I'm selecting or creating certain activities for the classroom. I thought I was finished with my presentation when I saw a variation of a loop card activity that I decided to give a try. Loop cards make for a great self-checking math activity. In a "loop card" activity, the rectangular cards each have two values or expression on them, much like a domino. Students evaluate the expression on the right of side of the card and find a different card whole value on the left side is equivalent. These cards are then joined together (for example, x+3=7 on the right side of one card would join with x = 4 on the left side of another card). Students continue this way until a loop is created with the cards. For a nice example of loop cards, check out Don Steward's post at https://donsteward.blogspot.com/2015/02/loop-cards.html. The variation on this activity that I saw was NRICH's Doughnut Percents activity. In this activity, four students work as a team. Each student is given four cards and tries to make a small loop (for a total of 16 cards). They will typically not have the correct cards and need to trade cards with other members of the group. When complete, there will be four, four-cards loops created, one for each student. The twist with this activity is that the students have to do this quietly. They can just grab cards from other members of the group, but wait for the other student to give them a card that they need. It is very difficult for students to work together silently. I was inspired by this activity to give it a try with other classes. I created a "Derivative Donuts" activity and gave it a try with a Calculus class to review power, product, quotient and chain rules for derivatives. The google slides file can be found here: https://docs.google.com/presentation/d/1lMrJhNWY3jPCqlZrui8EBPe5YeCUdLxt3-akhkGwPxU/edit?usp=sharing. The cards are organized by loop in this file... with a larger group, I would mix the cards up and then have students cut them out... many hands make light work. I used the percent activity above to teach students the rules for the activity using content that they were confident with. Then I gave them the derivative activity which they found challenging. I thought that this activity was a nice change from a typical card sort or question stack type of activity. I like that students worked together as a team to try to create the loops. Because students weren't talking, one student wasn't able to dominate the team and take over the process. Each students had to participate for the group to be successful. The next time I try this activity, I'm going to try having teams of three students with five questions each. I think groups of three might be easier to form small groups (although I'll need more sets of cards). I also recently saw NRICH's Simplifying Doughnut activity which I'm looking forward to try with students. EL
In previous years, I've taught related rates in calculus class by the book. As in, we worked through the example problems from the textbook together and then students individually worked on the practice problems. After working through some examples, I would give students some more challenging problems as an assignment. Recently, a teacher reached out looking for some new ideas for teaching related rates. We brainstormed some ideas of how we could make related rates more engaging and hands-on. We decided to create some stations where students could experience and take measurements of related rates in action. It turns out, this is probably the reason that related rates problems are in our textbook. While doing some research to prepare this activity, I found an article titled, "The Lengthening Shadow: The Story of Related Rates" by Bill Austin, Don Barry and David Berman. This article is from Mathematics Magazine (Feb 2000, Vol. 73, No. 1, pp. 3-12). In this article, the authors state that related rates problems originated in the 19th century as part of a reform movement to make calculus more accessible. By observing changing rates, students would be able to measure concrete examples and discover their relationships. Joshua Bowman discusses how he grounded his teaching of related rates using observations in his blog post Using calculus to understand the world. Related Rates StationsFor this activity, we decided on four stations: Station 1 - Blowing Up a Balloon. Blow 5 big breaths into a balloon. After each breath, measure the circumference of the balloon and calculate radius and volume. How are radius and volume related? Station 2 - The Sliding Ladder. A metre stick is sliding down the wall. The bottom of the metre stick is moving away from the base of the wall at a constant rate. How fast is the top of the stick sliding down the wall? How are they related? Station 3 - Building Fences. Build several “fences” (rectangles made with multi-link cubes) such that the length is twice the width. Put them in order of size. Measure each rectangle’s length and width. What is the rate of change of the area? How are perimeter and area related? Station 4 - Driving Cars. Two toy cars are traveling at different rates in perpendicular directions. How fast are each of the cars travelling? How fast is their distance apart changing? How are they related? After taking measurements at each of these stations, students drew a picture and created an equation to relate the quantities to each other. We used implicit differentiation to determine the relationship of the rates and then we tested our equations with our collected data. Reflection and ResourcesThe activity went a bit long for one class period. Next time I would either split the activity up over two class periods or reduce the number of stations to three. This will allow more time to consolidate the learning at the end of the lesson. As Tracy Zager says, "never skip the close." If you're interested in giving this activity a try, below are the files I used: Related Rates Stations Google Slides Related Rates Recording Sheet Update - 13 AprilAfter doing this activity a few times in classrooms, I decided to reduce the number of stations from 4 to 3. In a 75 minute period, students were able to complete the three stations with a few minutes at the end to consolidate the lesson. I also changed the set up for the driving cars question to make it a bit more interesting. Here are the updated files that I've been using for 3 stations and a different problem for the driving cars problem. Related Rates Stations Google Slides Related Rates Recording Sheet Nova Scotia Mathematics Curriculum Outcomes Calculus 12 A3 - Demonstrate an understanding of implicit differentiation and identify situations that require implicit differentiation Calculus 12 B14 - Solve and interpret related rate problems EL
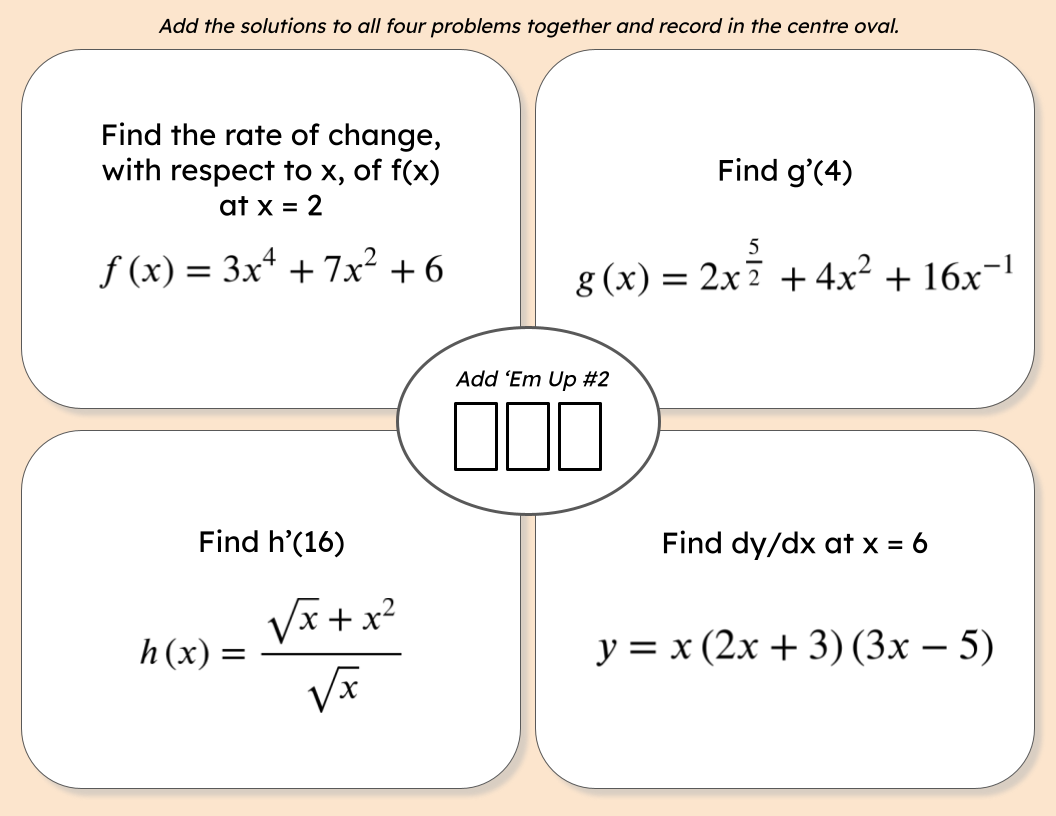
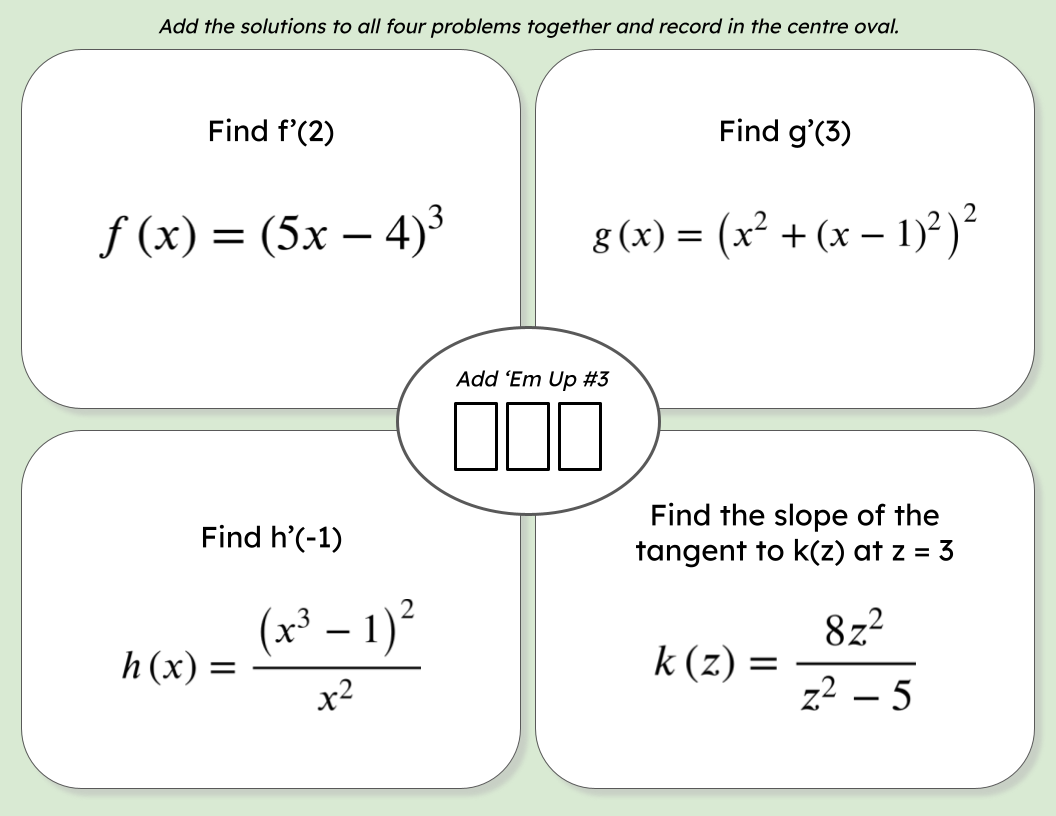
An "Add 'Em Up" activity is one where several problems are given and students sum the solution to come up with an answer. They can then check their answer to see if they have the correct total. If not, they can work to find their mistake. This "self-checking" activity lets students know there is an error but not exactly where to find the mistake. There are lots of different versions of this activity. You can vary the number of questions that students have to add together. The more questions there are, the more difficult it will be to find any mistakes they might have. I feel that the harder the questions are, the fewer should be in a set(3 or 4 questions in a set seems to be the sweet spot). You could have students work in small groups or individually. You can give students several sets of questions all at once or sequence them one at a time or as a stations activity. Below is an activity I recently did with a Calculus 12 class to review several different derivative rules: Derivative Rules Add Em Up Activity Each of these sets of problems was printed on a different colored paper and each small group of students started with sheet 1. When they had a solution for the sum of the problems on their sheet, I checked their answer. If they were correct, I gave them the next set of problems. If they were wrong, I told the to find their mistake. If they were struggling I could give them a hint on where to look for their mistake or guide them with some probing questions about their work. The colored sheets made it really easy to scan the room to see how far each group had progressed and focus my attention on groups that may need some additional support. In the past, I've just printed the sum in the middle of the page but I really like having the check in with students when they have finished each set of problems. Students checked their final sum on a box with a 3 digit combination lock on it. If correct, they could retrieve a piece of candy for each member of their group from inside and then relock the box for the next group. For some other examples of "add 'em up" or "sum it up" types of activities, check out these links:
EL
Auctions can be a fun and engaging activity in math class. The first auction I ever tried with a class was a unique bid auction that I learned about from Dan Meyer. I called it a "Lone Wolf" auction after seeing a discussion about this type of auction from Shawn Cornally. Students really enjoyed it and it generated some great discussions about strategies. We collected some data and were able to look at some displays to analyze the game. I haven't used many auctions as part of a mathematics activity. I was always concerned that too much time would be taken up by the logistics of the auction and there would not be enough time devoted to mathematical analysis. I learned some strategies for focusing on mathematical reasoning by reading how other teachers have facilitated auctions to make engaging math activities. Here are a few below: Function AuctionSarah Carter created a function auction activity for students to deepen their understanding of what makes a relation a function. Students bid on lots containing a variety of relations... some functions and some not. The team with the most functions at the end of the auction wins. Students work as a team to try to identify which lots contain the most functions and what a reasonable price for each lot might be given their starting funds. Sarah found this to be more engaging than a traditional function/not-function worksheet. The activity generates a lot of student conversation and discussion about functions. Dice AuctionNat Banting created a dice auction activity to get students thinking about the probabilities of outcomes when rolling two dice (this activity was won the 2020 Rosenthal Prize). In his description of the activity, Nat makes sure to include plenty of time for student teams to discuss their strategy and to try to assign a reasonable price to each event. He also builds in some reflection questions for students to answer at the end of the activity. This activity reminds me somewhat of the Borel Dice board game. Definite Integral AuctionI decided that an auction might be an engaging way for students to practice evaluating definite integrals in calculus class and so I created a definite integral auction activity. I incorporated some of the ideas from both Sarah's and Nat's auction activities. My auction is described below. As in Sarah's activity, I included time for students to talk and strategize by starting with five minutes to review the "auction catalogue". This page shows all the values that will be auctioned. As in Nat's auction, I scheduled in time at the halfway point for students to assess their situation and review the remaining lots. This gives students time to calculate their current integral and determine how they might increase its value even further. I also included some of Nat's reflection questions at the end to consolidate the activity. I got some additional ideas from Lola Morales (@lolamenting) when she posted on Twitter how she was going to use this activity in her classroom. If you have any tips or suggestions about auctions in math class, I'd love to hear about how you facilitate these types of activities. EL
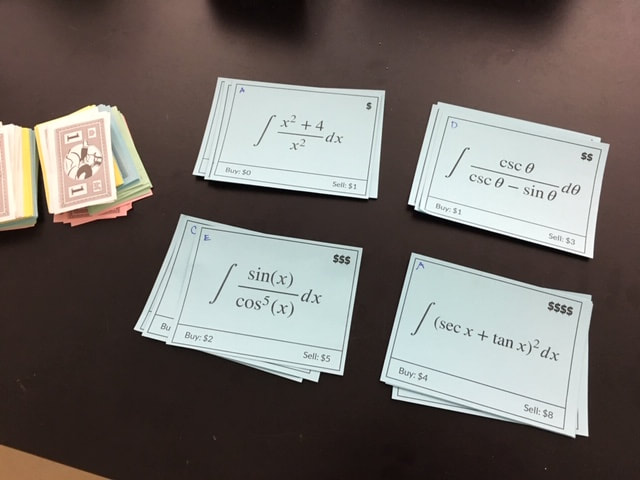
Some colleagues recently told me about an activity they had used in class called "Math Market". I'm not sure who originally created it. The teacher who shared it with me learned it at a math conference several years ago. I decided to give it a try with a Calculus class that was just finishing up a unit on integration. Here is how the activity is run. Students work in small groups (we had groups of three). Each group starts with $5 and selects a captain who can buy questions of different levels of difficulty from the market. Easier questions cost less and have a smaller profit. More difficult questions cost more and have a higher profit. The captain takes the purchased question back to their group to solve. Once they all agree on a correct solution, the captain returns to the market to sell the solution for a profit. The card is added back to the bottom of the market pile and some other group will have an opportunity to buy it. If their solution is correct, they buy a new question and continue working. If the solution is incorrect, they have to buy the question again to attempt a revised solution (or they can purchase a new question at a different level of difficulty). We decided to purchase the solution at a reduced price ($1 less) if they forgot to include the "+C" at the end for the constant of integration. The easiest questions were free so that if groups went bankrupt with an incorrect solution, they would still be able to "buy" another a problem. I printed the questions on coloured card stock and cut them out. Each question was marked with its level of difficulty. I also added a letter to the card so that it would be easy to find its solution to check the answers. Resources
How it WentI like that students got immediate feedback on their work. If it was wrong, they had to work with their group to correct their mistake. This was a test review for the class so there were lots of different types of problems mixed together and students had to determine what strategy would be best to solve each problem. It is a nice way to introduce some interleaved practice. This activity could be done with nearly any topic but it worked really well for integration as the questions were challenging and took them some time to solve. This made the market area less crowded.
I'm sure there are lots of variations of this activity. If you have some suggestions, I'd love to hear about them. EL
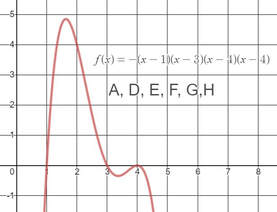
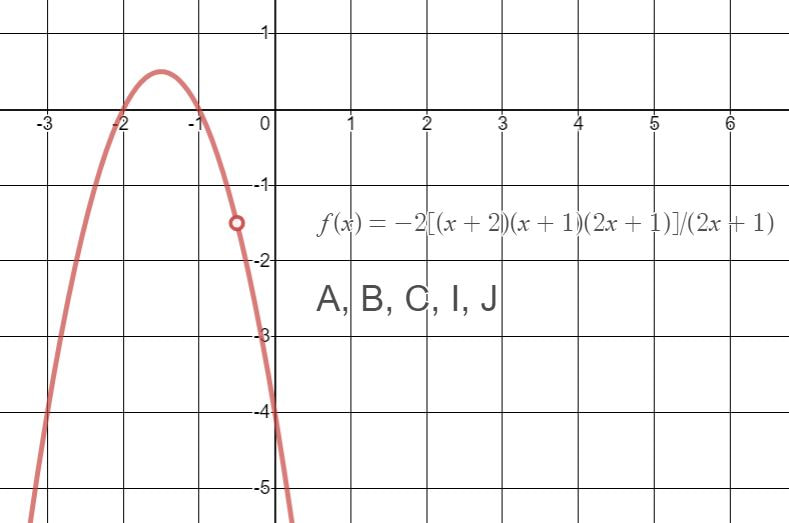
I recently attended Nat Banting's presentation at the Ontario Association for Mathematics Education annual conference in Ottawa (#OAME2019). He talked about "Creating Mathematical Possibility by Constraining Mathematical Possibility" (you can check out the slides from this presentation on his website). Last week I saw several educators sharing variations of a task that Nat presented on his blog called a 'menu task'. In a menu task, students are given a list of specifications and are asked to create functions that satisfy these specifications. It would be a fairly straightforward task for students to create a different function for each single specification (e.g. create a function that has a positive y-intercept). Students are challenged by asking them to use as few functions as possible to satisfy all the specifications in a list (in whatever combinations they desire). Amie Albrecht shared a Linear Relationships version of this menu task which inspired me to try creating one for high school calculus. Calculus Functions Menu TaskInstead of jumping right into the menu, I wanted to make sure that students were familiar with the expectation so I decided to build up to the menu. I started by asking students to come up with one function to satisfy each specification. Then I used the same specifications but asked students to satisfy them with only two functions. After getting used to the idea, I then continued with the Calculus functions menu task. The students have just started integration so this is mainly a review with just a bit of integration thrown in. If you'd like to give this task a try with your students, here is a link to my google slides. Example SolutionsHere are three example functions that I came up with to satisfy these ten specifications (some specifications are satisfied by more than one function): A,D,E,H) y = -(x+2)(x-1)(x-3) C,G,H) y = (x+2)(x)(x-2) A,B, F, I,J) y = -[(x+1)(x+1)(x-1)]/(x-1) Students were able to come up with fewer functions for this task. Here is one student's two functions to satisfy the ten specifications. EL
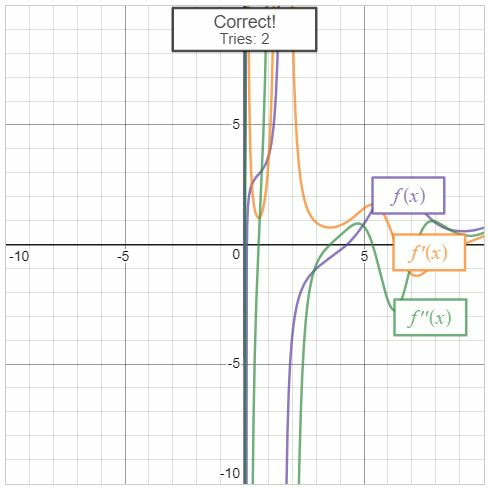
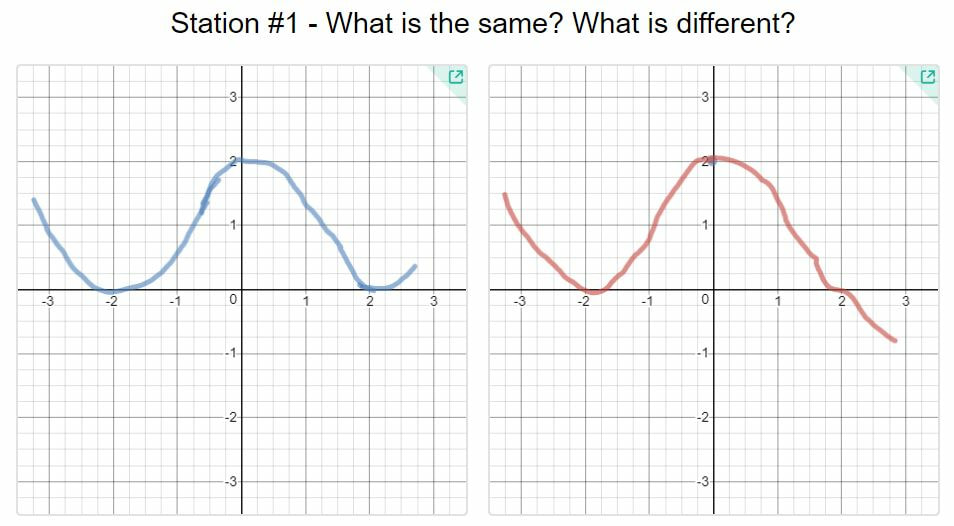
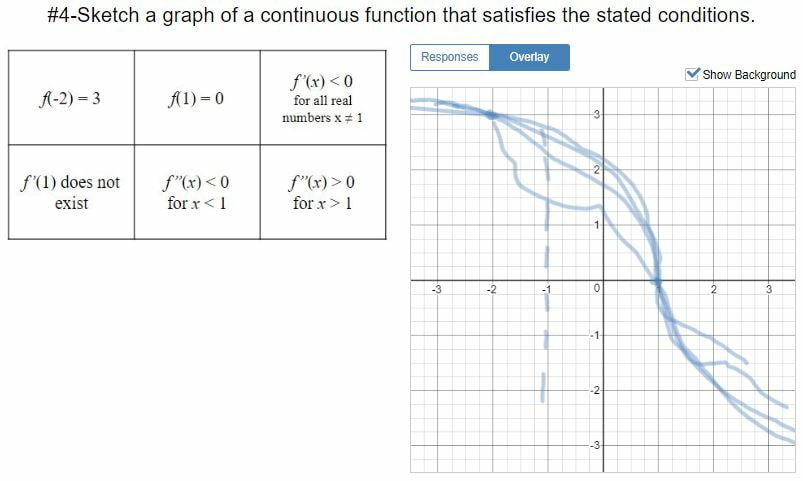
I recently had the opportunity to work with a calculus class on curve sketching and how derivatives affect the shape of a graph. The classroom teacher and I brainstormed some ideas about how we might infuse some hands on activity into the lesson. We decided to try an activity called Functions on the Floor. I originally saw an outline of this activity in a presentation from Liana Dawson called Hands-On Calculus Activities. Warm up - Functions and Their DerivativesWe started the class out with a Demos activity called Functions and Their Derivatives. We had students work in pairs on this activity. In the first part of the activity, students are presented with the graphs of three functions and they have to decide which is the original function, which is the derivative and which is the second derivative. In the second part of the activity, students create their own challenge and then get an opportunity to try out the challenges created by other groups. I really like the collaboration and discussions creating by working on these challenges. Functions on the Floor InstructionsAfter the warm up, we transitioned to the Functions on the Floor activity. We used masking tape to create several coordinate systems on the floor with the x- and y-axis labeled from -3 to 3. At each of these stations was a list of information about a continuous function. Students used a small rope to create a function on the axis that satisfied all of the conditions listed. They then drew their function into a Desmos activity I had prepared. Using the drawings in the Desmos activity we could monitor students activity and plan for our review of the functions at the end of class. We heard some really constructive conversations taking place. The Google slides for the stations can be found here. Sharing our WorkI thought that this activity was a nice way to incorporate both hands-on physical problem solving while still leveraging some of the power of online tools like Desmos. I learned a few lessons doing this activity and the classroom teacher and I had a productive discussion after the lesson. We talked about how the lesson went and where we saw areas for improvement. We both agreed that eight stations was more than needed as it took some time for the discussions in the student groups to come up with a reasonable graph. We thought that some of the stations could have fewer constraints to consider as well. Also, I think next time I would use something besides rope. I had pretty inexpensive rope and it wasn't as pliable as I would have liked. I think a thick piece of yarn might have worked just a well. If you give this activity a try, let me know how it goes. Nova Scotia Mathematics Curriculum Outcomes Calculus 12 B15 - Demonstrate an understanding of critical points and absolute extreme values of a function Calculus 12 B16 - Find the intervals on which a function is increasing or decreasing Calculus 12 C5 - Apply the First and Second Derivative Tests to determine the local extreme values of a function Calculus 12 C6 - Determine the concavity of a function and locate the points of inflection by analyzing the second derivative EL
|
Categories
All
|




























 RSS Feed
RSS Feed