|
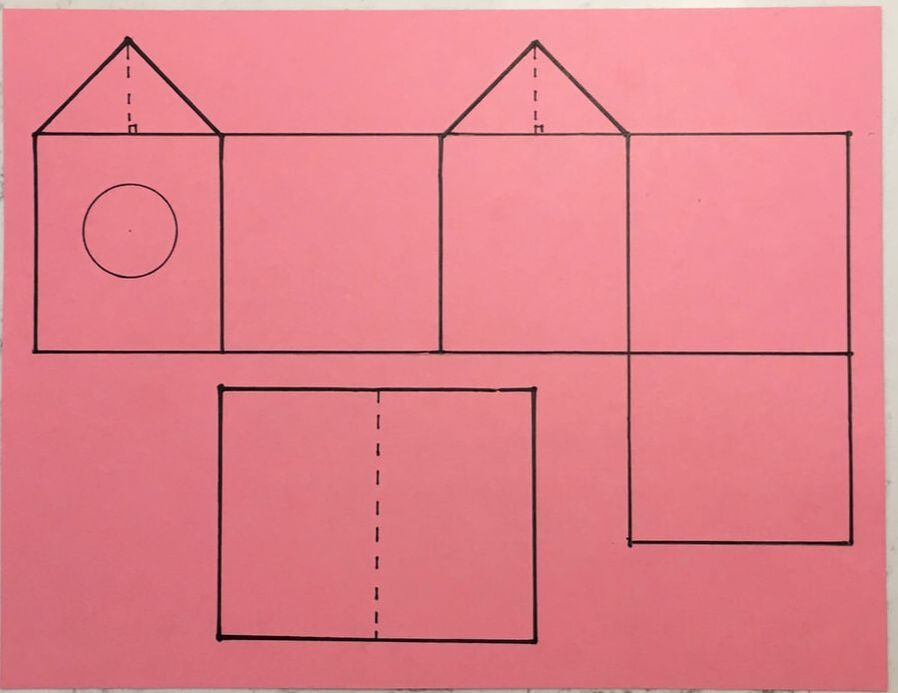
"Design and build a model birdhouse from a single sheet of 8.5" x 11" sheet of paper." This open ended activity seems simple at first but will require careful planning and attention to detail for students to be successful. You might start off this activity by showing a photo of an actual birdhouse and asking students to brainstorm the features of a good birdhouse. A website like this one might be a good guide. Next you can talk about the expectations for their model birdhouse design:
Students should then be asked to create a design. The design should minimize wasted paper (i.e. use as much of the page as possible) and be easy to assemble (i.e. minimize the number of pieces you have to cut out and assemble). You can then show students an example of a finished design. ProcedureStep 1 - Students should brainstorm some possible designs (at least two) on a piece of looseleaf Step 2 - Ask students to pick their favourite idea and share it with the teacher Step 3 - Once the teacher approves their design, students are given a piece of card stock. They can then lay out their design with a ruler Step 4 - When finished, students will measure and record all dimensions for their model. Students then calculate the surface area and volume of their design Step 5 - The final step is to cut out and assemble their birdhouse model! Here is a Google slides document that could be used to introduce the activity to students and make the expectations clear. Math at Work 10 Activity: One teacher modified this activity by giving students a selection of designs to choose from instead of designing their own (here are links to pdf template 1 and template 2). Students then did all of the measurements and computations and had to determine costs for shingles on the roof, siding for the walls and paint for the interior. Here is a handout similar to the one she used. Extensions: If you were to take your model and use it to build an actual birdhouse from wood, what would have to change? By what scale factor would you have to increase the size? How would building with 3/4" thick wood (instead of flat paper) change the size of the pieces needed? What supplies would you need and how much would it cost to build? NS Outcomes: Mathematics 9 - G01 Students will be expected to determine the surface area of composite 3-D objects to solve problems Mathematics 10 - M03 Students will be expected to solve problems, using SI and imperial units, that involve the surface area and volume of 3-D objects, including right cones, right cylinders, right prisms, right pyramids, and spheres. Mathematic at Work 10 - M04 Students will be expected to solve problems that involve SI and imperial area measurements of regular, composite, and irregular 2-D shapes and 3-D objects, including decimal and fractional measurements, and verify the solutions. Mathematics Essentials 12 - 2.4 Sketch and construct a model which will enable a student to show others some mathematics involved in a career interest EL
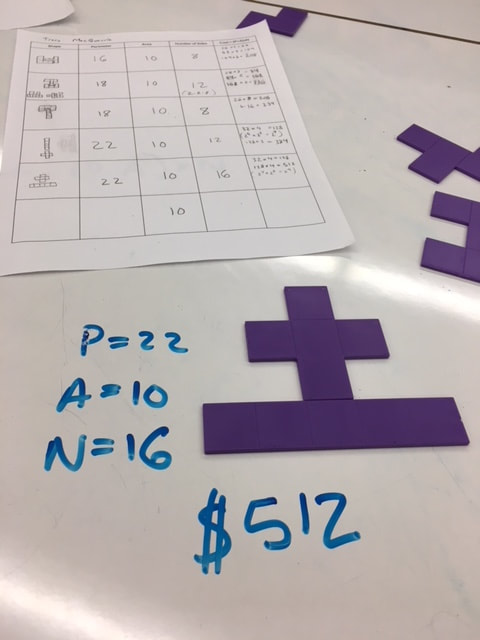
An engaging puzzle with simple instructions is to ask students to create a rectangle using pentomino pieces. Let them figure out what rectangle dimensions are possible given the total number of squares in the pentominoes they're using (for a full set of 12 pentominoes, 3x20, 4x15, 5x12 and 6x10 are possible). You can also print off a variety of other shapes and challenge students to fill those shapes with pentominoes or have students create their own shapes and challenge their friends to solve them. Younger students can be challenged to fill an empty picture frame or tray with pentominoes. Here are five great games, puzzles and activities (in no particular order) that use pentominoes:
2. Pentomino Puzzles from Jon Orr (@MrOrr_geek) - Jon describes an activity where students are given a hundreds chart and a transparent pentomino. Ask students to place their pentomino on the hundreds chart so that it covers a sum of 135. Then ask students to share their strategies for finding the correct placement. Are there sums that are not possible to achieve? Continue the activity by selecting different tiles, giving different sums to find, creating equations and solving them. I also saw these questions posted by Amie Albrecht (@nomad_penguin) on twitter, "Can you find a pentomino that covers numbers that: sum to 150, sum to an even number, covers three multiples of 4, and more". Jon created an online Desmos Activity that allows you to do this activity virtually. 3. Pentomino Farms - I was introduced the the pentomino farms activity from Martin Gardener's book Knotted Doughnuts and Other Mathematical Entertainments. The task is to use the 12 pentominoes to build a fence around a field on your farm. The rule used to join the pentominoes to form a fence is that they must touch along the full edge of a square and not just at the corners. There are four types of farms to create. For each type, what's the largest field you can enclose?
4. How Convex is a Pentomino? - Which pentomino shape is the most convex? How do you measure "convexity"? This is an interesting question that generated lots of discussion on Twitter. Some interesting methods of measuring this were discussed by Alexandre Muñiz (@two_star) in his blog post, "Vexed by Convexity." I think it would make a great discussion for students to rank the pentominoes by convexity and then defend their choices.
If you have a favourite activity, puzzle or game featuring pentominoes, I would love to hear about it! EL
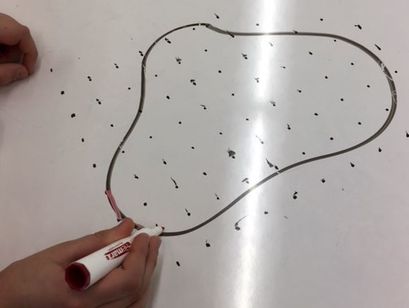
I prepared a lesson plan to work with a student. I carefully considered how I would introduce the topic, the path that the lesson might take and the questions that I would ask to prompt our discussion. I thought about the manipulatives that we might use to visualize and physically interact with the problem. I had a course carefully laid out. I started by drawing an irregular, kidney shaped area on the desk and asked the student how he would estimate the area of the shape. I was prepared for a number of different responses that I thought I might hear... but the student didn't follow my carefully plotted course for our lesson. Instead he replied, "I'd use Pick's Theorem." I grew up sailing on the Columbia River. When changing course on a sailboat, you can either turn the bow (the front of the boat) through the wind (i.e. tacking) or you can turn the stern (the back of the boat) through the wind (i.e. jibing). When tacking, the boom gently moves from from one side of the boat to the other. Jibing on the other hand can be dangerous as the boom suddenly jumps to the other side of the boat. When the student suggested Pick's Theorem, it felt like changing course by jibing instead of by tacking.
After our excursion through Pick's Theorem we found our way back to estimating the area with some manipulatives. First we covered the shape with square tiles and then we covered the shape with pennies. We found that we could cover the shape with 66 square tiles. I asked the student how the area we found with Pick's Theorem and the area we found with square tiles compared. Through our discussion we decided that we needed a common way to talk about these areas so we converted both to square centimeters. We found that the area from Pick's Theorem was 382.5 cm^2 and the area using square tiles was 412.5 cm^2. Next, we looked at our penny solution. We looked up the diameter of a penny online and found that 135 pennies at 2.85 cm^2 each gave us a total area of 384.75 cm^2. While discussing how this estimate compared to our others, the student started talking about Alex Thue and his theorem on circle packing (this student has a really good memory). The student remembered that the efficiency of hexagonal packed pennies was about 91%. So we used this efficiency to correct our penny estimate to make it even better. This led to another discussion that I hadn't planned on about tesselations and polygons that tile the plane. The student said he had read in a book that there were 14 irregular pentagons that tile the plane. His book was a few years old however so he didn't know that a 15th pentagon had been discovered in 2015 or other recent work in this area. While the lesson didn't go quite as I had planned, I was really happy to be able to take the student's contributions to the discussion and weave them into the overall narrative of our work. Being flexible, listening to students and incorporating their contributions into a discussion can sometimes throw you off course and you might end up someplace unexpected. The journey along these altered courses however can be incredible. EL
|
Categories
All
|








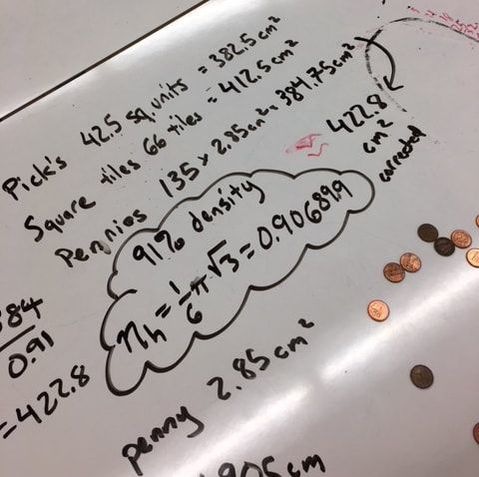
 RSS Feed
RSS Feed