|
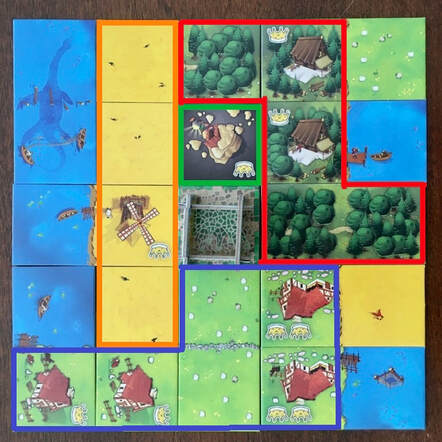
Working from home and looking after an 8 year old at the same time throughout the past three months has proven to be complicated. Providing an enriching, engaging and educational home environment for my son while still attending to work deadlines and schedules has been a difficult balancing act. A provincial state of emergency required us to adapt our daily routines. One positive change has been playing board games. My son and I have played daily board games and card games. We have gone from simple children's games such as Snakes and Ladders to more complex European-style board games like Alhambra. Our favourites (and most played) games have been: Splendor, Tiny Towns, and Kingdomino. These games give players lots of opportunities to use spatial and numeral reasoning to make informed choices. These games all work well as two player games or with larger groups. Playing KingdominoA game that I have come to appreciate is Kingdomino. It is easy to learn, quick to play and has complex strategy. In this game, players take turns drafting domino shaped tiles to add to their kingdom. Players have to build within a size constraint. Players start with a 1x1 home castle tile and your kingdom, including this home tile, can not exceed 5x5 (meaning you can add a maximum of 12 tiles to your kingdom). This size constraint means that if your kingdom is not well planned, you might end up with empty spots that can't be filled. The goal is the maximize the value of your kingdom at the end of the game. To calculate the final value, you multiply the area of each contiguous region of a single terrain type by the number of crowns contained in the region (there are six different terrains types: pastures, wheat fields, lakes, mines, forests, and swamps). If a region doesn't have any crowns in it, it scores zero points (e.g. there is a region of 4 lakes in the kingdom below but because it has zero crowns, it scores 4x0=0 points). There are four different regions with crowns in the kingdom below. The wheat field (outlined in orange) scores 4x1=4 points. The pasture (outlined in blue) scores 6x6=36 points. The forest (outlined in red) scores 5x2=10 points. And finally, the mine (outlined in green) scores 1x1=1 point. This gives a total values of 4+36+10+1=51 points... a decent total score. Bringing Math to the SurfaceWhen I first looked at the mathematics applied in this game, I only considered adding up the scores to determine a winner at the end. Playing this game with my son however led me to see how mathematical decision are used throughout the game. Each turn, you must decide which domino (or dominoes if you're playing with two people) you will select for your kingdom. In order to bring mathematical reasoning to the surface, I began reasoning out loud. This let my son hear all the considerations that go into my selection. Given the growing kingdom below, which of the four dominoes would you select and why? The first domino doesn't have any crowns, but it could be added to the bottom of the kingdom to make a region of 4 wheat fields where crowns could be added on a future turn. The first domino also gives me the benefit of going first next turn (dominoes are placed in order from top to bottom each turn). The second domino has a crown in a forest. This could be added to existing region of 3 forest that has 2 crowns already. This would turn your forest region from scoring 3x2=6 to 4x3=12... a gain of 6 points. The third domino would be even better. Playing it in the bottom right would still gain you the 6 points in the forest region but also turn your 2 point lake region in to a 3 point lake region. The last domino could add a crown to your lake region and a space to your forest region. This would make the forest region worth 8 (a gain of 2) and your lake region worth 6 (a gain of 4). Looks like the third tile would give us the most immediate gain in score (a gain of 7). ProbabilityOlder players will also need to consider the unequal distribution of terrain types and crowns. There are lots of wheat fields (26) but only 5 have a single crown. There are 14 pastures but two of these have one crown and two have double crowns. Mines are rare with only 6 of them in the game but they can generate big scores. Three of the mines have double crowns and one mine has the only triple crown in the game. The trick is to grab them when you can and place them next to each other. Strategy vs. LuckThere is a fair amount of luck in this game. The dominoes are shuffled and show up in random order. If you have the first pick in the round you can get a great tile but if you go last, you may get stuck with a tile that you don't really want. Also, if you're not playing with four players, you won't be playing with the full set of dominoes. A domino you were hoping to get might not even be in the game. With that being said, there is enough strategy to keep both kids and adults thinking critically about their decisions throughout the game. Playful MathI think this is a great example of a board game that demonstrates a playful and entertaining way to practice mathematical skills and reasoning. It's easy to learn rules and quick play time make it a great choice for playing with younger family members. It has been in regular rotation with my family during our at home learning. If you want to quickly learn how to play Kingdomino, you can watch Rodney Smith's Watch It Played video on YouTube. I have come to appreciate how much skill there is to teach an 8 year old, with limited patience, the rules to a new board game. If you want some tips on teaching your kids (or friends) how to play a new game, I highly suggest Shut Up & Sit Down's video How to Teach Board Games Like a Pro. A lot of these tips apply equally to the classroom and teachers will be able to see how good pedagogy is universal. EL
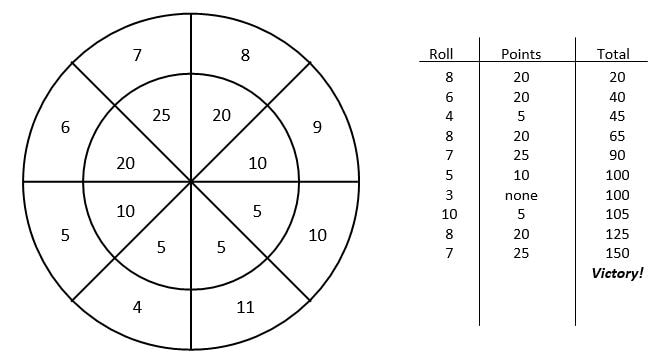
Below is a simple probability game that I've played with students for many years in a number of different courses. I don't really remember where I got it from but if you've seen it before, I'd love to know where it originated. I've found that students enjoy it and they really develop some good ideas about probability. Its similar to the Two-Dice Sum Game from Marilyn Burns but with some additional mental math for older students. InstructionsThis is a game for two or more players. Each player creates their own score card by drawing two concentric circles and then divide it into eight sectors. Choose eight different numbers between 2 and 12 and place them in the sectors in the outer ring. In the inner ring of the circle place numbers that add up to 100 (it is easiest to stick with multiples of 5). Roll two dice and add the numbers together, if the total is one of the numbers in the outer ring of your score card, you score that numbers value (the number in the inner ring). Players alternate rolling and scoring on their card until one of the players has 150 or more points (or to 100 for a bit shorter game). A google doc handout for this is available here. Sample Score CardTypically, the first time students play, they will randomly select numbers and values for each sector. After students have had the chance to play a few games, stop and ask them to look at different score cards to see if there any common characteristics of winning cards. What makes a good score card? Is it all just luck or are some cards better than others? Developing a StrategyWhat makes a good score card? Here are some common student observations:
Experimental ProbabilityYou might ask students to roll two dice a bunch of times and record which numbers come up each time. Create a bit dot plot or a bar graph at the front of the classroom using all of this data. Ask students to predict what the shape of this graph will be. You could also use an online tool to model lots of dice rolls to see how it compares to the class data. You could then discuss the theoretical probability for each sum and compare it to the data you gathered. I always find this a fun activity and a nice way to start a discussion about probability and strategy. A nice question to start the class on the following day would be a Would You Rather? math prompt, "Would you rather flip 2 coins and win if they match OR roll 2 dice and win if they don't match?" Another great follow up activity would be Don Steward's Dice Bingo. Nova Scotia Mathematics Curriculum Outcomes Mathematics at Work 12 P01 - Students will be expected to analyze and interpret problems that involve probability. Mathematics Essentials 10 G4 - Compare predicted and experimental results for familiar situations involving chance, using technology to extend the number of experimental trials. Mathematics 8 SP02 - Students will be expected to solve problems involving the probability of independent events. Mathematics 7 SP06 - Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. EL
Coins in a Row is a simple game that I have used in lots of classrooms at different grade levels. It is a great way to tackle some mental math and logical reasoning. I first learned about this game in an article from Ivar Peterson's Math Trek. The game originally appeared in Peter Winkler's Mathematical Puzzles: A Connoisseur's Collection (2004). The Rules: Arrange a bunch of coins of various denomination in a row (any even number of coins will do). The first player chooses a coin from one of the ends and slide it over to her pile. Your opponent then chooses a coin from one of the ends of the row of remaining coins. You and your opponent take turns removing a coin in this manner until they are gone. The player with the highest total value of coins wins. The fun part of this game is that it is unfair. Unfair games are a great way to get out of doing some chores while you're visiting in-laws over the holiday break (e.g. "Lets play a game, the loser has to wash the dishes"). The player who goes first can always win if they know the correct strategy. After playing this game a few times, I let students know that it is an unfair game and ask them if they can find a winning strategy. Here is how the winning strategy works. Label the coins from 1 to n going from left to right. Add up the value of all the odd labeled coins then add up the value of all the even labeled coins. The first player can choose either an odd or even labeled coin. The second player only has two evens to choose from if the first player took the first coin from the row. The second player only has two odd coins to choose from if the first player to the coin from the end of the row. The first player then just takes a coin from whichever end the second player chose from and the first player can guarantee that they get either all the odd or even labeled coins. This strategy guarantees at least a tie for the first player. It is not necessarily the "best" strategy however. According to Ivars Peterson, no one has yet worked out an optimal strategy that works for any number of coins.
Alternate versions are quite easy to create for this game. For example, Coins in a Circle. In this version, the first player can pick any coin, then play continues as in the previous version. Another way to play would be to use a deck of cards (remove the face cards) and deal out 10 cards in a row. EL
|
Categories
All
|
||||||||


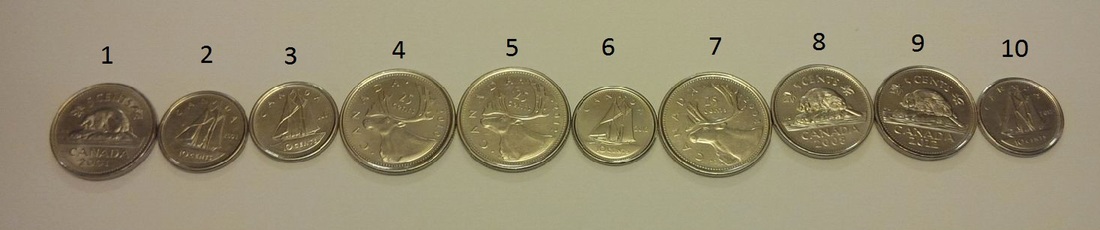
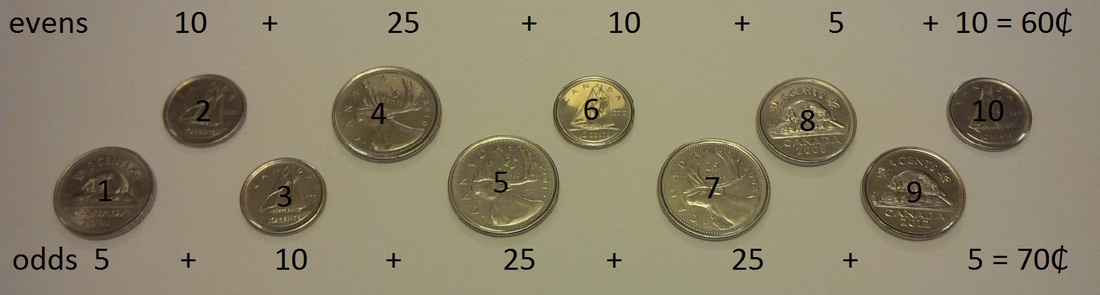

 RSS Feed
RSS Feed