|
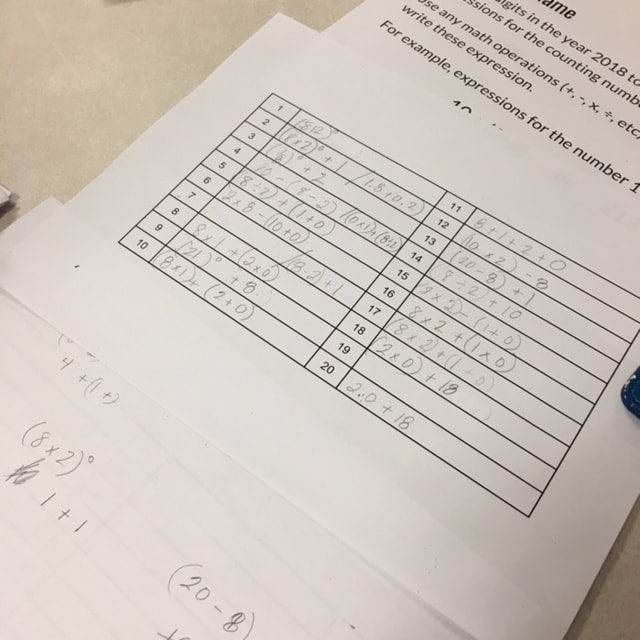
During a professional development session today with grade primary to grade 9 math coaches and support teachers, we spent some time working on solving some math puzzles. We used our work on these puzzles to reflect on what good group work looks and sounds like. We also discussed the characteristics of effective mathematical communication. It was great to see positive energy and teachers supporting and encouraging each other. Below are the five math puzzles and investigations that we worked on. We selected these puzzles because they are easy to explain, open to a wide range of students, and offered a fun challenge. 1-10 Card InvestigationThis problem from Marilyn Burns asks you to find a special order for a stack of cards, Ace through 10. Place the stack of cards face down and turn over the first card. It should be the Ace. Place the next card on the bottom of the deck and then reveal the top card. It should be the number 2. Continue placing the next card on the bottom of the deck and then revealing the top card until all the cards are revealed. The face up cards should now be in order from Ace to 10. Marilyn recorded a video to demonstrate these rules that is much easier to understand than my written instructions. Marilyn's has a description of this problem on the MathSolutions website. This logic problem doesn't rely on any prerequisite mathematical knowledge and you can try it out quickly to see if you've come up with the correct solution. It gives students a chance to work together to try out strategies. The Square-Sum ProblemCan you order all the numbers from 1 through 15 so that the sum of any two consecutive numbers are always a square number? For example, in the sequence: 4, 5, 11; 4+5=9 and 5+11=16.I really like this problem because there are some great extensions to take this problem farther and there is a very nice way to visualize the possible solutions. Numberphile has recorded a great video demonstrating both the problem and solution. The Year Game - 2018Use the digits in the year 2018 to write mathematical expressions for the counting numbers 1 through 100 (we only went to 20). Use any math operations (+, -, x, ÷, etc) and parentheses to write these expression. There is a more detailed description of this problem at the Math Forum website. For example, expressions for the number 1 might be: 10 ÷ (2+8) or 218^0. This problem is very similar to the classic Four Fours problem but with new digits each year. Which numbers are the hardest to find an expression for? Why do you think this is? I think this problem also leads nicely to a discussion about mathematical elegance and beauty. Look at a variety of expressions with the same value. Which expression do you think is the best? What makes for an "elegant" solution? Perimeter 12This problem challenged groups to make as many different shapes as possible with a perimeter of 12 units using a geoboard (or dot paper). Shapes were recorded on dot paper to make sure no shapes were repeated as reflections or rotations. I've seen variations of this problem in several places. One of them is Brian Bolt's book Mathematical Activities (1982). He suggests not only to find shapes with a perimeter of 12 but to also find the area of each shape. You can then find which shape has the maximum/minimum area. He also challenges students to find non-rectangular shapes (e.g. triangles) with a perimeter of 12 units. There were some good discussions about the lengths of diagonal line segments on the geoboard. Eight DominoesThis problem is from NRICH. Finding a solution took some perseverance but most groups were eventually successful. The problem challenges you to create a square using 8 specific dominoes (0-1, 0-2, 0-3, 0-6, 1-2, 1-4, 2-2, and 3-5). In the 4 x 4 square, each of the columns and rows should sum to 8. The 3-5 domino seemed to be key as the rest of the squares in that row (or column) had to be blank. What are your favourite math or logic puzzles? EL
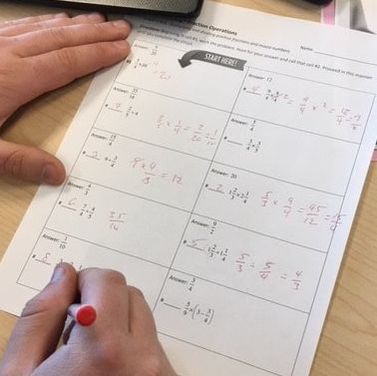
I'm a fan of self-checking math activities. These activities give students immediate feedback and help them to find and correct errors. Many students will be able to correct their own computational errors, especially if students are working in pairs or small groups. When students are unable to fix their errors due to more serious misconceptions, the teacher can step in to help develop understanding. This helps the teacher use their time efficiently and focus on students facing challenges. I've recently seen one math activity used in a number of classrooms in a variety of forms. I'll call this activity a "question chain" although I've seen it referred to using lots of different names. This activity starts with a set of questions and associated answers. Students start by solving one of the questions. The answer to this first question leads the student to the next question. This process is repeated until the student arrives back at the starting question. The answers form a "solution bank." If the student can't find their answer, they know that they've made a mistake and need to find and correct their error. Below are three different ways that I've seen this activity implemented in classrooms. Questions on Cards
Links: Questions Posted on the Wall
Links: Questions on a Worksheet
Selecting a MethodDuring a recent professional development session with math teachers, we tried this activity using all three methods. Participants were split into three groups and each group was given a different method. All three versions of the activity included the same ten questions (see the files below).
After completing the activity we had a discussion to compare the three methods. All of them took about the same amount of preparation and could be quickly created using questions from a textbook or other problem bank. How would students record their work in each method (on paper, mini-whiteboard, etc.)? How would the teacher assess students work in each method? Would each method work better individually, in pairs or in small groups? How might this activity be used in a combined grade classroom? Which method might be most culturally relevant for your students and how does your knowledge of your students inform your selection of a method? Which method is the most engaging for your students? We had a very productive and rich discussion. Have you used this type of activity in your classroom? Another variation of this method is the "I have/ who has?" oral classroom activity. Have you used a different variation of any of these methods in your class? Do you have a favourite method? Why is it your favourite? EL
A few colleagues and I recently initiated a bit of self directed professional development. We decided to watch a selection of math ignite talks as a focus for discussion regarding mathematics instruction and educational practices. In preparation for this, I reached out the the #MTBoS on Twitter to ask for suggestions. I was pleased to get some valuable feedback. We took the feedback we got from our Personalized Learning Network (PLN) as well as sharing our favourites with each other to create a playlist of math ignite talks. A big thanks goes out to The Math Forum at NCTM for having such a well organized and easy to access YouTube channel containing math ignite talks from numerous conferences. What are your favourites?
Has watching these videos inspired you to create your own mathematics ignite talk? If it has, and your looking for advice, look no father than Robert Kaplinsky's web page. He has a post titled, "How I Prepare for an Ignite Talk" that will provide you will lots of tips and ideas. Update: I've added a part 2 playlist of six additional math ignite talks here. EL
|
Categories
All
|
|||||||||||||||||||||||||||||||||||||||

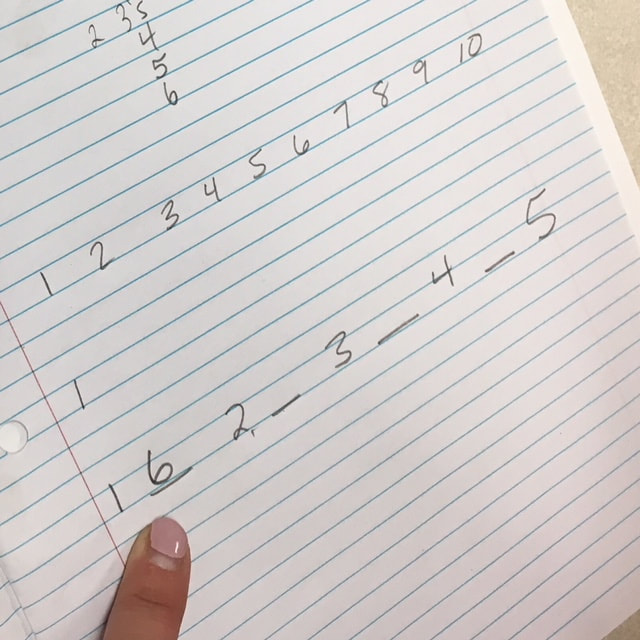


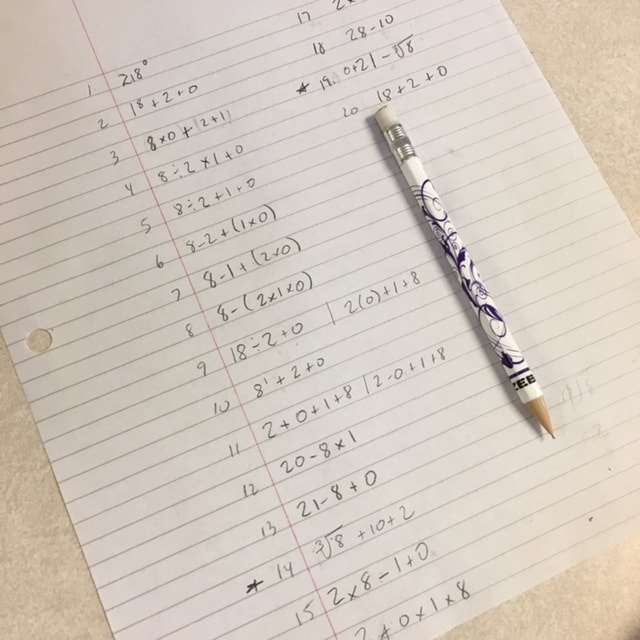






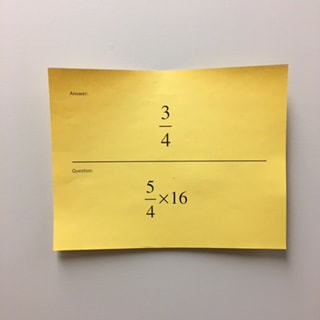






 RSS Feed
RSS Feed