When I got home, I did a search to find out why the machines were gone and ran across a story from Global News. It turns out that TD Bank had decided to retire all the coin counting machines in Canada in the wake of reports from the U.S. that the machines were short-changing customers. In a segment on the Today Show called 'Rossen Reports', a team investigated the accuracy of a number of Coinstar machines as well as coin-counting machines at various branches of TD Bank. The team tested the accuracy of the machines by carefully preparing bags filled with exactly $300 worth of pennies, nickles, dimes and quarters. They then used the machines to see how close their count was to $300. The Coinstar machines all checked out with the correct $300 total. The TD Bank machines did not fare so well. The totals on the machines tested at 5 different branches were: $299.95, $299.47, $299.30, $296.27 and $256.90. None of the machines returned an accurate $300 count. I don't think that machines can really be "100% accurate" all the time. What level of accuracy do you think is acceptable from a coin-counting machine? How much time does it take to roll $300 worth of coins and how much is your time worth? I would probably accept $299.95 for the convenience of not having to roll that many coins. I would be a bit more hesitant to accept $296.27 and definitely would not accept $256.90. While the TD Bank machines were free for customers, in Canada, Coinstar machines apply a coin counting fee of 11.9 cents per dollar. For the $300 counted in this test, the fee would have been $35.70. That is a pretty hefty fee. Questions and EstimationsAccording to a class action lawsuit filed in New York in April 2016, TD’s coin-counting machines processed 29 billion coins in 2012. Based on this figure and the data collected by the Rossen Report, how much money do you think customers lost? What factors did you consider when making this estimate? How would you design an experiment to test the accuracy of TD's coin counting machines? Would you test lots of different machines or a few machines multiple times? How many trials would you run to be confident in your results? What factors might contribute to the errors discovered in these machines? Nova Scotia Mathematics Curriculum Outcomes Mathematics 11 S02 - Interpret statistical data, using: confidence intervals, confidence levels and margin of error. Mathematics 11 S03 - Critically analyze society’s use of statistics. Grade 9 SP03 - Students will be expected to develop and implement a project plan for the collection, display, and analysis of data by: formulating a question for investigation; choosing a data collection method that includes social considerations; selecting a population or a sample; collecting the data; displaying the collected data in an appropriate manner; drawing conclusions to answer the question. Grade 7 SP06 - Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. EL
 https://www.ted.com/ https://www.ted.com/ I am trying to be purposeful and organized in taking the "Calls to Action" from the recent NCTM conference in San Francisco. I am going to play with "Deleting the Texbook" over my next few blog posts (watch Meyer's most recent NCTM presentation here for elaboration). Since I attended my first conference about 7 years ago, I have been heavily influenced by the work of Dan Meyer. His Ted Talk "Math Class Needs a Makeover" really changed the way I thought about teaching math.  I want to share something I did with first as a math coach with a class of grade 3 students and then as a presentation for teachers at the Nova Scotia MTA conference a few year back. I feel like I have been taking this particular "Call to Action" for many years now; I am excited about the evolution of this thinking and I wanted to show how I started with this work. The students in this class were a few weeks out from writing a provincial math assessment. The classroom teacher wanted to do some questions from the practice booklet. This was the original question:  Instead of posing the question as is, I took out as much information as possible while keeping the math I wanted the students to learn in mind. The students needed to get curious before I hit them with the math. All staff at schools need to wear an ID badge and laynard (wait for it...it will make sense in a moment). Lots of people keep keys, change, notes, etc in the plastic badge holder. Instead of asking the above question, I announced to the class that I had some change in my ID holder (I put the correct amount in and shook it for dramatic affect!). Their job was to figure out how much money I had. They were a little confused at first, so I prompted them; I told them they could ask me questions about the coins. I gave them a few minutes to think, then to confer with a partner before I took questions from the class. I recorded and answered their questions. Here are the questions they came up with along with my answers in brackets:
Each time I took a question, I asked students "Why do you want to know that?" or "How will that information help you solve the problem?" Once they had all the information they felt they needed, they set off to solve the problem. They basically constructed the original question on their own. And because they had a part in building it, they really understood the context of the problem and had ideas of how they might solve it. When they were confident that they had the solution, I let them empty my ID badge and count the coins. That is much more satisfying than just giving the correct answer. Students got to prove that they were right, rather than the teacher being in charge of all the answers. I often hear from teachers that their students don't understand word problems and that it's not the math, it's reading comprehension. I see this strategy of building a question with the class as a way to help them get inside the problem before they start. Another reason I like this strategy so much is that I was able to create it by modifying a resource (practice booklet) that I already had. We can get bogged down trying to find appropriate resources for students at appropriate levels. By using a resource I already had, taking out parts, and layering them back in as needed I was able to differentiate on the fly. No tiered lesson plan, no separate handouts. It was one problem that we worked together as a class to first build, then solve. The Most Interesting Question I Almost Overlooked"What kind of coffee do you drink?
I didn't understand where the student was going with the question but I asked the usual questions of him: "How will that help you solve the problem?" and "Why do you want to know?" The student thought I probably kept my coffee money in my ID badge. If he knew the coffee I drank, he would have the problem solved.** Based on his question, we created a series of extension questions to keep the problem solving going. **All Canadians know the price of a medium double double. :P KZ Coins in a Row is a simple game that I have used in lots of classrooms at different grade levels. It is a great way to tackle some mental math and logical reasoning. I first learned about this game in an article from Ivar Peterson's Math Trek. The game originally appeared in Peter Winkler's Mathematical Puzzles: A Connoisseur's Collection (2004). The Rules: Arrange a bunch of coins of various denomination in a row (any even number of coins will do). The first player chooses a coin from one of the ends and slide it over to her pile. Your opponent then chooses a coin from one of the ends of the row of remaining coins. You and your opponent take turns removing a coin in this manner until they are gone. The player with the highest total value of coins wins. The fun part of this game is that it is unfair. Unfair games are a great way to get out of doing some chores while you're visiting in-laws over the holiday break (e.g. "Lets play a game, the loser has to wash the dishes"). The player who goes first can always win if they know the correct strategy. After playing this game a few times, I let students know that it is an unfair game and ask them if they can find a winning strategy. Here is how the winning strategy works. Label the coins from 1 to n going from left to right. Add up the value of all the odd labeled coins then add up the value of all the even labeled coins. The first player can choose either an odd or even labeled coin. The second player only has two evens to choose from if the first player took the first coin from the row. The second player only has two odd coins to choose from if the first player to the coin from the end of the row. The first player then just takes a coin from whichever end the second player chose from and the first player can guarantee that they get either all the odd or even labeled coins. This strategy guarantees at least a tie for the first player. It is not necessarily the "best" strategy however. According to Ivars Peterson, no one has yet worked out an optimal strategy that works for any number of coins.
Alternate versions are quite easy to create for this game. For example, Coins in a Circle. In this version, the first player can pick any coin, then play continues as in the previous version. Another way to play would be to use a deck of cards (remove the face cards) and deal out 10 cards in a row. EL
|
Categories
All
|
||||||||||


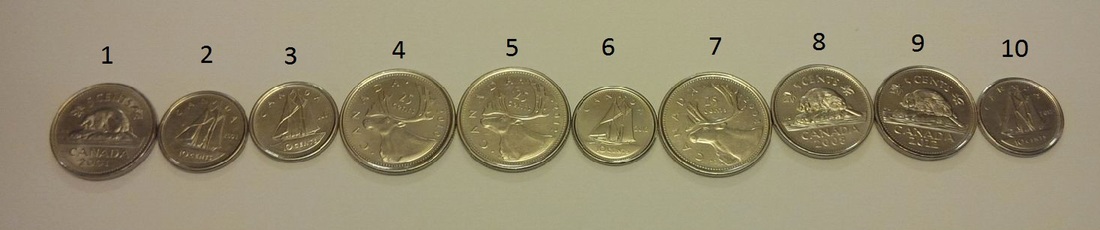
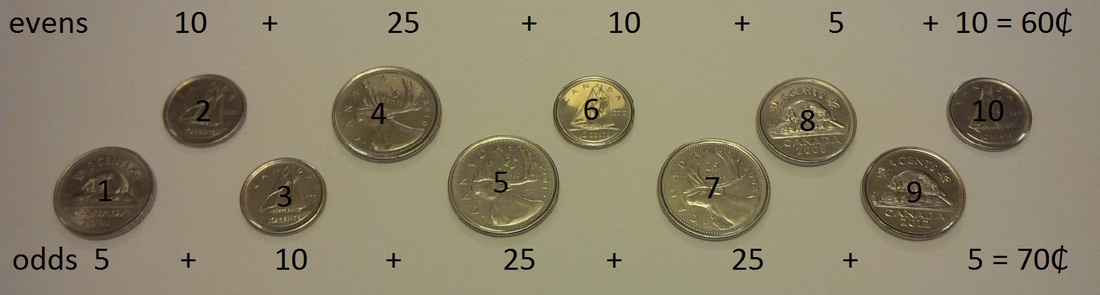

 RSS Feed
RSS Feed