|
I was recently looking for an activity to explore a linear relationship, preferable one that included some practice with decimals. I found a few examples but none of them really seemed to satisfy what I was looking for. Here are a few of my criteria for good experiments to explore function relationships:
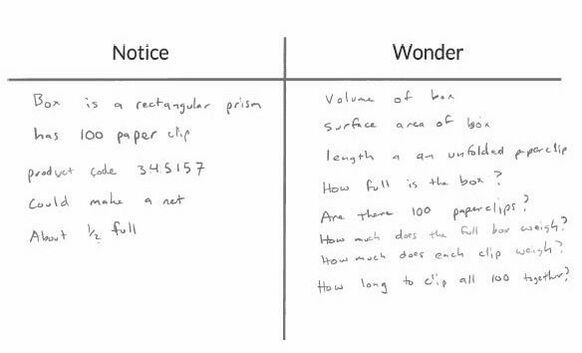
Notice and WonderThere were some great questions about volume and surface area, weight, and size of the paper clips (what is a #4 sized paper clip?). The questions the we went on to investigate was how long would it take to make a paper clip chain from all 100 paper clips. I was inspired by Dan Meyer's Guinness World Record for the longest paperclip chain in 24 hours. Dan blogged about breaking the record as well as asking student to see how many paperclips they could chain in one minute. EstimationI asked students to estimate how long they thought it would take to create a chain of 100 paper clips. I also asked them to think about an estimate that they know was too low (that creating a chain this fast was not possible) and too high (that they would have no problem creating a chain in this time even going slowly). Most students thought that a time between 5 and 6 minutes was a good "just right" estimate. Gathering Data
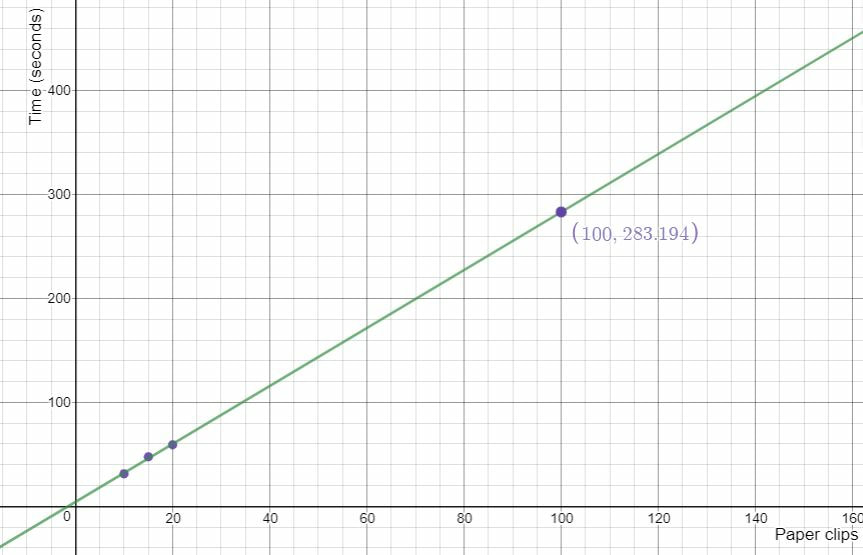
Revising EstimatesAfter collecting and analyzing some data, I ask students if they'd like to revise their estimate for 100 paper clips. Then we test their revised estimate using a plot of the values they collected and extrapolating. Below is one student's data plotted in Desmos. They estimated 300 seconds (5 minutes) to chain all 100 paperclips. This lesson could be modified to include outcomes from a number of different grade levels. I closed the lesson by showing students the record for the most paper clips linked together in one minute and asked students how they would compare. Nova Scotia Mathematics Curriculum Outcomes Mathematics 6 SP01 - Students will be expected to create, label, and interpret line graphs to draw conclusions. Mathematics 6 SP02 - Students will be expected to select, justify, and use appropriate methods of collecting data, including questionnaires, experiments, databases, and electronic media. Mathematics 6 SP03 - Students will be expected to graph collected data and analyze the graph to solve problems. Mathematics 7 PR02 - Students will be expected to create a table of values from a linear relation, graph the table of values, and analyze the graph to draw conclusions and solve problems. Mathematics 7 N02 - Students will be expected to demonstrate an understanding of the addition, subtraction, multiplication and division of decimals to solve problems (for more than one-digit divisors or more than two-digit multipliers, the use of technology is expected). Mathematics 7 SP01 - Students will be expected to demonstrate an understanding of central tendency and range by: determining the measures of central tendency (mean, median, mode) and range; determining the most appropriate measures of central tendency to report findings. Mathematics 7 SP02 - Students will be expected to determine the effect on the mean, median, and mode when an outlier is included in a data set. EL
The Sno Cap Drive In in Sisters, Oregon is a diner that serves homemade ice cream and old fashioned burgers. The food here is great and the homemade ice cream is delicious. I stopped in this summer for a scoop of Cookie Monster ice cream. While waiting in line, I had some time to notice and wonder about the prices listed on the menu. What is going on here? NoticingI noticed the differences in price between having your burger with potato chips or with french fries. Depending on the burger you're having, it costs anywhere from 45¢ to 95¢ more to have fries instead of chips. I also noticed the difference between the burgers with cheese and those without cheese. To add cheese to your deluxe burger is an additional 80¢ but to add cheese to your bacon burger is only an additional 30¢. WonderingIs there a pattern or rule to the price differences between having a burger with chips or fries? The list of differences between chips and fries is: 70¢, 70¢, 65¢, 60¢, 45¢, 80¢, 75¢, 75¢, 95¢, 70¢, 65¢, 70¢, 70¢, 65¢, 80¢, 60¢. The values range from a minimum of 45¢ to a maximum of 95¢. The mean difference is 70¢ and the standard deviation (a measure of variation) is 11¢. I tried sorting the burgers in a variety of ways but there appears to be no pattern to the difference in price between chips and fries. This restaurant is in Oregon, which has no sales tax (one of only five such states), so the prices are not set so that when tax is applied, the total is a round number. I'm assuming that every burger gets the same amount of fries, but perhaps this isn't the case. I wonder if they get many questions about this? If you wanted to give the prices on this menu an overhaul, how would you price these burgers, chips and fries? Could you come up with a more logical system of pricing? What factors would go into making these price decisions? Which burger do you think is currently the most profitable based on the current prices? Nova Scotia Mathematics Curriculum Outcomes Grade 7 SP01 - Students will be expected to demonstrate an understanding of central tendency and range by: determining the measures of central tendency (mean, median, mode) and range; determining the most appropriate measures of central tendency to report findings. Grade 7 N02 - Students will be expected to demonstrate an understanding of the addition, subtraction, multiplication and division of decimals to solve problems (for more than one-digit divisors or more than two-digit multipliers, the use of technology is expected). Mathematics 11 S01 - Demonstrate an understanding of normal distribution, including: standard deviation and z-scores. EL
Here are a few questions that I thought about:
Below are some additional photos: Given the list of lego bricks, you could ask students a number of additional questions:
The Discovery Centre is currently working on a project to build Canada's largest Lego mosaic wall. The wall will be installed at the Discovery Centre's new location when it moves. Nova Scotia Mathematics Curriculum Outcomes Mathematics 7 - N07 Students will be expected to compare, order, and position positive fractions, positive decimals (to thousandths), and whole numbers by using benchmarks, place value, and equivalent fractions and/or decimals. Mathematics 8 - N03 Students will be expected to demonstrate an understanding of and solve problems involving percents greater than or equal to 0%. Mathematics 8 - N04 Students will be expected to demonstrate an understanding of ratio and rate. Mathematics 9 - N03 Students will be expected to demonstrate an understanding of rational numbers by comparing and ordering rational numbers and solving problems that involve arithmetic operations on rational numbers. Mathematics at Work 11 - G02 Students will be expected to solve problems that involve scale. EL
Revisiting the Classic Ferris Wheel Problem
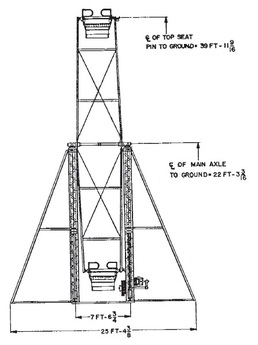
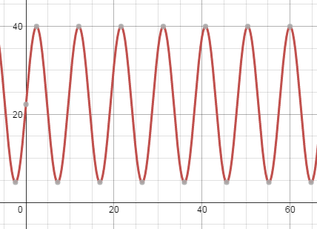
This type of pseudo-context word problem robs students of the opportunity to explore and analyze real-world problems in much depth. Dan Meyer has written quite quite a lot about pseudocontext. My concern with the Ferris wheel problem is not that you can't model the height of a seat on a Ferris wheel with a sine function, it is why would you do it? Instead of doing a textbook problem with a fictional Ferris wheel, I decided to use a real Ferris wheel from a nearby amusement park that some of my students would be familiar with. I visited the park to take a video of the Ferris wheel in action. Below is a 30 second clip of the "Big Ellie" Ferris Wheel at Atlantic Playland. Notice and WonderI started by asking students what they noticed in the video. After brainstorming and recording the students observations I asked students what they wondered about in the video. They asked questions like "how fast is the ride going?", "how tall is this Ferris wheel?", "how far can you see from the top of the ride?", "how long does the ride last?". In order to investigate these questions further we needed to estimate some values such as the radius of the wheel, how long it takes to make one revolution, and the height of the central axis about the ground. I asked students to estimate these values using the clues in the video we watched. We watched it several times in order to get some good estimates. I also talked about some of the mental math required to operate a ride like this. Because it is belt driven, you have to load the Ferris wheel so that it is equally balanced around the wheel. Otherwise, one side of the wheel would become too heavy and the drive cable would slip in the rim and the wheel wouldn't be able to turn! This requires a lot of on the fly estimates of weights of the riders as it is being loaded. In order to get a see how good we did with our estimations we turned to the internet in order to try to hunt down some of these values with a Google search. This lead to a discussion about what keywords we could use to hunt down this information. A search of "height of the central axis of the Ferris wheel at Atlantic Playland" was not very fruitful... an essential skill to solve a problem like this is to translate mathematical language into common terms that you can use for a Google search. Ve Anusic has a great blog post where he discusses a similar problem and the discussion with his students about the information you need and the information you might find online. First we did a search to find Atlantic Playland's website and found that they called their ride "Big Ellie". A search for this name lead us to believe that this Ferris wheel is a No. 5 Big Eli wheel made by Eli Bridge (I later emailed the park and confirmed that this is indeed the model of their Ferris wheel). Eli Bridge's website gave us some interesting information but not exactly what we were looking for. A bit more searching and we were able to find a pdf of the owner's manual for this ride that included a helpful diagram.
It is only after we were able to answer some of the students' questions regarding the video of the Ferris wheel did we start to talk how we might mathematically modeling the height of a person riding the wheel over time and the periodic nature of this function. Students were much better able to make sense of this visual model once they had a good grasp of the context of the problem.
Nova Scotia Mathematics Curriculum Outcomes Mathematics 12 - RF03 Represent data, using sinusoidal functions, to solve problems. Pre-calculus 12 - T04 Graph and analyze the trigonometric functions sine, cosine and tangent to solve problems. EL
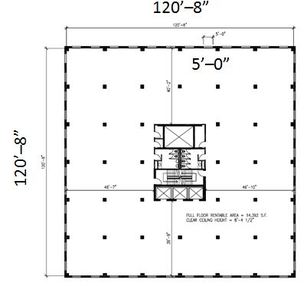
I drive past this building every day on my way to work. It is Young Tower at 6080 Young Street in Halifax. I think it is pretty interesting... I used this picture as a problem solving warm up activity for a group of grade 10 math teachers recently. I gave each group of teachers a large piece of chart paper and asked them to divide the paper in half with a line. I asked teachers to brainstorm what they notice about this picture and record it on one half of their chart paper. I asked them to look at the picture using a number of lenses. What would an architect notice about this image? What would a person who worked at this building notice about this picture? What would a mathematician notice about this picture? After about 5 minutes of brainstorming, I asked each group to tell me one thing they noticed and I recorded it at the front of the room. Groups noticed things like the number and size of windows on the building ("about half the lateral surface is glass"), the shape of the building ("almost a cube"), the picture must have been taken on a weekend because there are very few cars in the parking lot, and the weather was really nice that day. Next I asked them to brainstorm what they wonder about this picture and record in on the other half of their chart paper. If this picture was the start of a math problem, what could that math problem be? What things that they noticed sparked their curiosity? After another 5 minutes, I asked each group once again to tell me one thing that they wondered. After looking at all the questions that the groups posed, we selected one and asked everyone to estimate an answer to that question. I also asked them what information would they need to make a more accurate estimate. Once they had an initial estimate, I gave them some additional information about the building and let them revise their estimate. We had several really interesting questions posed by groups. Some questions concerned the shape of the building, like "How close to a perfect cube is this building?" Other questions focused on finance such as, "How much revenue is generated by leasing all of the office space in this building?" One of my favourite 'wonderings' was, "How much wrapping paper would it take to wrap this building up like a Christmas present?"
This "I Notice/I Wonder" problem solving strategy is one that I saw shared by Max Ray-Riek from the Math Forum. He has a blog where he talks about Noticing and Wondering in High School. This strategy starts off with brainstorming to let students get familiar and engaged with a problem situation before jumping into a specific question to solve. By having students come up with questions, you'll often get more engagement and interest. It also allows you to respond to interesting suggestions from students that you might not have considered. It allows everyone in the class meaningful participation in the conversation because everyone has something that they can notice. This strategy might also create additional opportunities for differentiation by using several different questions that students suggested. EL
|
Categories
All
|













 RSS Feed
RSS Feed