|
I recently did an activity with students to answer a question by collecting and analysing data. I was inspired by similar activities from Bruno Reddy, Mean Paper Aeroplanes, and Julie Reulbach, Paper Airplanes for Measures of Central Tendencies. We started class by watching a video of the Paper Airplane World Championship - Red Bull Paper Wings 2015. This short video (about 3 minutes) shows the highlights of three paper airplane competitions; Distance, Airtime, and Aerobatics. After watching the video I let students know that we would be making paper airplanes for a distance competition. Brainstorming
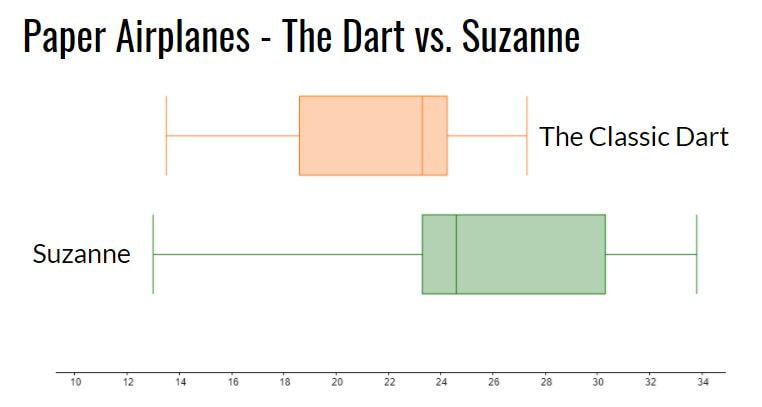
PredictionsNext I showed students two different paper airplane designs; the Suzanne and the Classic Dart. I asked students to predict which would fly the farthest. I also asked how much difference, if any, they expected to see between the two designs. Most students predicted that the Suzanne would fly farthest. The next step was to create an experiment in order to test our predictions. The ExperimentWe split the class in half. Each half followed a specific set of instructions to fold one or the other of these planes (I had a handout with instructions for each design). We used different coloured paper for each design. Each student threw their plane three times and recorded each flight distance. We measured in feet since the floor tiles in the hallway were one square foot. The students then calculated their mean distance and shared this mean with their team. Each team then calculated a five number summary and sketched a box plot for their data. The ResultsStudents declared the Suzanne to be the clear winner. The low ceiling height in the hallway seems to have favoured the glider design. We conjectured that the Dart may have performed better than Suzanne if they were thrown outdoors where students could throw at a higher launch angle. We also conjectured that the greater variation in the data for Suzanne was a result of the more complex folding required. Some planes were folded very well and others were a bit of a mess. Reflection
We finished class by watching a video of the world record throw for distance (we just watched the first 3 minutes of the video). The Suzanne, designed by John Collins and thrown by football quarterback Joe Ayoob holds the Guinness World Record for the farthest flight by a paper aircraft. The record throw was 226 feet, 10 inches (approx. 69.14 m). Our longest flight was just over 40 feet. Students seemed to really enjoy this activity. It allowed them to incorporate some movement in class and asked them to use mathematics and statistics in an authentic way to answer a real question. Update 26 April 2022 - Looks like there may be a new world record paper airplane throw. An attempt from April 16, 2022 went 77.134m! https://www.youtube.com/watch?v=7Mdgta-0dtE Nova Scotia Mathematics Curriculum Outcomes Extended Mathematics 11 S01 - Analyze, interpret, and draw conclusions from one-variable data using numerical and graphical summaries. Mathematics 9 SP03 - Students will be expected to develop and implement a project plan for the collection, display, and analysis of data by: formulating a question for investigation; choosing a data collection method that includes social considerations; selecting a population or a sample; collecting the data; displaying the collected data in an appropriate manner; drawing conclusions to answer the question. EL
I was recently asked by a junior high school to support their math teachers to infuse opportunities for movement into their math classes. I've been brainstorming some ideas and I thought I would share them here. I'm including some general routines for including movement in meaningful ways as well as some examples of activities for specific math outcomes. I'm not including generic "brain breaks" or "movement breaks" which are short burst of physical activity designed to energize students. Math Movement RoutinesStand and Talks from Sara VanDerWerf - Sara describes a tweak to the standard “Think/Pair/Share” routine that has greatly improved the number of students participating in her classroom discussions. This strategy incorporates movement that gives every student a chance to talk out loud and share their ideas without distractions. “Learners, I’d like everyone to stand up. Do not have anything in your hands. No calculators. No notebooks. No phones or pencils. Nothing. In a moment I am going to give you something that I want you to look at with a partner... I want to hear you asking each other things you wonder about. Please go now and find your partner.” Vertical Non-Permanent Surfaces (VNPS) from Peter Liljedahl - Students work in small groups standing at vertical non-permanent surfaces such as chalk boards or dry erase boards around the perimeter of the classroom. This allows the teacher to easily see what each group is working on and encourages discussion. The non-permanent nature of the surface lowers the risk of making mistakes and prompts students to start working faster and persevere longer. Check out posts from Alex Overwijk, Nathan Kraft and Laura Wheeler discussing this instructional strategy. Math "Scavenger Hunts" / Circuit Training / Around the World - The idea of a math scavenger hunt is that questions are posted on the walls around the room. The answer to each question will lead to the next question. Students move from question to question until they have completed the loop. The activity is self-checking because if students don't find their answer then they know they've made a mistake and need to work to correct it. I've blogged about this activity in the past and have used a number of variations of it. A teacher recently showed me a variation of called Math Stations Maze where the questions are numbered and the multiple choice answers lead to the next station similar to a choose your own adventure novel. Math Stations - This instructional strategy does not have to be complicated. I've seen teachers successfully push some desks together to make stations and put some math problems at each station. Students work in small groups completing the questions at their station and move to the next station when finished. I like to have one more station than there are groups so that there is always an open station to move to. This helps to minimize wait time between stations. It takes a bit more up front work, but I like to have an add-em up activity at each station so that students immediately know if they've answered the questions correctly. With this type of activity, the sum of the answers to several problem are given. If the students sum is not the same, they know that there is a mistake and work together to find where it is. Take Your Class Outside - Every once in a while, when the weather is nice, it is great to get outside. Stock up on some sidewalk chalk and hit the pavement to do some math. Not only do students get up and moving, they get some time to practice as well as decorate the playground or sidewalk with beautiful mathematics. Outcome Specific Examples from the NS CurriculumGrade 9 G02 Similar Polygons - You might measure the height of a flagpole or other tall object using a mirror and similar triangles. Here is a tweet showing photos of students engaged in this activity. Grade 9 PR07 Linear Relations - Barbie Bungee. Students determine a relationship between the number of rubber bands used in a bungee cord and how far a Barbie/action figure will fall. They this use this information to extrapolate how many rubber bands to use for an exciting bungee jump from a set height. Grade 8 PR01 Linear Graphing - Body Graphing/Algebra Walk. Set up a large Cartesian plane on the ground (outside with chalk or indoor with painters tape). Ask students to choose a spot on the x-axis, (and make sure that some choose negative numbers). Take a portable whiteboard with you (or you could write out some functions on paper in advance), and write a linear function (for example y = 2x + 3). Ask each student walk to their correct (x, y) coordinate given their starting x value. Here is a video from the Teaching Channel demonstrating a similar idea. There is also a description and video of this activity from Martin Joyce (@martinsean).
Grade 7 N01 Divisibility - Divisibility Hop. Stations are set up around the room, each with a 3 or 4 digit number. The teacher calls out a number. If students are standing at a station with a number that is divisible by the number the teacher called, they hope to a new station. Grade 7 G03 Transformations - Have students use the floor tiles as a coordinate plane then graphing various transformations with painters tape. Grade 7 N07 Fractions and Decimals - Put(t)ing Rational Numbers in Order. Teams of students work to put rational numbers and decimals in the correct order and then putt a golf ball in the style of the Price is Right television show Hole in One game. You could alter this game to put the rational numbers on cards and deal cards to each person on a team and then they have to stand in the correct order. Grade 7 PR07 Equations - Linear Equation Groups. Introduce this activity by calling out a small positive integer (for example 3). Students move about the room to form groups of that size. Once students are familiar with this activity, you can call out and/or write a linear equation on the board (for example 2x + 1 = 7). Students solve the equation and then move into new groups of that size. There are lots of different ways to incorporating movement into mathematics. Do you have additional suggestions of activities or resources for getting your junior high students moving around? Please consider sharing your ideas and I'll add them to this list. EL
|
Categories
All
|





 RSS Feed
RSS Feed