|
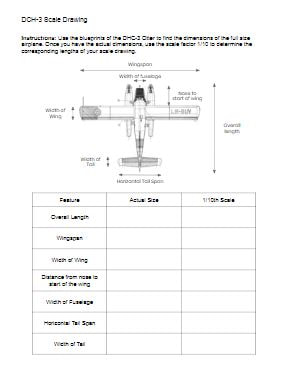
Students work with scale in a number of mathematics courses in Nova Scotia. In the Mathematics Essentials 12 course, they work with scale in conjunction with reading blueprints. This scale activity uses the blueprints for an iconic Canadian airplane, the DHC-3 Otter. I started the lesson with some estimation. I didn't let students know the name of the airplane to start with so that they don't just Google the name of the airplane and find out the actual length. Instead they use clues from the photo to make an estimate. Some references might include the size of the dock or ramp, the height of the wing, or the size of the windows or door. We use a routine I learned from Estimation180 to ask for an estimate they know is too low, an estimate they know is too high and then a just right estimate. After everyone had made and estimate, I showed them an image from a blueprint and asked them if they'd like to revise their estimate using some additional information. On the blueprint, they can see a scale drawn above the plane. Students use this information to either confirm or adjust their estimate. We can then use the scale to measure the image to find out the actual length of the plane (about 41 ft). After this opening activity, I showed them a picture of a 1/48 scale plastic model and ask them to tell me what the size of the finished model is knowing the size of the actual plane and the scale factor. The opening estimation allowed students a chance to think about scale. Next I handed out the blueprints for the plane. Our task was to use the blue prints to help create a 1/10th scale drawing of the top view of the plane using painters tape on the floor.
Students worked in small groups to recorded their measurements and calculate the measurements for the scale drawing. Once they were finished each group was provided with some painters tape and measuring tapes in order to make their scale drawing on the floor. It could be nice to have one group do their drawing on the wall, then it could stay up as a reference to their work with scale. We also talked about writing their measurements on the painters tape as they put it down. Variations and ExtensionsStudents who finish quickly can continue to add additional details such as the pontoons. This activity could also be done with larger groups creating a life size drawing of this plan using sidewalk chalk outside (weather permitting). NS Outcomes:
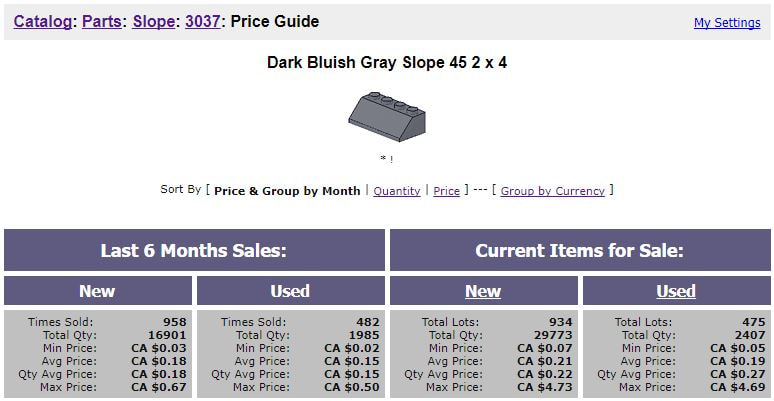
Mathematics Essentials 12 - 3.1 Calculate the dimensions of actual objects using blueprints with various scales Mathematics 11 - M02 Solve problems that involve scale diagrams, using proportional reasoning Mathematic at Work 11 - G02 Students will be expected to solve problems that involve scale; and G04 Students will be expected to draw and describe exploded views, component parts and scale diagrams of simple 3‑D objects. Mathematics Essentials 11 - E4 create 2-D scale diagrams and 3-D scale models Mathematics 9 - G03 Students will be expected to draw and interpret scale diagrams of 2-D shapes. Over the Christmas holiday, the number of LEGO bricks in my house increased significantly. My son received LEGO sets as gifts from numerous grandparents, aunts and uncles. I was a LEGO fan when I was a child and now I have an excuse to play with them again as an adult. We've had lots of fun recently building sets and designing our own creations. At some point I became inspired to create a scale model of our home. Planning and BuildingI started this small project by building a test model to try out the proportions and to see what kinds of bricks I would need. The sizes of the door and window established the overall size. I continued revising the structure it until it looked right and then started collecting the bricks I needed. Building this model reminded me of working on an OpenMiddle.com math problem. In an "open middle" problem, there is a one starting point and one solution but many different paths to get to the solution. With LEGO, there are many different ways to create, revise and improve your model. There are lots of different building techniques that will all result in a well designed scale model. ScaleAfter I created my initial rough model I did some reading up on LEGO scale. It turns out that it is a fairly complex topic that lots of different people have investigated. I found the Brick Architect web site to be very helpful. For "classic minifigure" scale a ratio of 1:42 can be used. One major difficulty in discussing scale is that the proportions of a LEGO minifigure are not even close to the proportions of an actual person. A LEGO minifigure is about 4 cm tall and 1.6 cm wide. An average male human is about 175 cm tall and 40 cm wide... about half as wide as a minifigure would be at that height. Another challenge is converting units. The architectural drawings of my house are in feet, which I converted to metric (cm), then a scale factor is applied and finally the metric units are converted into LEGO bricks. I found an awesome tool that does this all for you, the LEGO Unit Converter. FinanceI used a lot of estimation to determine how many bricks of each type I would need. LEGO bricks are not cheap so you don't want to order more than you need (Check out Jon Orr's activity involving cost, Is LEGO Gender Biased?). I purchased the bricks I needed on BrickLink.com, a large online LEGO marketplace. BrickLink provides a detailed price guide for every brick available which makes it really easy to know if you're getting a good deal or not. I needed lots of 45 degree angle slope bricks for the roof of my house. These price stats let me know what a reasonable price is to pay for new or used bricks of this type. It is amazing to see how many bricks are sold on this site. I think that the stats from this site could make for an interesting grade 12 math research project. The Finished Project
EL
Scale is a concept that is found at numerous grade levels in the Nova Scotia Mathematics curriculum. Scale drawings and models, similar polygons, and proportions are all found in mathematics outcomes. In math, scale is the ratio of the length in an image (or model) to the length of the actual object. Below is a question relating to scale factors. A scale factor is the ratio of any two corresponding lengths in two similar geometric figures. Take a look at the three different versions of Connect Four. Estimate the scale factor between each pair of game boards from the given pictures. Estimate the radius of each of the coloured chips. Is the scale factor of the radius of each coloured chip the same as the scale factor of their volume? You might ask students how scale is different from proportion. Try out this question: How big would a game board of Connect Four Hundred be (or even Connect Four Million) compared to Connect Four? In visual arts, scale refers to the size ratio between objects within an image. Using a consistent scale will make a drawing look more realistic. Objects do not appear too large or too small when compared to each other. Sometimes however, an artist might intentionally change the scale of certain objects in an image. One such technique is called 'Hieratic scale' or sometimes 'Hierarchical proportion'. This technique can be seen in paintings and sculpture from the middle ages where powerful or holy people were sometimes painted larger than ordinary or less important people to show their relative importance. The larger a person was, the greater their importance.
It would be fun to show students examples of how visual artists play with scale in order to make an impact on the viewer. Students might even be given an opportunity to create a piece of art that has an exaggerated or inconsistent scale or plays with forced perspective. Nova Scotia Mathematics Curriculum Outcomes Grade 6 N05 - Students will be expected to demonstrate an understanding of ratio, concretely, pictorially, and symbolically. Grade 8 N04 - Students will be expected to demonstrate an understanding of ratio and rate. Grade 8 N05 - Students will be expected to solve problems that involve rates, ratios, and proportional reasoning. Grade 9 G03 - Students will be expected to draw and interpret scale diagrams of 2-D shapes. Math at Work 10 G03 - Students will be expected to demonstrate an understanding of similarity of convex polygons, including regular and irregular polygons. Mathematics Essentials 11 D9 - calculate scale factors in 2-D scale diagrams and 3-D scale models understand the relationship among the scale factor and the related change in area or volume.Math at Work 11 G02 - Students will be expected to solve problems that involve scale. Mathematics 11 M03 - Demonstrate an understanding of the relationships among scale factors, areas, surface areas and volumes of similar 2-D shapes and 3-D objects. EL
Here are a few questions that I thought about:
Below are some additional photos: Given the list of lego bricks, you could ask students a number of additional questions:
The Discovery Centre is currently working on a project to build Canada's largest Lego mosaic wall. The wall will be installed at the Discovery Centre's new location when it moves. Nova Scotia Mathematics Curriculum Outcomes Mathematics 7 - N07 Students will be expected to compare, order, and position positive fractions, positive decimals (to thousandths), and whole numbers by using benchmarks, place value, and equivalent fractions and/or decimals. Mathematics 8 - N03 Students will be expected to demonstrate an understanding of and solve problems involving percents greater than or equal to 0%. Mathematics 8 - N04 Students will be expected to demonstrate an understanding of ratio and rate. Mathematics 9 - N03 Students will be expected to demonstrate an understanding of rational numbers by comparing and ordering rational numbers and solving problems that involve arithmetic operations on rational numbers. Mathematics at Work 11 - G02 Students will be expected to solve problems that involve scale. EL
|
Categories
All
|


















 RSS Feed
RSS Feed