|
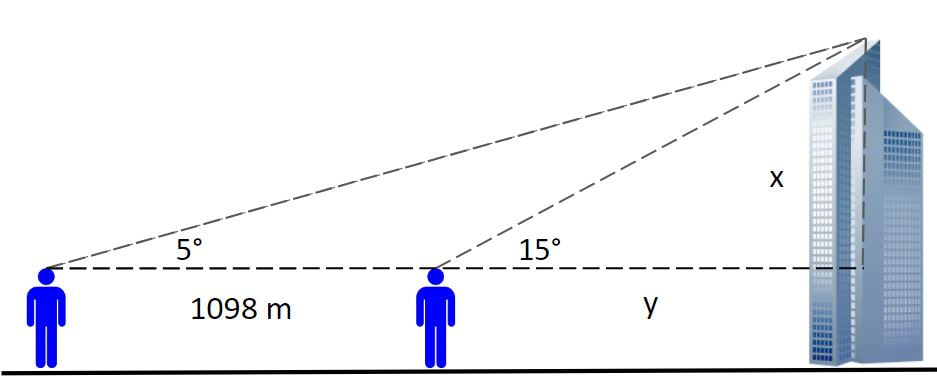
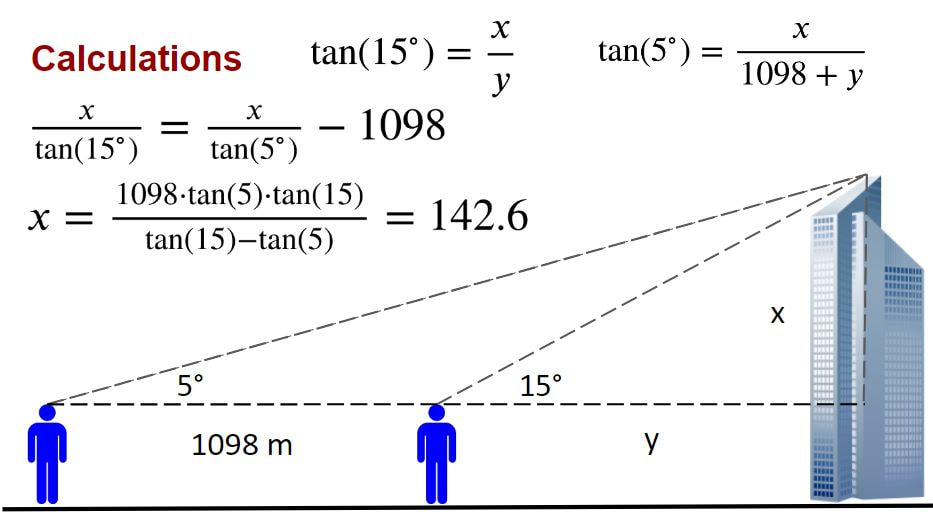
There is a new building going up in my neighborhood. It is so tall, that you can see it from the school I teach at. It makes me curious... how far do you think you could see from the top? As my students are learning about trigonometric ratios, I thought this might be an opportunity to bring the community into the classroom. I asked students to make a prediction about how far they could see given the pictures below. I also let them know that if you stand on the beach, you can see the horizon about 4.8 km away for an average height person (a lot of their initial guesses were even less than this). The first step in satisfiying my curiosity is to collect some data. On my bike ride home, I stopped a couple times to take a picture of the building and to use my Invicta MK1 clinometer to measure the angle of elevation to the top of the building. The first stop was just in front of the school and the clinometer measured about 5 degrees. About a kilometer further down the road, I stopped again for some more pictures and measurements. This time, the angle of elevation to the top of the building was about 15 degrees. I used Google Earth to measure a more precise distance between my two stops. It said that the places where I took the measurement were 1097.98 m apart... lets just call it 1098 m. Now to set up a picture of the situation and include some data. And now for some calculations... At this point, I paused to let the class know that I already knew the height of this building... and my answer was not nearly as accurate as I'd like it to be. I was able to find the building permit online and it says the the building is precisely 103327 cm tall... lets just say 103.3 m. So how did I get so far off? I asked my students to brainstorm some possible sources of error. One is my clinometer. I can only read the angle at an accuracy of about +/- 1 degree... and 1 degree of error at that distance makes quite a big difference in the height. Another source of error is the ground... unlike almost every textbook question, my city is not perfectly flat. Looking at a topological map, I can see that the ground rises about 20 meters over the distance that I took measurements. Not enough to look like you're on a hill but enough to make a difference in my calculations. One final source of error might be that my two measurements were not perfectly in line with the building. I'm not sure how much of a difference this might make but I know it added an additional bit of error. All in all, it was a good conversation about how real life is often not as simple as it looks in the textbook. So back to our question... how far can you see from the top? Well, that is where another right triangle can help. Given the height of the building (103.3 m), the location of the building on a hill (60 m above sea level) plus my height of eye (1.74 m), we can find out how far about sea level the viewpoint is. Since this building has a clear view of the ocean horizon, we can calculate the distance fairly accurately (I figured this part out after listening to an episode of the A Problem Squared podcast). So all these number and calculations tell me that, given the radius of the Earth (about 6371 km) and the height of the view (165.04 m) we have a view distance of 45.9 km. There was much rejoicing by the student who predicted the closest.
Can't Stop is a board game that was designed by Sid Sackson and released in 1980. It is a "press your luck" dice game in which players roll for dice and arranges them into two pairs. The sums of these pairs allow the player to progress their markers up the columns labeled with the values from 2 to 12. The goal of the game is to be the first to reach to top of three of these 11 columns. The height of the column is related to the probability that the sum will be rolled. The more likely the roll, the longer the column is. I was excited to find a copy of this game at a second hand shop recently. I've played Can't Stop online numerous times (at Board Game Arena) but this is a game where playing in-person seems better than virtual. The physical process of rolling and arranging the dice as well as interacting with other players makes for a better experience. I think it plays best with 2 or 3 players. They game is made for 2-4 players but I've seen people use the square plastic pieces from the game Advance to Boardwalk to add additional players in different colors. The Great Races
A nice user-created version of this paper and pencil game can be found at Board Game Geek. I like this version of the game because it is a quick game, with the "push-your-luck" aspect removed. Each player rolls just once, records their roll and then passes the dice to the next player. For a shorter game, you could play until 8 of the races are finished instead of completing all 11. Game at a GlanceBecause all the information about the game is contained on the game board, this is an excellent game for "Game at a Glance." Chad Williams has a collection of Game at a Glance images on his website, Beyond the Algorithm. Students are shown an image of a game in progress and could be asked a variety of questions.
I recently went camping and took this game along with me. I taught the game to several people (including kids) and because of the simple rules, they were all able to learn it in just minutes. Because all the pieces are plastic, they didn't blow away in the wind and if it got dirty, it could be easily rinsed off and cleaned. I think that this game would make a great addition to a mathematics classroom collection. What are your favourite games for the math classroom? Let me know! Nova Scotia Mathematics Curriculum Outcomes Mathematics 12 LR01 - Analyze puzzles and games that involve numerical and logical reasoning, using problem-solving strategies. Mathematics at Work 12 P01 - Students will be expected to analyze and interpret problems that involve probability. Mathematics at Work 11 N01 - Students will be expected to analyze puzzles and games that involve numerical reasoning, using problem-solving strategies. Mathematics Essentials 10 G4 - Compare predicted and experimental results for familiar situations involving chance, using technology to extend the number of experimental trials. Mathematics 8 SP02 - Students will be expected to solve problems involving the probability of independent events. Mathematics 7 SP06 - Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. EL
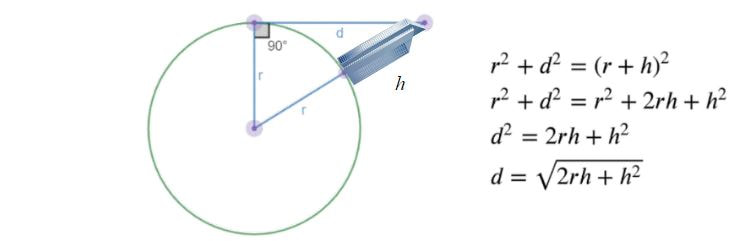
Where in your city or region can you see the farthest? The higher up you are, either in a building or on top of a hill (or a building on a hill), the farther you will be able to see. If there are no obstructions, you can see all the way to the horizon. With the Pythagorean Theorem and the radius of the Earth (r = 6,371 km), a few calculations can reveal the distance to the horizon (d) for any height (h). Given the height of my eye above the floor, 174 cm, if I stand on the beach and look out over the ocean to the horizon, I should be able to see about 4.708 km. A recent podcast from "A Problem Squared" (episode 022) featured a similar question. The question that was submitted by a listener asked, "What's the furthest away you can see something from earth, that is also on the earth?" This question made me think about a new building being built near where I live in Halifax. Richmond Yards, at a height of 103.3 m, it will be the tallest in Atlantic Canada when it is completed. It is also built one of the highest parts of the Halifax Peninsula at 60 metres above sea level. I wonder if the view from the top of this new building will be the longest view in Halifax? Or could it even be the longest line of sight in the province of Nova Scotia? So if I stand at the top of the Richmond Yards tower (103.3 m), located on a hill that is 60 m above sea level, how far should I be able to see if there are no obstructions? Using the formula above, my new height would be 103.3 m + 60 m + 1.74 m = 165.04 m. Given that height, the distance to the horizon would be 45.858 km. That is quite an improvement. Do you think there is a spot in your town or region where you could see farther? Where in Nova Scotia can you look the furthest away at something else, that is also in Nova Scotia? Do you know where the highest point in Nova Scotia is? What about in furthest view in all of Canada? From the top of the CN Tower? From the top of Mount Logan, the tallest mountain in Canada with a summit of 5,959 m? What other factors effect how far you can see? What about seeing past the horizon to a tall building or mountain that sticks up over the other side of the horizon? NS Outcomes: Mathematics 8 - M01 Students will be expected to develop and apply the Pythagorean theorem to solve problems. Mathematics 9 - M01 Students will be expected to solve problems and justify the solution strategy, using the following circle properties: [...] A tangent to a circle is perpendicular to the radius at the point of tangency. EL
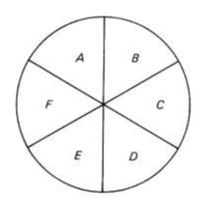
Brian Bolt has written numerous resource books for teachers containing collections of rich mathematical problems, puzzles, investigations and games. Some are descriptions of classic problems and puzzles while others are new creations. I think these books are a great resource and I wanted to share three of my favourite problems from them. Number the Sectors
This is problem #53 from Even More Mathematical Activities (1987) and problem #72 from The Mathematical Funfair (1989). Instead of starting by asking students to find a set of numbers that gives all the integers from 1 to 25, I like to create an example as a class and then challenge them to do better (get to a larger number). You can also ask them to prove what the maximum value is. Bolt has an alternate version of this puzzle in A Mathematical Pandora's Box (1993) (#12 Can you Do Better), which has 5 sectors around a central circle. This version can be found online at NRICH Maths as the Number Daisy. How Large a Number Can You Make?Make the largest number with just the digits 1, 2, and 3 once only once and any mathematical symbols you are aware of, but no symbol is to be used more than once. The challenge is to see who can make the largest number. Here are some numbers to get the ball rolling: This is problem #83 from Even More Mathematical Activities, (1987). I've given this as a warm-up problem for high school students and this often leads to a discussion of how to know which is bigger, 2^(31) or 3^(21)? Make a CenturyPut arithmetical signs in suitable places between the digits to make the following sum correct: 1 2 3 4 5 6 7 8 9 = 100 There is more than one solution. See how many you can find. This is problem #127 from Mathematical Activities (1982). I would start this challenge with students by asking them to make an expression using the numbers from 1 to 9 to make a value as close as possible to 100. I would then add on the challenge to try to find an expression exactly equal to 100. There is a very similar problem called Make 100 on NRICH Maths. I saw an earlier version of this as problem #94 in Amusements in Mathematics (1917) by Henry Ernest Dudeney. In Dudeney's version, he includes an additional challenge to try to find a solution which "employs (1) the fewest possible signs, and (2) the fewest possible separate strokes or dots of the pen. That is, it is necessary to use as few signs as possible, and those signs should be of the simplest form. The signs of addition and multiplication (+ and ×) will thus count as two strokes, the sign of subtraction (-) as one stroke, the sign of division (÷) as three, and so on." What are Your Favourite Problems?Do you have a favourite problem or puzzle from one of Brian Bolt's puzzle books? Do you have other favourite collections of puzzles? EL
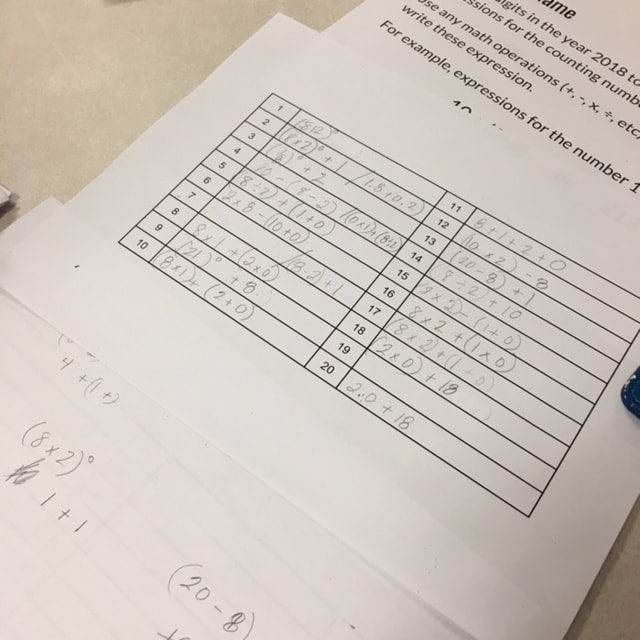
During a professional development session today with grade primary to grade 9 math coaches and support teachers, we spent some time working on solving some math puzzles. We used our work on these puzzles to reflect on what good group work looks and sounds like. We also discussed the characteristics of effective mathematical communication. It was great to see positive energy and teachers supporting and encouraging each other. Below are the five math puzzles and investigations that we worked on. We selected these puzzles because they are easy to explain, open to a wide range of students, and offered a fun challenge. 1-10 Card InvestigationThis problem from Marilyn Burns asks you to find a special order for a stack of cards, Ace through 10. Place the stack of cards face down and turn over the first card. It should be the Ace. Place the next card on the bottom of the deck and then reveal the top card. It should be the number 2. Continue placing the next card on the bottom of the deck and then revealing the top card until all the cards are revealed. The face up cards should now be in order from Ace to 10. Marilyn recorded a video to demonstrate these rules that is much easier to understand than my written instructions. Marilyn's has a description of this problem on the MathSolutions website. This logic problem doesn't rely on any prerequisite mathematical knowledge and you can try it out quickly to see if you've come up with the correct solution. It gives students a chance to work together to try out strategies. The Square-Sum ProblemCan you order all the numbers from 1 through 15 so that the sum of any two consecutive numbers are always a square number? For example, in the sequence: 4, 5, 11; 4+5=9 and 5+11=16.I really like this problem because there are some great extensions to take this problem farther and there is a very nice way to visualize the possible solutions. Numberphile has recorded a great video demonstrating both the problem and solution. The Year Game - 2018Use the digits in the year 2018 to write mathematical expressions for the counting numbers 1 through 100 (we only went to 20). Use any math operations (+, -, x, ÷, etc) and parentheses to write these expression. There is a more detailed description of this problem at the Math Forum website. For example, expressions for the number 1 might be: 10 ÷ (2+8) or 218^0. This problem is very similar to the classic Four Fours problem but with new digits each year. Which numbers are the hardest to find an expression for? Why do you think this is? I think this problem also leads nicely to a discussion about mathematical elegance and beauty. Look at a variety of expressions with the same value. Which expression do you think is the best? What makes for an "elegant" solution? Perimeter 12This problem challenged groups to make as many different shapes as possible with a perimeter of 12 units using a geoboard (or dot paper). Shapes were recorded on dot paper to make sure no shapes were repeated as reflections or rotations. I've seen variations of this problem in several places. One of them is Brian Bolt's book Mathematical Activities (1982). He suggests not only to find shapes with a perimeter of 12 but to also find the area of each shape. You can then find which shape has the maximum/minimum area. He also challenges students to find non-rectangular shapes (e.g. triangles) with a perimeter of 12 units. There were some good discussions about the lengths of diagonal line segments on the geoboard. Eight DominoesThis problem is from NRICH. Finding a solution took some perseverance but most groups were eventually successful. The problem challenges you to create a square using 8 specific dominoes (0-1, 0-2, 0-3, 0-6, 1-2, 1-4, 2-2, and 3-5). In the 4 x 4 square, each of the columns and rows should sum to 8. The 3-5 domino seemed to be key as the rest of the squares in that row (or column) had to be blank. What are your favourite math or logic puzzles? EL
I recently had the pleasure of attending the Nation Council of Teachers of Mathematics (NCTM) Annual Meeting and Exhibition in Washington, DC. This was my first big math conference. I attended some great presentations. One message that I heard reiterated in a number of presentations and one that resonated with me was about rich tasks. The message was that having a rich task is only a starting point for effective mathematics instruction. A rich task in math class is like being dealt a great hand of cards in Poker. It makes winning easier but it still takes a seasoned player with solid understanding of the complexities of the game to win a big pot. Full Stack LessonsDan Meyer presented a session called "Why Good Activities Go Bad" in which he discussed a math task called Barbie Bungee. After giving summary of the task he interviewed three different teachers on their use of the task and their students' experiences. Dan asked us to think about what makes a task engaging and productive and what might make it fall flat. He talked about "full stack" lessons and how the mathematical task itself is just one component of a fully developed and presented lesson. Engaging StudentsSara VanDerWerf, in her presentation ‘Engaging Students in Seeing Structure’, talked about her overarching goals when lesson planning. Using routines such as Notice and Wonder and Stand and Talks, Sara supports her students to see and talk about math concepts before they are formalized. Students have a chance to engage in the mathematics and build conceptual understanding. These types of routines which allow students to be curious about math and ask questions are important elements for getting the most out of a rich math task. Super (Secret) Mathematics of Game ShowsOne of the most engaging sessions that I went to at NCTM was presented by Bowen Kerins. He had a fun presentation called Super (Secret) Mathematics of Game Shows. A few elements of his presentation that stand out:
Rich ConversationsShortly after returning from NCTM, I saw these tweets above from Fawn Nguyen and from Cathy Marks Krpan. These thoughts sound like they reflect many of the messages that I heard in Washington, DC this year. This morning, I also saw John Rowe's blog post "The Secret Sauce of Great Lessons." It looks like he attended several of the same sessions that I did and had a similar reflection. My Lesson Planning ChallengeOne the first slide of my presentations, down in the notes, I often write, "The essential components of a presentation: a clear focal point, a strong flow and structure, a beautiful design and a compelling delivery." (I picked this quote up here). It serves as a reminder to stay focused and think about the structure of my presentation (or blog post for that matter). I need to create a similar reminder for planning lessons to focus on more than the task itself. I need to consider how that task will be implemented to make it as engaging and productive for students as possible. EL
Mathematics can be a nuanced subject. Subtle differences in the context or wording of a problem can lead to drastic differences in complexity. I find this especially true with the topic of combinatorics. I remember the first time I taught a course including counting with combinations and permutations. I created a worksheet for my students with what I thought were some fairly straight forward questions. It turns out that some of the problems I created were much more complicated to solve correctly than I had intended. I learned from this mistake and was much more careful from then on. My son and I were recently playing with a roll of tickets (a great math manipulative as it turns out). This led to some questions that appeared similar but were quite different in complexity. I took the pictures below and posted them to twitter. Sharing CandyThe answer to the question on the right can be calculated with a single combination. You can use the "stars and bars" approach to think about the calculation required. First you have to decide if everyone gets a candy or not. If everyone gets at least one candy, then you can think of the problem as putting the twelve candies in a row (the "stars") and inserting 3 dividers in between them (the "bars") to divide the row into four sections. As an example, {★★★|★★|★★★|★★★★} would be one solution. Mathematically, there are 12 identical objects placed in 4 distinct bins, such that all bins contain at least one object. Given the 11 spaces between candies, how many ways are there to choose three of these spaces to place dividers. For the same situation, if you allow each person to receive zero candies, there are more possibilities. Using the same "stars and bars" approach, you can think of all twelve candies and the three dividers and being placed in a row. How many ways are there to do this? There are a total of 12+3 spaces and either a candy or divider is placed into each one. As an example, {★★||★★★★★★|★★★★} would be one solution. Ripping TicketsThe answer to the question on the left regarding tearing tickets is actually a much more complicated question than the one on the right despite appearing very similar. In this question, we are separating identical objects into identical bins. This means that {★★|★★|★★|★★★★★★} is the same solution as {★★|★★★★★★|★★|★★} since they are both three groups of 2 and one group of 6. This type of problem involves partition numbers and they have been studied by mathematicians such as Leonhard Euler, Srinivasa Ramanujan and more recently Ken Ono. Partition numbers are an open area of mathematics research. The solution for this problem is closely related to partition numbers. For every natural number n, its partition number, p(n), is defined as the number of ways we can write it as a sum of positive integers. For example, since the number 3 can be written as three different unique sums (1+1+1, 1+2 or 3), we say that p(3)=3. If we were looking for the total number of ways to partition the twelve tickets into any number of groups, our answer would be p(12) = 77 (from OEIS A000041). In our problem above however, we're looking for the number of ways to partition 12 into exactly 4 positive integers. We can do this either by counting with an organized list (brute force) or using recursion. For a description of the recursion method, see https://brilliant.org/wiki/identical-objects-into-identical-bins/.
Exploring Problem StructuresI recently tried out some problem sets from Craig Barton's SSDD problem website. SSDD stands for Same Surface, Different Deep Structure math problems. These are a set of problems (typically four) that have a very similar context but different solution strategies. The intent is for students to focus on determining the structure of each question and then to identify the corresponding strategy needed to solve it. I think this is an interesting routine for mathematics outcomes where there are a large variety of similar structures (like solving quadratics word problems or combinatorics problems). Michael Pershan wrote a blog post reflecting on the SSDD problem structure and how it might cause students to think in different ways. This type of reflection is why I write this blog and read other teachers blogs. Michael continued the conversation on Twitter and suggested that SSDD problems, “vary the deep differences while keeping the surface the same, and you draw attention to the way minor differences trigger different structure” I think that the type of Same and Different question prompt that I wrote about above also generates the same type of student thinking about the solution strategies required to solve a problem. I think that the SSDD structure could lead to a variety of similar question routines. For example, you could give students variety of questions but instead of answering them, they could be asked to group the questions together that share a similar solution strategy. Or perhaps, you could give students a general context and ask them to create several different questions from this context connected to a variety of mathematics topics (similar to a Notice and Wonder strategy). I think it is exciting to have so much collaboration and thoughtful conversation online between mathematics educators. Nova Scotia Mathematics Curriculum Outcomes Mathematics 12 P05 - Solve problems that involve permutations. Mathematics 12 P06 - Solve problems that involve combinations. EL
An engaging puzzle with simple instructions is to ask students to create a rectangle using pentomino pieces. Let them figure out what rectangle dimensions are possible given the total number of squares in the pentominoes they're using (for a full set of 12 pentominoes, 3x20, 4x15, 5x12 and 6x10 are possible). You can also print off a variety of other shapes and challenge students to fill those shapes with pentominoes or have students create their own shapes and challenge their friends to solve them. Younger students can be challenged to fill an empty picture frame or tray with pentominoes. Here are five great games, puzzles and activities (in no particular order) that use pentominoes:
2. Pentomino Puzzles from Jon Orr (@MrOrr_geek) - Jon describes an activity where students are given a hundreds chart and a transparent pentomino. Ask students to place their pentomino on the hundreds chart so that it covers a sum of 135. Then ask students to share their strategies for finding the correct placement. Are there sums that are not possible to achieve? Continue the activity by selecting different tiles, giving different sums to find, creating equations and solving them. I also saw these questions posted by Amie Albrecht (@nomad_penguin) on twitter, "Can you find a pentomino that covers numbers that: sum to 150, sum to an even number, covers three multiples of 4, and more". Jon created an online Desmos Activity that allows you to do this activity virtually. 3. Pentomino Farms - I was introduced the the pentomino farms activity from Martin Gardener's book Knotted Doughnuts and Other Mathematical Entertainments. The task is to use the 12 pentominoes to build a fence around a field on your farm. The rule used to join the pentominoes to form a fence is that they must touch along the full edge of a square and not just at the corners. There are four types of farms to create. For each type, what's the largest field you can enclose?
4. How Convex is a Pentomino? - Which pentomino shape is the most convex? How do you measure "convexity"? This is an interesting question that generated lots of discussion on Twitter. Some interesting methods of measuring this were discussed by Alexandre Muñiz (@two_star) in his blog post, "Vexed by Convexity." I think it would make a great discussion for students to rank the pentominoes by convexity and then defend their choices.
If you have a favourite activity, puzzle or game featuring pentominoes, I would love to hear about it! EL
I prepared a lesson plan to work with a student. I carefully considered how I would introduce the topic, the path that the lesson might take and the questions that I would ask to prompt our discussion. I thought about the manipulatives that we might use to visualize and physically interact with the problem. I had a course carefully laid out. I started by drawing an irregular, kidney shaped area on the desk and asked the student how he would estimate the area of the shape. I was prepared for a number of different responses that I thought I might hear... but the student didn't follow my carefully plotted course for our lesson. Instead he replied, "I'd use Pick's Theorem." I grew up sailing on the Columbia River. When changing course on a sailboat, you can either turn the bow (the front of the boat) through the wind (i.e. tacking) or you can turn the stern (the back of the boat) through the wind (i.e. jibing). When tacking, the boom gently moves from from one side of the boat to the other. Jibing on the other hand can be dangerous as the boom suddenly jumps to the other side of the boat. When the student suggested Pick's Theorem, it felt like changing course by jibing instead of by tacking.
After our excursion through Pick's Theorem we found our way back to estimating the area with some manipulatives. First we covered the shape with square tiles and then we covered the shape with pennies. We found that we could cover the shape with 66 square tiles. I asked the student how the area we found with Pick's Theorem and the area we found with square tiles compared. Through our discussion we decided that we needed a common way to talk about these areas so we converted both to square centimeters. We found that the area from Pick's Theorem was 382.5 cm^2 and the area using square tiles was 412.5 cm^2. Next, we looked at our penny solution. We looked up the diameter of a penny online and found that 135 pennies at 2.85 cm^2 each gave us a total area of 384.75 cm^2. While discussing how this estimate compared to our others, the student started talking about Alex Thue and his theorem on circle packing (this student has a really good memory). The student remembered that the efficiency of hexagonal packed pennies was about 91%. So we used this efficiency to correct our penny estimate to make it even better. This led to another discussion that I hadn't planned on about tesselations and polygons that tile the plane. The student said he had read in a book that there were 14 irregular pentagons that tile the plane. His book was a few years old however so he didn't know that a 15th pentagon had been discovered in 2015 or other recent work in this area. While the lesson didn't go quite as I had planned, I was really happy to be able to take the student's contributions to the discussion and weave them into the overall narrative of our work. Being flexible, listening to students and incorporating their contributions into a discussion can sometimes throw you off course and you might end up someplace unexpected. The journey along these altered courses however can be incredible. EL
The Riddle of the Tiled Hearth is one of many mathematical puzzles from Henry Ernest Dudeney's 1907 book titled The Canterbury Puzzles And Other Curious Problems. The first group of puzzles in this book are based on the characters from Geoffrey Chaucer's Canterbury Tales. Puzzles from this book could be used as part of a cross curricular unit on history, literature and mathematics. There are a number of very interesting puzzles and games including the first pentomino puzzle called The Broken Chessboard and a clever variation of the game Nim called The Thirty One Game. Since this book was first published in 1907, the copyright has expired and it is freely available on Project Gutenberg. It seems that it was Friar Andrew who first managed to "rede the riddle of the Tiled Hearth." Yet it was a simple enough little puzzle. The square hearth, where they burnt their Yule logs and round which they had such merry carousings, was floored with sixteen large ornamental tiles. When these became cracked and burnt with the heat of the great fire, it was decided to put down new tiles, which had to be selected from four different patterns (the Cross, the Fleur-de-lys, the Lion, and the Star); but plain tiles were also available. The Abbot proposed that they should be laid as shown in our sketch, without any plain tiles at all; but Brother Richard broke in,-- To use this activity with students, I would start by introducing using the tiled hearth story as written above. Then I would introduce some manipulatives that would let them physically explore and work with the puzzle. I would give each group of students a large 4x4 grid on a sheet of paper and some multi-link cubes of 4 different colours.
One aspect of this puzzle that I like is that students can play around with it and have some intermediate success. They might just place a few cubes on the grid. With time, they can refine their solutions to get better and better. Below shows how a student might explore to place more and more cubes. The Solution from Canterbury Puzzles shows that the best solution leaves 3 blank spaces. Dudeney states, "The correct answer is shown in the illustration on page 196. No tile is in line (either horizontally, vertically, or diagonally) with another tile of the same design, and only three plain tiles are used. If after placing the four lions you fall into the error of placing four other tiles of another pattern, instead of only three, you will be left with four places that must be occupied by plain tiles. The secret consists in placing four of one kind and only three of each of the others." Below are both my solution using cubes and Dudeney's equivalent solution. EL
|
Categories
All
|










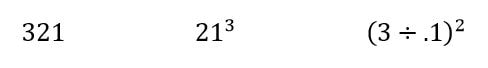

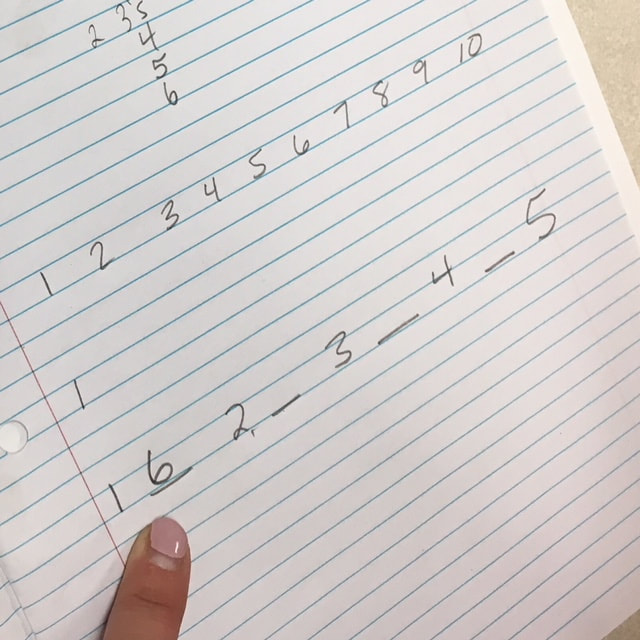


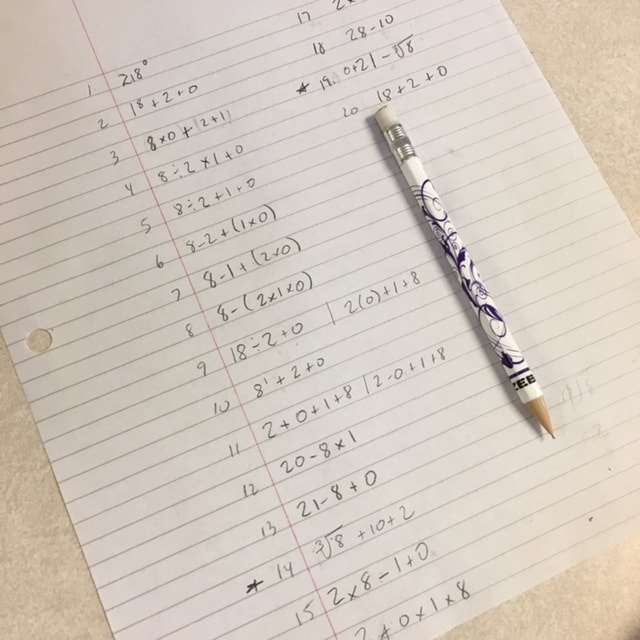










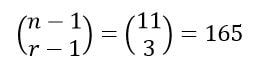
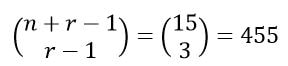






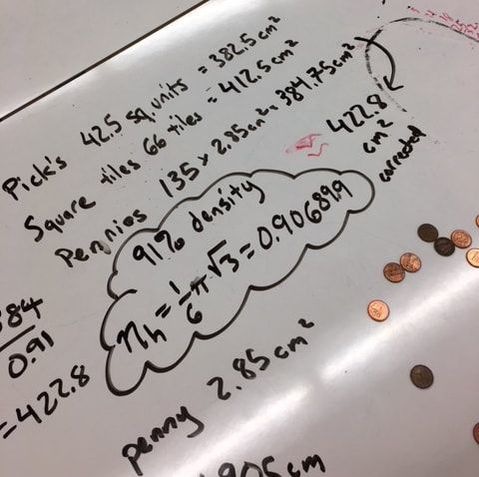







 RSS Feed
RSS Feed