|
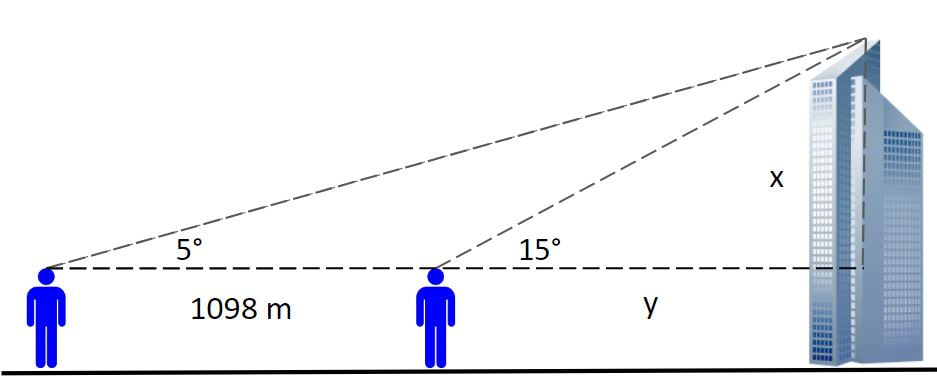
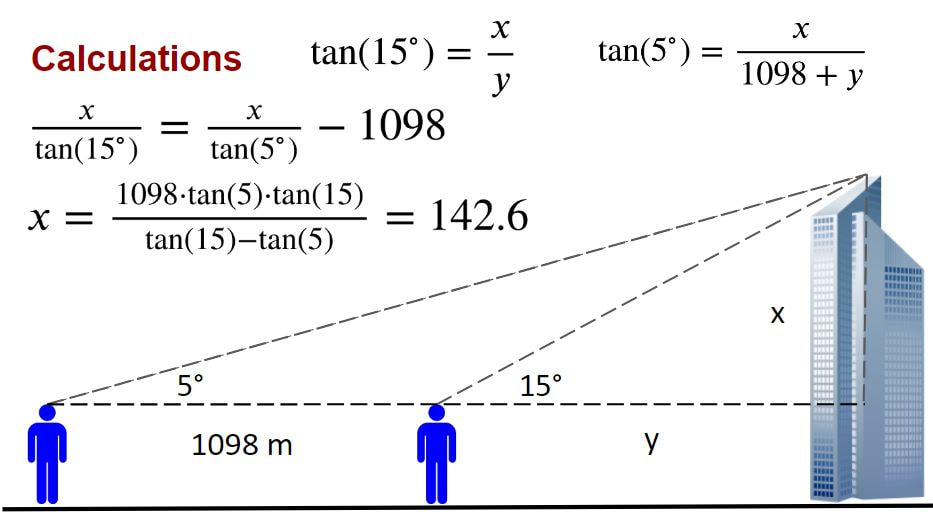
There is a new building going up in my neighborhood. It is so tall, that you can see it from the school I teach at. It makes me curious... how far do you think you could see from the top? As my students are learning about trigonometric ratios, I thought this might be an opportunity to bring the community into the classroom. I asked students to make a prediction about how far they could see given the pictures below. I also let them know that if you stand on the beach, you can see the horizon about 4.8 km away for an average height person (a lot of their initial guesses were even less than this). The first step in satisfiying my curiosity is to collect some data. On my bike ride home, I stopped a couple times to take a picture of the building and to use my Invicta MK1 clinometer to measure the angle of elevation to the top of the building. The first stop was just in front of the school and the clinometer measured about 5 degrees. About a kilometer further down the road, I stopped again for some more pictures and measurements. This time, the angle of elevation to the top of the building was about 15 degrees. I used Google Earth to measure a more precise distance between my two stops. It said that the places where I took the measurement were 1097.98 m apart... lets just call it 1098 m. Now to set up a picture of the situation and include some data. And now for some calculations... At this point, I paused to let the class know that I already knew the height of this building... and my answer was not nearly as accurate as I'd like it to be. I was able to find the building permit online and it says the the building is precisely 103327 cm tall... lets just say 103.3 m. So how did I get so far off? I asked my students to brainstorm some possible sources of error. One is my clinometer. I can only read the angle at an accuracy of about +/- 1 degree... and 1 degree of error at that distance makes quite a big difference in the height. Another source of error is the ground... unlike almost every textbook question, my city is not perfectly flat. Looking at a topological map, I can see that the ground rises about 20 meters over the distance that I took measurements. Not enough to look like you're on a hill but enough to make a difference in my calculations. One final source of error might be that my two measurements were not perfectly in line with the building. I'm not sure how much of a difference this might make but I know it added an additional bit of error. All in all, it was a good conversation about how real life is often not as simple as it looks in the textbook. So back to our question... how far can you see from the top? Well, that is where another right triangle can help. Given the height of the building (103.3 m), the location of the building on a hill (60 m above sea level) plus my height of eye (1.74 m), we can find out how far about sea level the viewpoint is. Since this building has a clear view of the ocean horizon, we can calculate the distance fairly accurately (I figured this part out after listening to an episode of the A Problem Squared podcast). So all these number and calculations tell me that, given the radius of the Earth (about 6371 km) and the height of the view (165.04 m) we have a view distance of 45.9 km. There was much rejoicing by the student who predicted the closest.
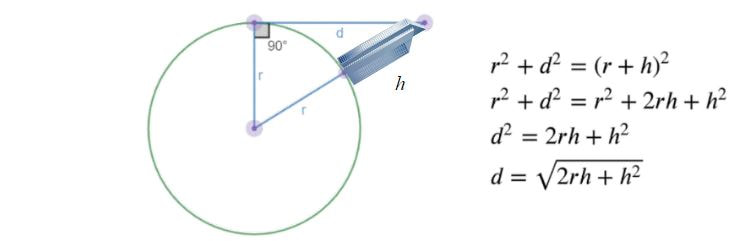
Where in your city or region can you see the farthest? The higher up you are, either in a building or on top of a hill (or a building on a hill), the farther you will be able to see. If there are no obstructions, you can see all the way to the horizon. With the Pythagorean Theorem and the radius of the Earth (r = 6,371 km), a few calculations can reveal the distance to the horizon (d) for any height (h). Given the height of my eye above the floor, 174 cm, if I stand on the beach and look out over the ocean to the horizon, I should be able to see about 4.708 km. A recent podcast from "A Problem Squared" (episode 022) featured a similar question. The question that was submitted by a listener asked, "What's the furthest away you can see something from earth, that is also on the earth?" This question made me think about a new building being built near where I live in Halifax. Richmond Yards, at a height of 103.3 m, it will be the tallest in Atlantic Canada when it is completed. It is also built one of the highest parts of the Halifax Peninsula at 60 metres above sea level. I wonder if the view from the top of this new building will be the longest view in Halifax? Or could it even be the longest line of sight in the province of Nova Scotia? So if I stand at the top of the Richmond Yards tower (103.3 m), located on a hill that is 60 m above sea level, how far should I be able to see if there are no obstructions? Using the formula above, my new height would be 103.3 m + 60 m + 1.74 m = 165.04 m. Given that height, the distance to the horizon would be 45.858 km. That is quite an improvement. Do you think there is a spot in your town or region where you could see farther? Where in Nova Scotia can you look the furthest away at something else, that is also in Nova Scotia? Do you know where the highest point in Nova Scotia is? What about in furthest view in all of Canada? From the top of the CN Tower? From the top of Mount Logan, the tallest mountain in Canada with a summit of 5,959 m? What other factors effect how far you can see? What about seeing past the horizon to a tall building or mountain that sticks up over the other side of the horizon? NS Outcomes: Mathematics 8 - M01 Students will be expected to develop and apply the Pythagorean theorem to solve problems. Mathematics 9 - M01 Students will be expected to solve problems and justify the solution strategy, using the following circle properties: [...] A tangent to a circle is perpendicular to the radius at the point of tangency. EL
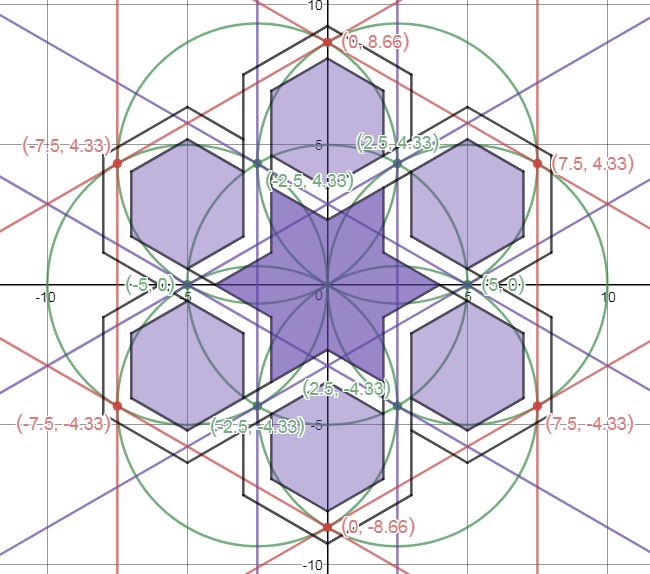
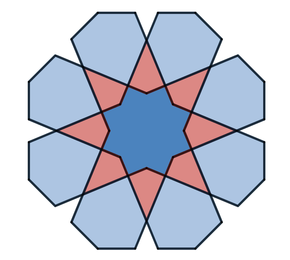
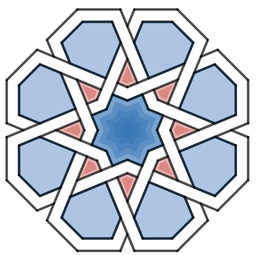
About a year ago, I signed up for Samira Mian's Udemy course on Islamic Geometry. I also purchased a copy of Eric Broug's book Islamic Geometric Patterns. I wanted to learn the basics so that I could determine if this might be a good way to satisfy the grade 7 mathematics geometric constructions outcome. I designed a short unit that I described last year. Recently, I decided to try replicating some of these patterns using the online Desmos calculator and geometry tool. I think having some experience drawing these patterns with a compass and straight edge was helpful. If you're looking for some Islamic geometric patterns to try, YouTube is a great place to get some ideas. There are some great instructional videos from Samira Mian and Nora Youssef, among others. The first pattern that I tried was a Star and Hexagon pattern that I learned from Samira's Udemy course. I learned that sticking with exact values are worth the effort. Rounding intersection points and slopes of lines to the nearest tenths or hundredths place work well at first but the errors compound and things start to get messy down the road. Interlacing the pattern gave me lots of practice with domain and range restrictions. 8 Fold RosetteNora Youssef has a nice video tutorial on for drawing an 8-Fold Rosette pattern. I did this pattern twice. The first time I constructed the basic pattern and the second time I added interlacing. I used the polygon function to add colour and figured out how to use trigonometry to rotate the polygons around the origin. This made it really efficient. I created a table with the vertices of the polygon and then just duplicated and rotated that polygon around the rosette. I duplicated the polygons multiple times to make the colours bold. Links:
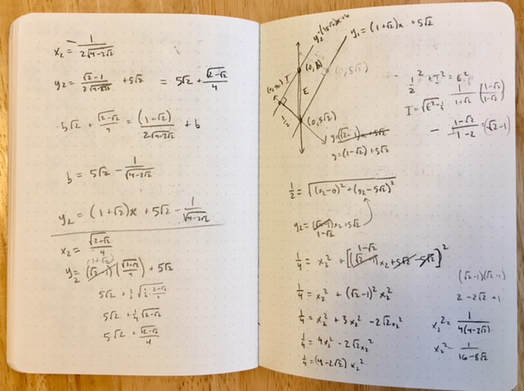
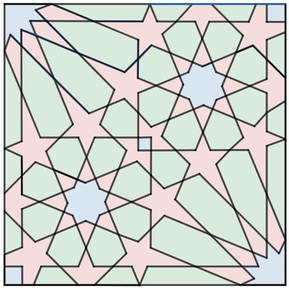
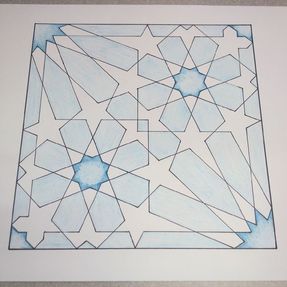
Mathy MomentsYou can see from my notebook below that some of the math took me a few tries (this goes on for several pages). To make the weave for the 8 fold rosette, I made lines parallel to the original with a distance of 0.5 above and below. Each ribbon was then 1 unit wide. I was working with the equations in point-slope form. I'm pretty sure that there are more efficient ways to do these calculations but I haven't discovered them yet. I really like how these messy bits encourage me look for more efficient and elegant methods. Desmos Geometry ToolAfter working with the Desmos calculator for a while, I wanted to give the geometry tool a try. I decided to try a pattern that I saw on the Pattern In Islamic Art website. This site has some great resources. The pattern that I tried was from David Wade's book Pattern in Islamic Art. The geometry tool requires much less algebraic manipulation, but I find hiding the underlying grid is much more tedious than in the calculator. Everything has to be hidden individually instead of turning a whole folder on or off in the calculator. I've drawn this pattern in the past by hand and it would have been much more difficult if I didn't have that previous experience. Future ProjectsI've tried tiling some designs to cover the plane but I haven't come up with any good methods for this yet. I've also tried using sliders to dynamically adjust some of the relationships between the sizes of the pieces in these designs. These are great challenges and are helping me learn new features of Desmos. Dan Meyer wrote "If Math Is The Aspirin, Then How Do You Create The Headache?" I hesitate to call these graphing projects "headaches" because I enjoy the challenge. Regardless, this is a case where my need for mathematical solutions guide my learning and give me reasons to explore new graphing methods. EL
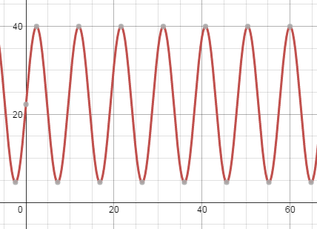
Revisiting the Classic Ferris Wheel Problem
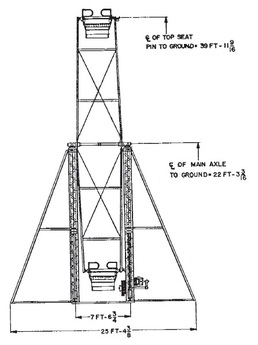
This type of pseudo-context word problem robs students of the opportunity to explore and analyze real-world problems in much depth. Dan Meyer has written quite quite a lot about pseudocontext. My concern with the Ferris wheel problem is not that you can't model the height of a seat on a Ferris wheel with a sine function, it is why would you do it? Instead of doing a textbook problem with a fictional Ferris wheel, I decided to use a real Ferris wheel from a nearby amusement park that some of my students would be familiar with. I visited the park to take a video of the Ferris wheel in action. Below is a 30 second clip of the "Big Ellie" Ferris Wheel at Atlantic Playland. Notice and WonderI started by asking students what they noticed in the video. After brainstorming and recording the students observations I asked students what they wondered about in the video. They asked questions like "how fast is the ride going?", "how tall is this Ferris wheel?", "how far can you see from the top of the ride?", "how long does the ride last?". In order to investigate these questions further we needed to estimate some values such as the radius of the wheel, how long it takes to make one revolution, and the height of the central axis about the ground. I asked students to estimate these values using the clues in the video we watched. We watched it several times in order to get some good estimates. I also talked about some of the mental math required to operate a ride like this. Because it is belt driven, you have to load the Ferris wheel so that it is equally balanced around the wheel. Otherwise, one side of the wheel would become too heavy and the drive cable would slip in the rim and the wheel wouldn't be able to turn! This requires a lot of on the fly estimates of weights of the riders as it is being loaded. In order to get a see how good we did with our estimations we turned to the internet in order to try to hunt down some of these values with a Google search. This lead to a discussion about what keywords we could use to hunt down this information. A search of "height of the central axis of the Ferris wheel at Atlantic Playland" was not very fruitful... an essential skill to solve a problem like this is to translate mathematical language into common terms that you can use for a Google search. Ve Anusic has a great blog post where he discusses a similar problem and the discussion with his students about the information you need and the information you might find online. First we did a search to find Atlantic Playland's website and found that they called their ride "Big Ellie". A search for this name lead us to believe that this Ferris wheel is a No. 5 Big Eli wheel made by Eli Bridge (I later emailed the park and confirmed that this is indeed the model of their Ferris wheel). Eli Bridge's website gave us some interesting information but not exactly what we were looking for. A bit more searching and we were able to find a pdf of the owner's manual for this ride that included a helpful diagram.
It is only after we were able to answer some of the students' questions regarding the video of the Ferris wheel did we start to talk how we might mathematically modeling the height of a person riding the wheel over time and the periodic nature of this function. Students were much better able to make sense of this visual model once they had a good grasp of the context of the problem.
Nova Scotia Mathematics Curriculum Outcomes Mathematics 12 - RF03 Represent data, using sinusoidal functions, to solve problems. Pre-calculus 12 - T04 Graph and analyze the trigonometric functions sine, cosine and tangent to solve problems. EL
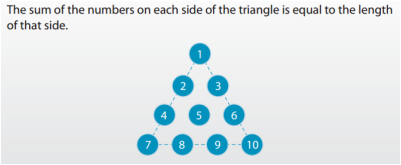
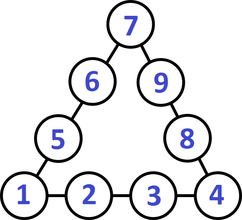
The final chapter of the Math at Work 12 textbook deals with Trigonometry and the Law of Sines and Law of Cosines. Towards the end of the chapter there is a puzzle (p351) that asks students to create a triangle using 9 of the numbers from 1 to 10. Each side of the triangle is the sum of 4 of these numbers. I liked the construct of this puzzle but I wasn't a big fan of the questions that it asked students so I decided to give it an overhaul. An image from the textbook is below.
We followed up this warm-up with an open middle style problem using the same situation that would require students to apply the law of cosines. A challenge like the one below gives the students a reason to practice the law of cosines without feeling tedious or repetitive. Directions: Use the numbers 1-9 (using each number no more than once) to fill in the circles. The sum of the numbers on each side of the triangle is equal to the length of that side. What is the triangle with the largest (or smallest) angle that you can make? Hints:
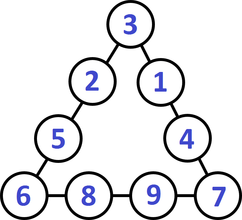
A triangle with the largest angle (there are several variations with the same angle): Side A: 6+8+9+7=30 Side B: 7+4+1+3=15 Side C: 3+2+5+6=16 Angle A: 150.799 Angle B: 14.119 Angle C = 15.082 A triangle with the smallest angle (there are several variations with the same angle): Side A: 1+2+3+4=10 Side B: 4+8+9+7=28 Side C: 1+5+6+7=19 Angle A: 10.844 Angle B: 148.212 Angle C = 20.944
Another challenging question that could be asked is how many different arrangements of the numbers 1 to 9 in the triangle diagram could you make? You have to consider that rotations of the triangle are the same. This would be a challenging combinatorics question even for Pre-calculus 12 students. Nova Scotia Mathematics Curriculum Outcomes Mathematics 11 - G03 Solve problems that involve the cosine law and the sine law, including the ambiguous case. Math at Work 12 - G01 Students will be expected to solve problems by using the sine law and cosine law, excluding the ambiguous case. Math at Work 12 - N01 Students will be expected to analyze puzzles and games that involve logical reasoning, using problem-solving strategies. Mathematics 12 - LR01 Analyze puzzles and games that involve numerical and logical reasoning, using problem-solving strategies Pre-calculus 12 - PC03 Determine the number of combinations of n different elements taken r at a time to solve problems. EL
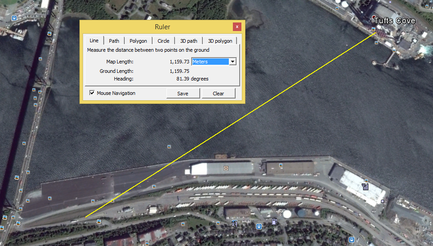
What is the tallest man-made structure around Halifax? Ask students to brainstorm a few ideas. Students might suggest a tall building. Some of the tallest buildings around Halifax are the Maritime Centre 78 m (256 ft), Purdy's Wharf 88 m (289 ft) and Fenwick Tower, the tallest building in Halifax at 98 m (322 ft) tall. Students might also suggest one of the two harbour bridges. The towers on the MacDonald Bridge are 103 m (338 ft) high and the towers on the MacKay Bridge are 96 m (315 ft). The towers on the MacDonald bridge are taller than the tallest buildings in Halifax. An observant student might even suggest the red and white painted smokestacks at the Tufts Cove Generating station. The smokestacks are tall indeed. From the picture below, you can see that the smokestacks are taller than the bridge towers of the MacKay Bridge. You might ask students how you know by looking at the picture that the smokestacks are taller than the bridge towers. This would be a fun opportunity to talk about perspective. We can check out the height of the smokestacks by using a little trigonometry. I found a spot across the harbour from Tuft's Cove to measure the angle to the top of the smokestacks using a clinometer. (My favourite school/education clinometer is the Invicta MK1 Clinometer... not only does it have a cool name, it looks really cool as well!) It was an angle of elevation of 8 degrees. Next I used Google Earth to see that my distance to the centre stack is approx. 1160 metres. So that means tan(8) = x/1160. Solving for x gives us x = 1160*tan(8) = 163 metres. I emailed Emera an they said that the stacks are actually 500 ft. (152.4 m) tall. So I'm about 11 metres off. Not bad considering that at this distance, a variation of 1 degree is about 20 meters. The actual angle should have been about 7.5 degrees vice 8 degrees. So, how could I minimize the amount of error? As I get farther away, the tangent value gets smaller but the distance that I'm multiplying by gets bigger. At what angle does 1 degree of error create the least amount of difference in the height being measured? But is this the tallest man-made structure in Halifax? I used to think so, but I was only considering free standing structures. There is a radio transmission tower that is taller but not free standing... the tower has guy wires to hold it up. The CBC radio tower on Geizer’s Hill is even taller than the smokestacks at Tuft's Cove. So how tall is this tower? I drove up to the top of Geizer's Hill to find out. I found a spot level to the base of the tower at a distance of 475 meters along Washmill Lake Dr. From this spot, my clinometer measured an angle of inclination to the top of the tower of about 23 degrees. 475 x tan(23) = 201 meters (about 659 ft). A bit of digging led me to a website that stated the antenna height above ground level for the CBC radio tower is 192 m (629 ft). My measurement was only 9 meters different from this height... pretty close. This is so far the tallest thing I've found around Halifax. Let me know if you find something taller!
EL |
Categories
All
|
||||||||||||||||






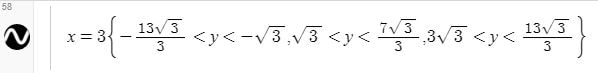

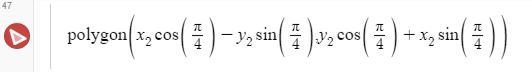







 RSS Feed
RSS Feed