|
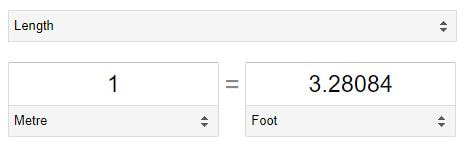
Swimming in the hotel pool I saw these depth markers. As a math teacher, they made me a bit uneasy. What do you notice in the photos below? What do you wonder? Just look at those significant digits. They look so precise. I first thought... going from the shallow end to the deep end, it gets 1 foot / 0.2 metres deeper. That must mean that 1 ft = 0.2 m right? But then if 1 ft is 0.2 m then shouldn't 3 ft in the shallow end be 0.6 m instead of 1.0 m? So I looked at it another way... 1 m is the same as 3 ft... So 1 ft must be about 0.33 m. Which would make 4 ft equal to about 1.33 m not the 1.2 m as shown. But I know that a meter stick is shorter than a yard stick so this is just an approximation. No problem, they just rounded off both values. Then I had a moment of doubt... in the shallow end the values are in a ratio of 1/3 and in the deep end the values are in a ratio of 4/12 which is also 1/3 so shouldn't this work out? Then I realized the errors and misconceptions in this line of thinking.
Other Linear ConversionsToday, as I was driving around, I looked more closely at the clearance signs that I passed under. There doesn't seem to be much consistency in the units used or precision. Do people with tall cars know the height of their car? I just know that I'm about 6 ft tall and my car is shorter than I am. Of course you can always just wing it. If you clear the warning bar, you're good to go. Anyway, I know for sure that my car is less than 11 foot 8 if I ever end up in North Carolina.
I saw this relatively accurate sign at a parking garage today so I took a photo. 6'0" is approximately 1.8288 metres so these values are the closest I've seen. Nova Scotia Mathematics Curriculum Outcomes Mathematics 10 M02 - Students will be expected to apply proportional reasoning to problems that involve conversions between SI and imperial units of measure. Mathematics at Work 10 M01 - Students will be expected to demonstrate an understanding of the International System of Units (SI) by describing the relationships of the units for length, area, volume, capacity, mass, and temperature and applying strategies to convert SI units to imperial units. Mathematics Essentials 10 D1 - Demonstrate a working knowledge of the metric system and imperial system. EL
A couple of weeks ago, I saw a tweet from Don Fraser (@DonFraser9) in which he noticed that every box of Raisin Bran says "2 scoops" no matter what it's size is. I was recently talking with a teacher about the Percent, Ratio, and Rate unit for grade 8 math and I was reminded of Don's question. This deserved some additional investigation so I headed to the grocery store to gather the facts. At my local store, Kellogg's Raisin Bran is available in 3 sizes as seen below. Questions to Consider1. Rate: Which size box of cereal has the best unit price (g/$)? 2. Ratio: If there are two scoops in the regular size box, to preserve the same proportion of raisins, how many scoops should there be in the Family Size and Jumbo Size box? Alternatively, if the ideal proportion of raisins is to be found in a different size box, how many scoops should there be in the other two sizes? 3. Ratio: A "scoop" is a non-standard unit of measure. If the amount of raisins in each box stays the same proportion, then how should the size of the scoops change in order to maintain that proportion in each size box? 4. Volume: These boxes all have different volumes. Determine the volume of each and compare it to the weigh of cereal in that box. Does this rate stay the same? If it doesn't, what does it tell you about the amount of empty space in the box? How do the dimensions of each box compare? Are the different sized boxes similar shapes? Some additional Raisin Bran resources: Nova Scotia Mathematics Curriculum Outcomes Grade 8 M03 - Students will be expected to determine the surface area of right rectangular prisms, right triangular prisms, and right cylinders to solve problems. Grade 8 M04 - Students will be expected to develop and apply formulas for determining the volume of right rectangular prisms, right triangular prisms, and right cylinders. Grade 8 N04 - Students will be expected to demonstrate an understanding of ratio and rate. Grade 8 N05 - Students will be expected to solve problems that involve rates, ratios, and proportional reasoning. Grade 9 SP03 - Students will be expected to develop and implement a project plan for the collection, display, and analysis of data by: formulating a question for investigation; choosing a data collection method that includes social considerations; selecting a population or a sample; collecting the data; displaying the collected data in an appropriate manner; drawing conclusions to answer the question. Mathematics 12 MRP01 - Research and give a presentation on topic that involves the application of mathematics. EL
Here are a few questions that I thought about:
Below are some additional photos: Given the list of lego bricks, you could ask students a number of additional questions:
The Discovery Centre is currently working on a project to build Canada's largest Lego mosaic wall. The wall will be installed at the Discovery Centre's new location when it moves. Nova Scotia Mathematics Curriculum Outcomes Mathematics 7 - N07 Students will be expected to compare, order, and position positive fractions, positive decimals (to thousandths), and whole numbers by using benchmarks, place value, and equivalent fractions and/or decimals. Mathematics 8 - N03 Students will be expected to demonstrate an understanding of and solve problems involving percents greater than or equal to 0%. Mathematics 8 - N04 Students will be expected to demonstrate an understanding of ratio and rate. Mathematics 9 - N03 Students will be expected to demonstrate an understanding of rational numbers by comparing and ordering rational numbers and solving problems that involve arithmetic operations on rational numbers. Mathematics at Work 11 - G02 Students will be expected to solve problems that involve scale. EL
My wife and I were enjoying a peanut butter cup after dinner a few nights ago. She was eating a standard peanut butter cup (wide and short) and I was eating a miniature peanut butter cup (narrow and tall). I mentioned that the economy rate of mine was higher than hers and therefore my peanut butter cup had a higher peanut butter to chocolate ratio (the economy rate of a container is the ratio of its volume to its surface area. The higher the ratio, the more economical the container is). A 'lively discussion' ensued with a few pauses for the rolling of eyes. Time to break out a ruler, calculator, and the formula for the volume of a frustum (a truncated cone or pyramid) which is the shape of a peanut butter cup. The volume of a frustum is given by the following formula: where R and r are the radii of the top and bottom circles of the truncated cone. The formula can be derived without calculus by taking the entire cone and subtracting the tip to make a frustum. When Heron of Alexandria derived the formula for the volume of a square based frustum, he created the the Heronian mean. The Heronian mean of two numbers A and B is the weighted mean of their arithmetic mean and geometric mean. With this, he was one of the first people to encounter imaginary numbers. The formula below is the general formula for a frustum where A and B are the upper and lower base of the frustum: Lets find the total volume of the big peanut butter cup first. R = 46 mm, r = 38 mm and h = 10 mm. Therefore the volume is 55585.25 mm^3. If we assume that the chocolate is a uniform thickness of 1 mm then we can easily calculate the volume of the peanut butter by subtracting 2 mm from each measurement and recalculating giving 40346.43 mm^3. That means that the volume of chocolate is the difference of these two values or 15238.82 mm^3. This gives us a peanut butter to chocolate ratio of 2.65 Now time to measure the little peanut butter cup. R = 27 mm, r =22 mm and h = 14 mm. Given these measurements, the total volume is 26492.00 mm^3, the volume of peanut butter is 19163.72 mm^3 and the volume of chocolate is 7328.28 mm^3.
This gives us a peanut butter to chocolate ratio for the little peanut butter cup of 2.61. Nearly identical. But the thickness of the chocolate is far from uniform as this cross section shows. The chocolate is actually quite a bit thicker on top and bottom of the little peanut butter cup than on the big one. The peanut butter in the little peanut butter cup actually looks closer to a half-sphere than a frustum. So if you love the chocolate you should eat the little peanut butter cups and if you love the peanut butter, you should eat the big peanut butter cup. EL |
Categories
All
|















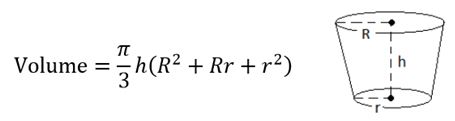
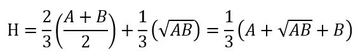


 RSS Feed
RSS Feed