|
Brian Bolt has written numerous resource books for teachers containing collections of rich mathematical problems, puzzles, investigations and games. Some are descriptions of classic problems and puzzles while others are new creations. I think these books are a great resource and I wanted to share three of my favourite problems from them. Number the Sectors
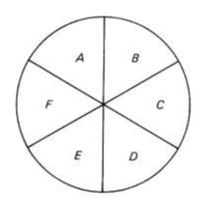
This is problem #53 from Even More Mathematical Activities (1987) and problem #72 from The Mathematical Funfair (1989). Instead of starting by asking students to find a set of numbers that gives all the integers from 1 to 25, I like to create an example as a class and then challenge them to do better (get to a larger number). You can also ask them to prove what the maximum value is. Bolt has an alternate version of this puzzle in A Mathematical Pandora's Box (1993) (#12 Can you Do Better), which has 5 sectors around a central circle. This version can be found online at NRICH Maths as the Number Daisy. How Large a Number Can You Make?Make the largest number with just the digits 1, 2, and 3 once only once and any mathematical symbols you are aware of, but no symbol is to be used more than once. The challenge is to see who can make the largest number. Here are some numbers to get the ball rolling: This is problem #83 from Even More Mathematical Activities, (1987). I've given this as a warm-up problem for high school students and this often leads to a discussion of how to know which is bigger, 2^(31) or 3^(21)? Make a CenturyPut arithmetical signs in suitable places between the digits to make the following sum correct: 1 2 3 4 5 6 7 8 9 = 100 There is more than one solution. See how many you can find. This is problem #127 from Mathematical Activities (1982). I would start this challenge with students by asking them to make an expression using the numbers from 1 to 9 to make a value as close as possible to 100. I would then add on the challenge to try to find an expression exactly equal to 100. There is a very similar problem called Make 100 on NRICH Maths. I saw an earlier version of this as problem #94 in Amusements in Mathematics (1917) by Henry Ernest Dudeney. In Dudeney's version, he includes an additional challenge to try to find a solution which "employs (1) the fewest possible signs, and (2) the fewest possible separate strokes or dots of the pen. That is, it is necessary to use as few signs as possible, and those signs should be of the simplest form. The signs of addition and multiplication (+ and ×) will thus count as two strokes, the sign of subtraction (-) as one stroke, the sign of division (÷) as three, and so on." What are Your Favourite Problems?Do you have a favourite problem or puzzle from one of Brian Bolt's puzzle books? Do you have other favourite collections of puzzles? EL
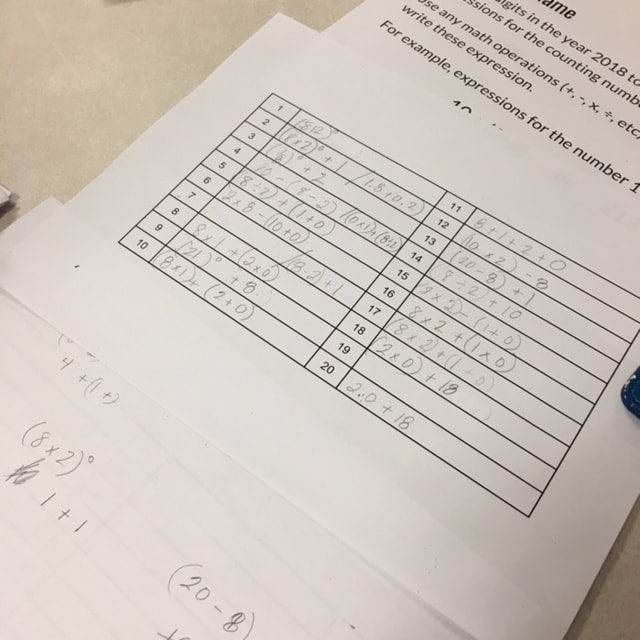
During a professional development session today with grade primary to grade 9 math coaches and support teachers, we spent some time working on solving some math puzzles. We used our work on these puzzles to reflect on what good group work looks and sounds like. We also discussed the characteristics of effective mathematical communication. It was great to see positive energy and teachers supporting and encouraging each other. Below are the five math puzzles and investigations that we worked on. We selected these puzzles because they are easy to explain, open to a wide range of students, and offered a fun challenge. 1-10 Card InvestigationThis problem from Marilyn Burns asks you to find a special order for a stack of cards, Ace through 10. Place the stack of cards face down and turn over the first card. It should be the Ace. Place the next card on the bottom of the deck and then reveal the top card. It should be the number 2. Continue placing the next card on the bottom of the deck and then revealing the top card until all the cards are revealed. The face up cards should now be in order from Ace to 10. Marilyn recorded a video to demonstrate these rules that is much easier to understand than my written instructions. Marilyn's has a description of this problem on the MathSolutions website. This logic problem doesn't rely on any prerequisite mathematical knowledge and you can try it out quickly to see if you've come up with the correct solution. It gives students a chance to work together to try out strategies. The Square-Sum ProblemCan you order all the numbers from 1 through 15 so that the sum of any two consecutive numbers are always a square number? For example, in the sequence: 4, 5, 11; 4+5=9 and 5+11=16.I really like this problem because there are some great extensions to take this problem farther and there is a very nice way to visualize the possible solutions. Numberphile has recorded a great video demonstrating both the problem and solution. The Year Game - 2018Use the digits in the year 2018 to write mathematical expressions for the counting numbers 1 through 100 (we only went to 20). Use any math operations (+, -, x, ÷, etc) and parentheses to write these expression. There is a more detailed description of this problem at the Math Forum website. For example, expressions for the number 1 might be: 10 ÷ (2+8) or 218^0. This problem is very similar to the classic Four Fours problem but with new digits each year. Which numbers are the hardest to find an expression for? Why do you think this is? I think this problem also leads nicely to a discussion about mathematical elegance and beauty. Look at a variety of expressions with the same value. Which expression do you think is the best? What makes for an "elegant" solution? Perimeter 12This problem challenged groups to make as many different shapes as possible with a perimeter of 12 units using a geoboard (or dot paper). Shapes were recorded on dot paper to make sure no shapes were repeated as reflections or rotations. I've seen variations of this problem in several places. One of them is Brian Bolt's book Mathematical Activities (1982). He suggests not only to find shapes with a perimeter of 12 but to also find the area of each shape. You can then find which shape has the maximum/minimum area. He also challenges students to find non-rectangular shapes (e.g. triangles) with a perimeter of 12 units. There were some good discussions about the lengths of diagonal line segments on the geoboard. Eight DominoesThis problem is from NRICH. Finding a solution took some perseverance but most groups were eventually successful. The problem challenges you to create a square using 8 specific dominoes (0-1, 0-2, 0-3, 0-6, 1-2, 1-4, 2-2, and 3-5). In the 4 x 4 square, each of the columns and rows should sum to 8. The 3-5 domino seemed to be key as the rest of the squares in that row (or column) had to be blank. What are your favourite math or logic puzzles? EL
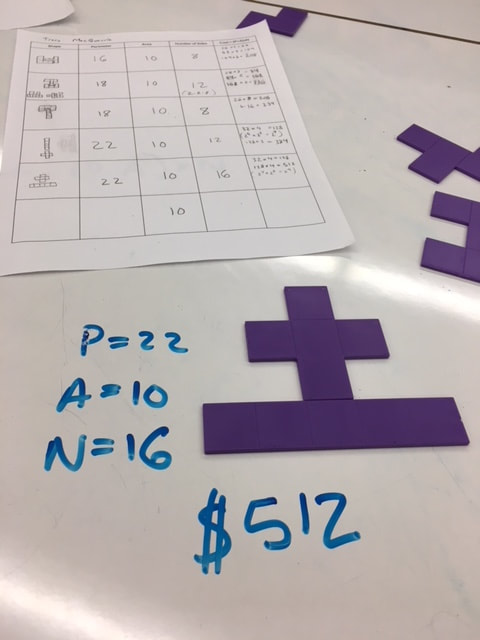
An engaging puzzle with simple instructions is to ask students to create a rectangle using pentomino pieces. Let them figure out what rectangle dimensions are possible given the total number of squares in the pentominoes they're using (for a full set of 12 pentominoes, 3x20, 4x15, 5x12 and 6x10 are possible). You can also print off a variety of other shapes and challenge students to fill those shapes with pentominoes or have students create their own shapes and challenge their friends to solve them. Younger students can be challenged to fill an empty picture frame or tray with pentominoes. Here are five great games, puzzles and activities (in no particular order) that use pentominoes:
2. Pentomino Puzzles from Jon Orr (@MrOrr_geek) - Jon describes an activity where students are given a hundreds chart and a transparent pentomino. Ask students to place their pentomino on the hundreds chart so that it covers a sum of 135. Then ask students to share their strategies for finding the correct placement. Are there sums that are not possible to achieve? Continue the activity by selecting different tiles, giving different sums to find, creating equations and solving them. I also saw these questions posted by Amie Albrecht (@nomad_penguin) on twitter, "Can you find a pentomino that covers numbers that: sum to 150, sum to an even number, covers three multiples of 4, and more". Jon created an online Desmos Activity that allows you to do this activity virtually. 3. Pentomino Farms - I was introduced the the pentomino farms activity from Martin Gardener's book Knotted Doughnuts and Other Mathematical Entertainments. The task is to use the 12 pentominoes to build a fence around a field on your farm. The rule used to join the pentominoes to form a fence is that they must touch along the full edge of a square and not just at the corners. There are four types of farms to create. For each type, what's the largest field you can enclose?
4. How Convex is a Pentomino? - Which pentomino shape is the most convex? How do you measure "convexity"? This is an interesting question that generated lots of discussion on Twitter. Some interesting methods of measuring this were discussed by Alexandre Muñiz (@two_star) in his blog post, "Vexed by Convexity." I think it would make a great discussion for students to rank the pentominoes by convexity and then defend their choices.
If you have a favourite activity, puzzle or game featuring pentominoes, I would love to hear about it! EL
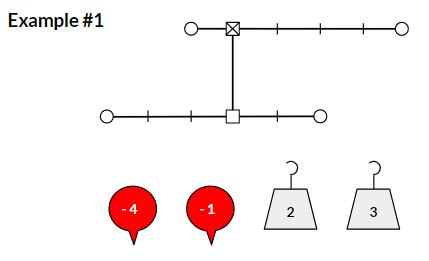
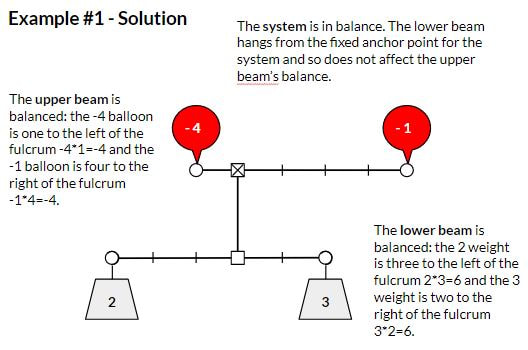
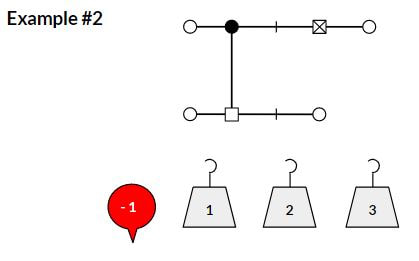
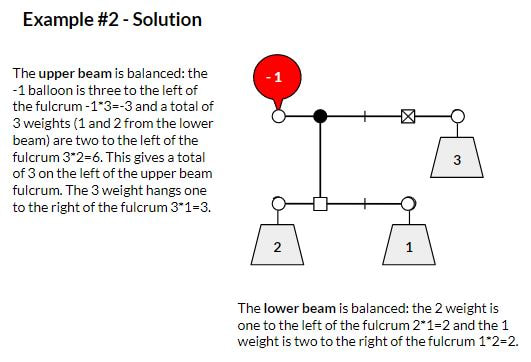
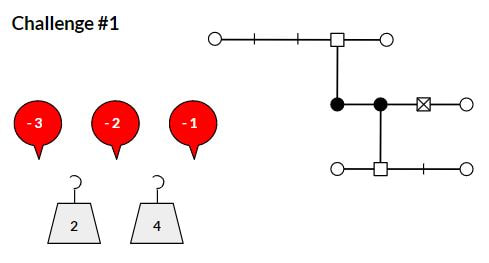
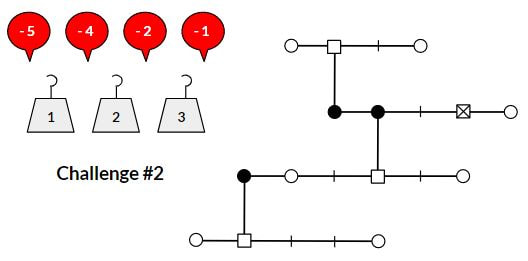
I recently stumbled across Richard Garfield's Balloon Balance puzzle from the 9th World Puzzle Championship in October, 2000. The puzzle is similar traditional balance puzzles such as SolveMe Mobiles but with a couple of twists. The first twist is the use of balloons to include negative numbers. The second twist is the inclusion of torque... the farther from the balance point (i.e. fulcrum), the more force is applied. I thought that a simplified version of this puzzle might work well for students who are practicing integer multiplication. First however I had to figure out the puzzle. I have to admit that this puzzle took me quite a while to solve and make sense of. I almost gave up a couple of times but I eventually figured it out. Solving this puzzle reminded me of how it feels to be a learner and to empathize with students struggling to understand a new concept. If you'd like to see the solution to the puzzle above, click this link. To use this with students, I simplified the puzzle a bit and then made some examples and easier challenges to start with. I modeled these from a version of this puzzle created by Joseph DeVincentis for the Boston Area Puzzle Hunt League (BAPHL) #5. Directions: On each set of balances, place the given balloons and weights in the open circles. Each beam should be balanced around its fulcrum (the small square) by the torque rule: sum of weight times distance from fulcrum for all weights on the left should equal that on the right. The beams themselves are weightless. The fulcrum with an x is the fixed anchor point for the system. The first example shows students how the basic puzzle works. The second example below add additional complexity to the system while retaining only 4 weights/balloons to place. I created two challenge puzzles for students to work on once they were confident with the examples. I haven't tried this out with students yet so I'm not sure what to expect. Feel free to check out my Google Slides with the examples, challenges and solutions. I'd appreciate feedback if you have suggestions to improve this. Nova Scotia Mathematics Curriculum Outcomes Grade 8 N07 - Students will be expected to demonstrate an understanding of multiplication and division of integers, concretely, pictorially, and symbolically. EL
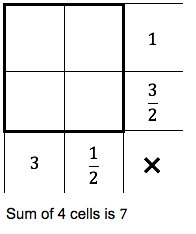
Practice is important. Whether it is playing the piano, shooting free-throws, popping an ollie or solving a quadratic equation you need to practice to improve. Some practice routines are more effective than others at helping students solidify their understanding. Practice can often seem tedious and it can be difficult to maintain the motivation to practice. In mathematics, students practice skills in a variety of ways. One style of practice that can help students stay motivated and engaged is purposeful practice. Instead of a page full of repetitive problems, students focus on an activity that has a mathematical goal to achieve. Dan Meyer wrote a blog post a few years ago titled "Purposeful Practice & Dandy Candies" that started me thinking about how to make activities in my classroom more purposeful. Open MiddleOne of my favourite sources of problems with purposeful practice is Open Middle. There is a large selection of questions organized by topic and grade level. Each question has an "open middle" meaning there are many ways to explore and solve the problem. Below is a question submitted to the Open Middle site by Robert Kaplinsky. In this question, students try to find the arrangement of digits that yields the product closest to 50. Students will try numerous different arrangements of digits and get lots of practice multiplying decimal numbers without it seeming tedious. The question can also be quickly modified to give additional practice. For example, just add a hundredths place onto one of the factors and use 5 different digits. Math GamesGames can be a great way to encourage students to practice. There are lots of examples of but I'm going to mention just two. The first goes by several names. Joe Schwartz wrote a great post about Factor Captor. A similar game is described on the NCTM Illuminations site called the Factor Game. Students alternate turns playing on board filled with numbers. The first player selects a number to cover and adds that number to their score. The second player finds all the factors of that number, covers them and totals those number to add to their score. The roles are then reversed and play continues until there are no uncovered numbers remaining. There is a lot of math in this game and it is fun to play. The second game is Horseshoes from Math4Love. This game is played with a deck of cards numbered 1-9. Two cards are drawn to form a two-digit target number. Then four more cards are drawn. Players use these four digits to create an equation using addition and subtraction that is as close as possible to the target number. For example, let's say that the target number is 25 and the four digits given are 1, 3, 6 and 9. A student might create the equation 39-16 = 23. Another student might make the equation 13+6+9 = 28. There are lots of way to tweak this game for different levels of complexity. Both of these games allow for lots of numerical practice in a format that engages students. There are many excellent sources of ideas for mathematical games. My current 'go-to' resource is a book titled Well Played, 6-8. Math PuzzlesThere are several mathematical puzzles that include lots of practice with numerical computations in pursuit of a solution. KenKen puzzles and Maze 100 from NRICH are two such puzzles that I've used. I also think that Yohaku puzzles are great. They are numerical puzzles where you need to determine the number that is in each square in order to make the column and row sum/products.
Desmos ActivitiesFor classrooms with the available technology, activities from Desmos.com are another way to practice with purpose. An activity that incorporates a lot of meaningful practice is Marbleslides. In this activity, student try to capture stars on a Cartesian grid by creating a path using functions that marbles roll down. Students work to refine their functions to capture as many marbles as possible. Another activity that generates lots of practice is Transformation Golf. Students use a series of rigid transformations to move a shape to specified location. They have to find an efficient path around several obstacles. Each successive challenge increases in complexity. IncentivesThere are also activities that have a non-math goal for students to achieve. Lots of online math games have incentives for students such as badges to earn, experience points to accumulate or virtual prizes to win. There are also worksheets and activities with non-math goals. Worksheets such as "Algebra with Pizzazz" and "Punchline Algebra" have a riddle to be solved once all of the questions are completed. In my classroom practice, I used a number of activities with these types of incentives and I think that many students find them exciting and fun. If students are excited to do math, I consider that a win. However, I think that these types of activities should be used with caution. We don't want to inadvertently send a message to our students that math isn't fun by itself so we have to disguise it (like sneaking vegetables into their favourite foods so kids will eat them). Please Share!If you have a favourite math activity, game or puzzle that gets students practicing math with a purpose, I'd love to hear about it. Please leave me a comment. EL
Activities that let students get immediate feedback on how their are doing are extremely beneficial. Activities that allow students to self-check their own work allow for this immediate feedback and correction. These types of activities can allow the teacher to focus their time with students who are having conceptual misunderstandings and not get bogged down helping students find and correct computational errors. While students are engaged in self-checking activities, the teacher can also be working with small groups of students on mini-lessons or conversations/conferences. Below are a few of my favourite activities and routines that allow for students to check their own work: Team Post-Its - I recently saw this activity described in a post by Julie Morgan. This activity is very easy to set up and does not require much front loaded time to create. The teacher posts a list of questions for small groups of students to work on. These might even be questions from the textbook. Each group solves the question, writes their answer on a sticky note and posts it on the whiteboard. As other groups complete the questions, they can compare their answers to those from other groups to see if they agree. If they don't agree, they double check their work. I would suggest that each group of students starts with a different question. Add ‘Em Up - In this activity, students do a set of problems, either on their own or as a group. These problems typically have numerical answers. The answers to the set of problems are added up and compared to the sum provided. If the sum is not the same, then the student knows that one or more of the problems in the set was done incorrectly and works to find the error. I first saw this activity described in a blog post from Kate Nowak. I later saw a blog post from Amy Gruen describing a simple and quick way to do this same activity that I used occasionally. There are many descriptions of how to organize this activity including one in a detailed blog post from Sara VanDerWerf. Row Game - I also first saw this activity described in a blog post from Kate Nowak. Typically, a row game is a worksheet of problems organized in two columns. The worksheet is completed by a pair of students, one doing the problems in column A and the other doing the problems in column B. The problems in each row have the same answer so if the students' answers don't match, they can work together to check their solutions to find the error. To make row games a bit easier to create, you can create an additional column with the sum of the solutions from column A and B (similar to the Add 'Em Up activity from above). This allows you to use any two problems and not have to create two problems with the same solution. Kate Nowak has a shared google folder with a large selection of crowd-sourced row games. Added 03Oct017 - I recently saw a great idea from Heidi Neufeld. She asked students who finished quickly to make a new row for the row game and create two different problems with the same answer.
Mathematical Circuit Training / Around the World / Star Chain / Question Stack - There are lots of different names for and variations of this activity. The essential part is that there is a series of problems and the answer for each problem leads you to the next question to ask. The answer to the final question leads you back to the starting question. This activity can be organized as a simple worksheet, a stack of cards to turn over, a set of cards to chain together or questions posted on signs around the classroom or hallway. If you make a mistake, you won't be able to find the next question and you know to try again. This can be done individually or in small groups.
Added 26Sep2017 - Thanks Alicia! Invisible Ink - The description of this activity is from a blog post from David Petro. Students solve a set of problems on a card. When ready, they can check their solutions using an answer card. This card has the correct answers written with "invisible" ink that can only be seen by shining a small UV light on it. Once the student has solve the questions correctly, they move on to the next card containing more complex questions. David says, "Students really seem to like this style of activity as they feel empowered to move from card to card when they are ready and the added feature of checking the answers with the UV pen gives a sense of novelty." If you know of any other self-checking activities that I've missed, please let me know and I'll add them here. EL
The Riddle of the Tiled Hearth is one of many mathematical puzzles from Henry Ernest Dudeney's 1907 book titled The Canterbury Puzzles And Other Curious Problems. The first group of puzzles in this book are based on the characters from Geoffrey Chaucer's Canterbury Tales. Puzzles from this book could be used as part of a cross curricular unit on history, literature and mathematics. There are a number of very interesting puzzles and games including the first pentomino puzzle called The Broken Chessboard and a clever variation of the game Nim called The Thirty One Game. Since this book was first published in 1907, the copyright has expired and it is freely available on Project Gutenberg. It seems that it was Friar Andrew who first managed to "rede the riddle of the Tiled Hearth." Yet it was a simple enough little puzzle. The square hearth, where they burnt their Yule logs and round which they had such merry carousings, was floored with sixteen large ornamental tiles. When these became cracked and burnt with the heat of the great fire, it was decided to put down new tiles, which had to be selected from four different patterns (the Cross, the Fleur-de-lys, the Lion, and the Star); but plain tiles were also available. The Abbot proposed that they should be laid as shown in our sketch, without any plain tiles at all; but Brother Richard broke in,-- To use this activity with students, I would start by introducing using the tiled hearth story as written above. Then I would introduce some manipulatives that would let them physically explore and work with the puzzle. I would give each group of students a large 4x4 grid on a sheet of paper and some multi-link cubes of 4 different colours.
One aspect of this puzzle that I like is that students can play around with it and have some intermediate success. They might just place a few cubes on the grid. With time, they can refine their solutions to get better and better. Below shows how a student might explore to place more and more cubes. The Solution from Canterbury Puzzles shows that the best solution leaves 3 blank spaces. Dudeney states, "The correct answer is shown in the illustration on page 196. No tile is in line (either horizontally, vertically, or diagonally) with another tile of the same design, and only three plain tiles are used. If after placing the four lions you fall into the error of placing four other tiles of another pattern, instead of only three, you will be left with four places that must be occupied by plain tiles. The secret consists in placing four of one kind and only three of each of the others." Below are both my solution using cubes and Dudeney's equivalent solution. EL
|
Categories
All
|
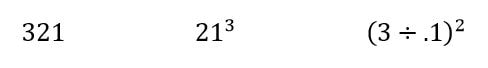

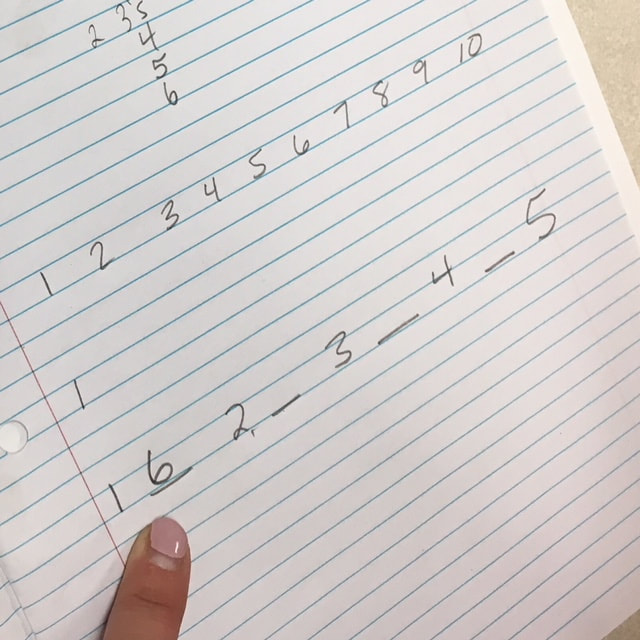


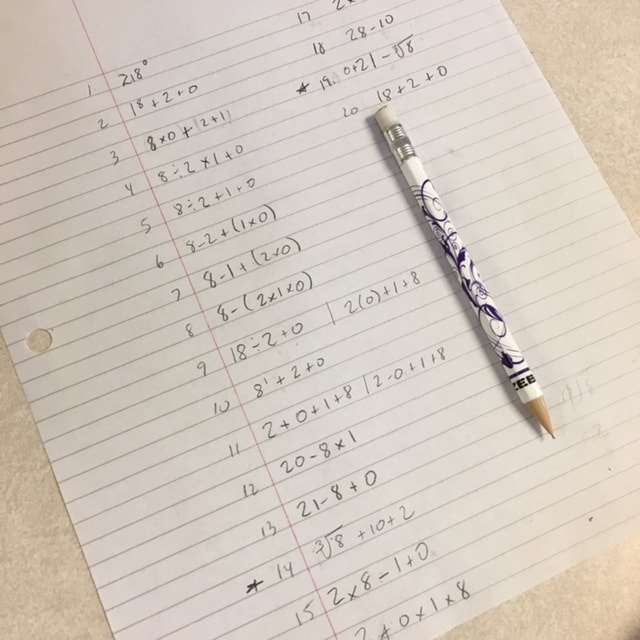

















 RSS Feed
RSS Feed