|
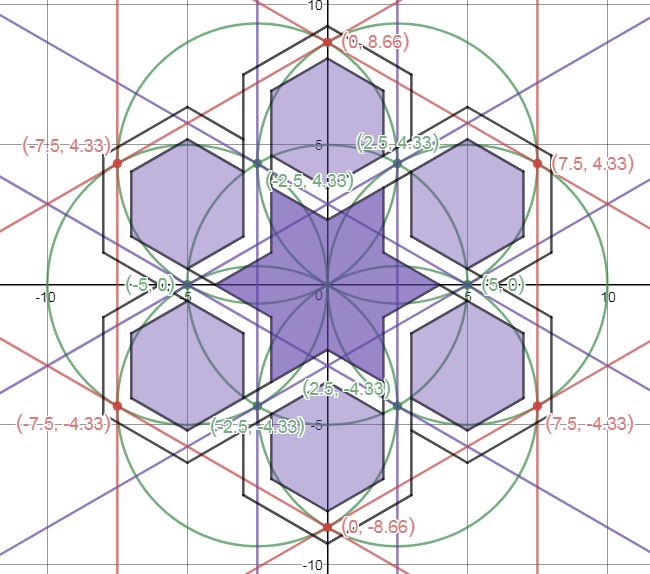
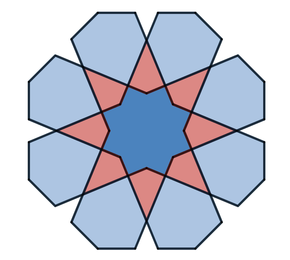
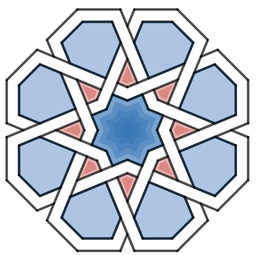
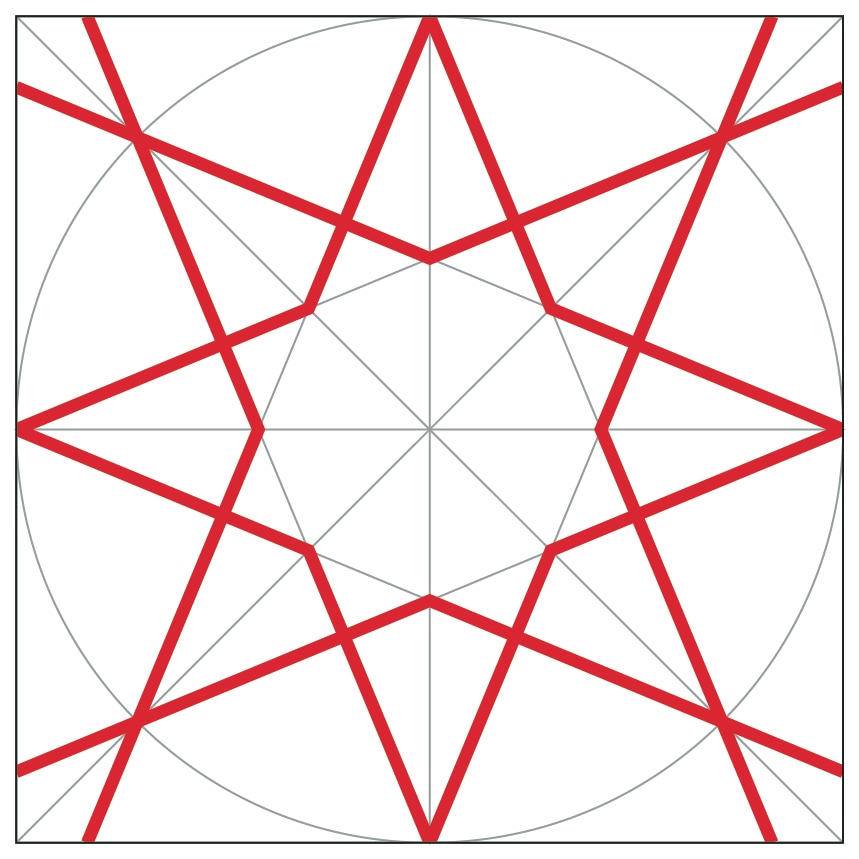
About a year ago, I signed up for Samira Mian's Udemy course on Islamic Geometry. I also purchased a copy of Eric Broug's book Islamic Geometric Patterns. I wanted to learn the basics so that I could determine if this might be a good way to satisfy the grade 7 mathematics geometric constructions outcome. I designed a short unit that I described last year. Recently, I decided to try replicating some of these patterns using the online Desmos calculator and geometry tool. I think having some experience drawing these patterns with a compass and straight edge was helpful. If you're looking for some Islamic geometric patterns to try, YouTube is a great place to get some ideas. There are some great instructional videos from Samira Mian and Nora Youssef, among others. The first pattern that I tried was a Star and Hexagon pattern that I learned from Samira's Udemy course. I learned that sticking with exact values are worth the effort. Rounding intersection points and slopes of lines to the nearest tenths or hundredths place work well at first but the errors compound and things start to get messy down the road. Interlacing the pattern gave me lots of practice with domain and range restrictions. 8 Fold RosetteNora Youssef has a nice video tutorial on for drawing an 8-Fold Rosette pattern. I did this pattern twice. The first time I constructed the basic pattern and the second time I added interlacing. I used the polygon function to add colour and figured out how to use trigonometry to rotate the polygons around the origin. This made it really efficient. I created a table with the vertices of the polygon and then just duplicated and rotated that polygon around the rosette. I duplicated the polygons multiple times to make the colours bold. Links:
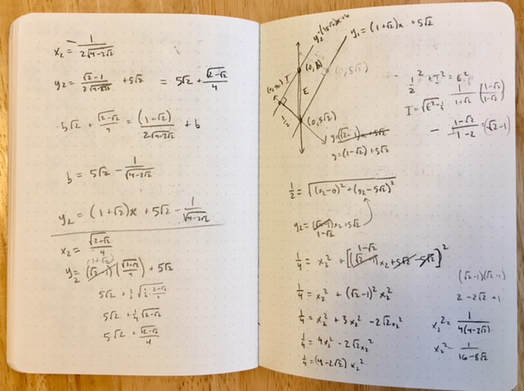
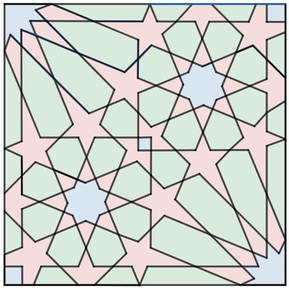
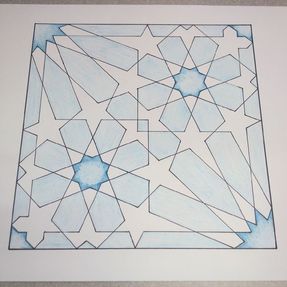
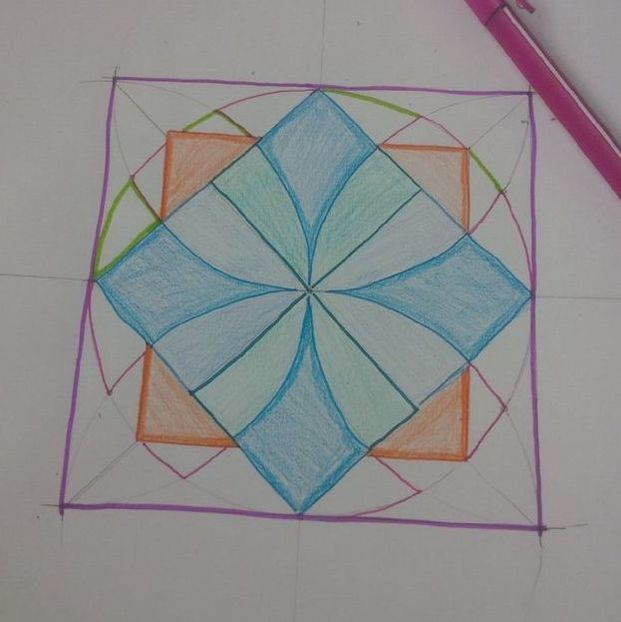
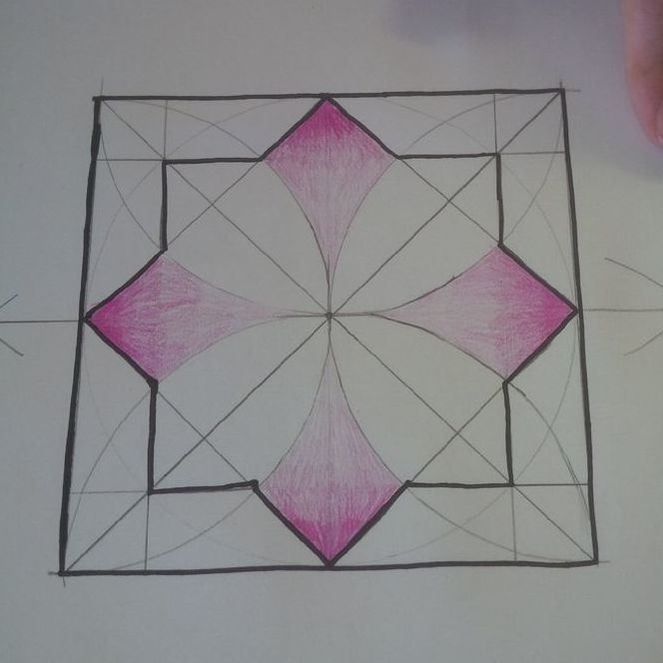
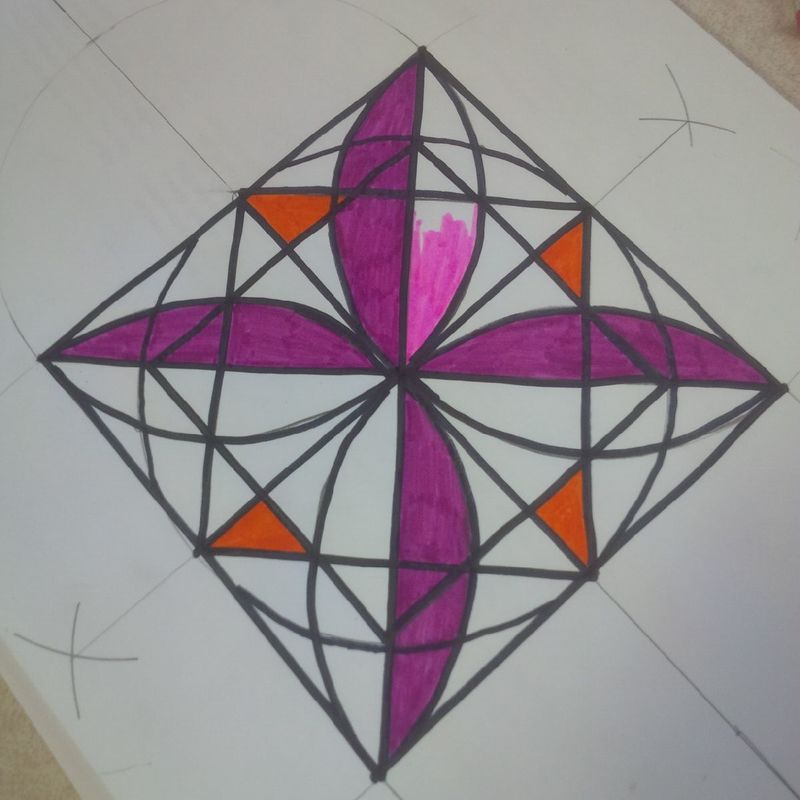
Mathy MomentsYou can see from my notebook below that some of the math took me a few tries (this goes on for several pages). To make the weave for the 8 fold rosette, I made lines parallel to the original with a distance of 0.5 above and below. Each ribbon was then 1 unit wide. I was working with the equations in point-slope form. I'm pretty sure that there are more efficient ways to do these calculations but I haven't discovered them yet. I really like how these messy bits encourage me look for more efficient and elegant methods. Desmos Geometry ToolAfter working with the Desmos calculator for a while, I wanted to give the geometry tool a try. I decided to try a pattern that I saw on the Pattern In Islamic Art website. This site has some great resources. The pattern that I tried was from David Wade's book Pattern in Islamic Art. The geometry tool requires much less algebraic manipulation, but I find hiding the underlying grid is much more tedious than in the calculator. Everything has to be hidden individually instead of turning a whole folder on or off in the calculator. I've drawn this pattern in the past by hand and it would have been much more difficult if I didn't have that previous experience. Future ProjectsI've tried tiling some designs to cover the plane but I haven't come up with any good methods for this yet. I've also tried using sliders to dynamically adjust some of the relationships between the sizes of the pieces in these designs. These are great challenges and are helping me learn new features of Desmos. Dan Meyer wrote "If Math Is The Aspirin, Then How Do You Create The Headache?" I hesitate to call these graphing projects "headaches" because I enjoy the challenge. Regardless, this is a case where my need for mathematical solutions guide my learning and give me reasons to explore new graphing methods. EL
June is here and the end of the school year in Nova Scotia is rapidly drawing near. In grade 7 math classes, it is time for students to break out their geometry sets and practice geometric constructions. The outcome for this unit (7G01) states, "Students will be expected to perform geometric constructions, including: perpendicular line segments, parallel line segments, perpendicular bisectors and angle bisectors." The intention of this outcome is for students to be able to describe and demonstrate these constructions using a straight edge and compass. In developing the understanding of these constructions, students are exposed to a variety of methods and tools such as paper folding, Mira, and rulers. I've written about geometric constructions in the past, so I won't get into a discussion of the merits of Euclidean constructions. My concern is that this unit could turn into a series of steps to memorize for a short list of basic geometric constructions that lacks coherence and context. If you really need to construct a heptadecagon using only a straight edge and compass, I'd expect you to look up the steps, not have them memorized. Additionally, in my opinion, the exercises in the student textbook are routine and dull. I think that this is a unit that has a lot of potential for student engagement but could easily become tedious. Dan Meyer gave an inspiring ignite talk titled "Teaching the Boring Bits" at the 2013 CMC-North conference. In this talk, Dan encourages teachers to engage students by creating an intellectual need for new knowledge. Teachers should strive to provide students with a reason to want to know new mathematical skills and methods. A grade 7 teacher that I know thought that incorporating Islamic geometric designs into this unit would give a purpose and context for doing geometric constructions. Another factor in selecting this context was that she has a number students who are recent immigrants from the Middle East in her class. We brainstormed some ideas and developed several activities to infuse into this unit that might help give this outcome some coherence and allow students to be creative and artistic. The teacher started by using a template and pattern from Eric Broug's School of Islamic Geometric Design. Students used the template and followed the instructions to create and colour their designs which were then tessellated in a grid to make a group composition on the bulletin board. Later in the unit, students were challenged to construct eight-pointed stars using geometric constructions without a template (although a template could be used for students that needed additional supports). Creating this design using a straight edge and compass required students to perform the majority of the constructions required by this outcome. Students also had the opportunity to use their creativity to personalize their design and make it unique. A number of students were very interested in creating designs of increasing complexity. They were able to pursue this to apply their geometric skills to create some very impressive designs. Have you used any creative or artistic activities to teach students geometric constructions? If so, I'd appreciate hearing about it!
EL
I've been taking a close look at geometric constructions in the Nova Scotia mathematics curriculum. There is one outcome involving geometric constructions in the NS curriculum. Grade 7 outcome G01 states that students, "will be expected to perform geometric constructions, including: perpendicular line segments, parallel line segments, perpendicular bisectors and angle bisectors." The curriculum guide goes on to define constructions as "performed using a compass and straight edge (without markings) as tools." This is the only outcome that I am aware of that has a focus on the tool being used and not on the mathematical understanding to be achieved. I'm not sure I understand this focus on the tool. Especially such an archaic tool. I can almost hear the students... Student: Why do I have to use a compass and a straight edge to draw this equilateral triangle? Wouldn't it be easier to use a ruler and a protractor? I worked with a bunch of elementary teachers on these compass and straight edge constructions and they found them frustrating and tedious. When we performed the same constructions using patty paper and dynamic geometry software, the teachers found the constructions less confusing, enjoyed them more, and seemed to get a better understanding. So I asked, "why is this outcome so focused on a specific tool?" If we have efficient and accurate modern tools, why do we still teach students to use compass and straight edge? Is it more "elegant and civilized"... like learning Latin even though no one really speaks Latin anymore? Anyway, I love a good Star Wars analogy, so.... In grade 6, students look at transformations of 2-D shapes to create a design. In this outcomes, G04, pattern blocks are used as a tool to explore tesselations and the geometric concepts that result from these designs. The outcome does not talk about the tool being used or tesselations. These discussions are saved for the background of the outcome and its indicators. I recently read an article talking about how students explore tesselations and how their interest can be sparked by creating aesthetically pleasing designs. The author stated that, "tiling provides one of the richest possible studies of geometric concepts as well as a powerful topic for open-ended mathematical exploration, fostering important mathematical practices. For students, mathematical aesthetics can be a guiding force for mathematical inquiry, just as it is for mathematicians." from R. Scott Eberle. ““I Don't Really Know How I Did That!””. Teaching Children Mathematics 21.7 (2015): 402–411. Ultimately, this is what I hope teachers focus on when teaching geometric constructions in grade 7. I'd like to see them work with students on open-ended mathematical explorations of geometric shapes and properties using a compass and straight edge as an entry into this exploration. Memorizing the steps to do geometric constructions should not be the focus of this unit. The focus should be the understanding that comes from working with shapes regardless of the specific tool that is used, exempli gratia compass and straight edge, patty paper, or dynamic geometry software (notice how I used a bit of Latin there?). So why are Euclidean constructions an outcome in the NS mathematics curriculum? That is a good question. Neither the curriculum guide nor the textbook mention the history of compass and straight edge constructions or why students should be practicing them. Here is my hunch... Let's start with some history. Geometry was an integral part of the classical liberal arts education going all the way back to the middle ages and the Qradrivium. Much of the geometry education at this time consisted or reproducing the propositions from Euclid's Elements. Many of the proofs in Euclid's Elements were proven with geometric constructions using a compass and straight edge. Because of this, constructions were an integral part of the curriculum. It was the tool by which Euclid's postulates were both reproduced and proven. Over time, many parts of the classical curriculum have disappeared from modern education. Euclidean constructions however have long had their staunch supporters and remain. Here is a quote from D.E. Smith's book The Teaching of Geometry (1911), "Constructions excite students’ interest, guard against the slovenly figures that so often lead to erroneous conclusions, has a genuine value for the future artisan, and shows that geometry is something besides mere theory." Here is a quote from "Ask Dr. Math" at the Math Forum, that I think best elucidates the reason for constructions in our curriculum. "Certainly learning how to use the tools is useful. Some of the techniques are useful in construction (of buildings, furniture, and so on), though in fact sometimes there are simpler techniques builders use that we forget to teach. But I think the main reason for learning constructions is their close connection to axiomatic logic. If you haven't heard that term, I'm talking about the whole idea of proofs and careful thinking that we often use geometry to teach. Euclid, the Greek mathematician who wrote the geometry text used for centuries, stated many of his theorems in terms of constructions. His axioms are closely related to the tools he used for construction. Just as axioms and postulates let us prove everything with a minimum of assumptions, a compass and straightedge let us construct everything precisely with a minimum of tools. There are no approximations, no guesses. So the skills you need to figure out how to construct, say, a square without a protractor, are closely related to the thinking skills you need to prove theorems about squares." If you have any insight into Euclidean constructions and their place in the mathematics curriculum, I would love to hear your opinions. Nova Scotia Mathematics Curriculum Outcomes Grade 6 G04 - Students will be expected to perform a combination of successive transformations of 2-D shapes to create a design and identify and describe the transformations. Grade 7 G01 - Students will be expected to perform geometric constructions, including: perpendicular line segments, parallel line segments, perpendicular bisectors and angle bisectors. EL
|
Categories
All
|
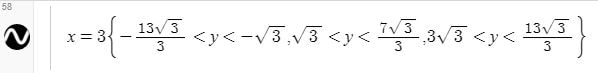

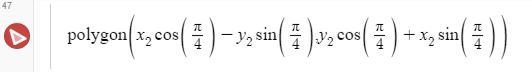



 RSS Feed
RSS Feed