|
Summer is here and I've recently returned from a family vacation that included several lengthy flights. My son just turned eight years old and enjoys flying but can get a bit restless after a few hours on an airplane. Below are a few of the games and activities that we packed to make the time pass enjoyably. These games are best when they are small, lightweight, easy to pack and can be played on the limited space of an airplane tray table (often around 16.5" x 10.5" but there is no standard size). Games are ideally two player but if you're on a larger plane, you might be able to play a three player game. Pencil and Paper GamesGames that can be played with just pencil and paper are ideal for an airplane. We bring a few pencils and a tablet of paper with us for games, sketching or making notes. Here are a few of our favourite pencil and paper games:
Games with Dice, Cards and Counters
Commercial Board Games
Other StuffWhen on a long play ride I also bring snacks, a small LEGO set, and some art supplies to draw or colour with. Do you have suggestions for travel games to play with with your children? I'd love to hear your suggestions. EL
Personal, professional and financial aspects of my life have come to a rare convergence which will allow me to attend the National Council of Teachers of Mathematics (NCTM) Annual conference this April in Washington D.C. This is the first time that I've had the opportunity to attend a conference like this. I've registered, arranged transportation and lodging, double checked my passport and I'm almost ready to go... just a few more steps. Step 1 - Math Convention CarryPacking my pencil case is something I put far too much thought into. This is what I currently have packed.
Step 2 - Pick Out Too Many SessionsOn my first pass through the list of sessions, I just pick out all the sessions that I'd like to attend. It turns out, there are a lot of sessions that I would really like to attend. Now to make some hard choices. Step 3 - Fine Tune My List of Sessions
Step 4 - Listen to Good AdviceSpeaking of advice, I was talking to a colleague yesterday about the NCTM conference. She said to not run from session to session for the whole conference. She said to slow down and talk to people. The networking and discussions between sessions can be very valuable. Returning with a few really good ideas can be better than returning with dozens that get lost in the shuffle. If you have any good advice from a first time NCTM conference attender, please let me know. I'm moving right along and perhaps I'll see you there! EL
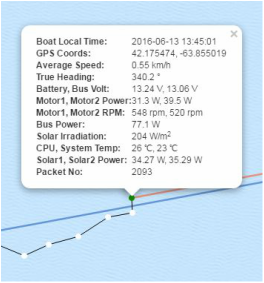
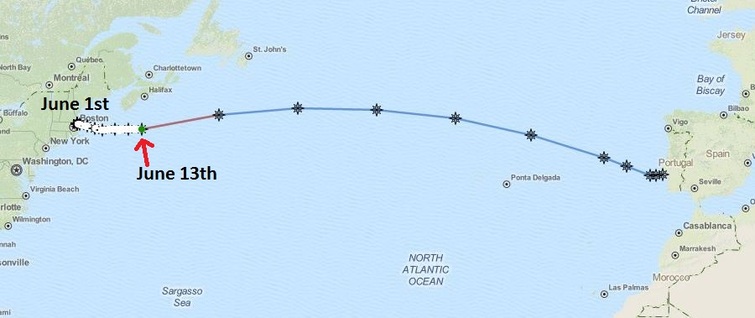
I recently read an article on Wired about the Solar Voyager. A pair of engineers, Isaac Penny and Christopher Sam Soon, designed and built an autonomous, solar powered vessel. On June 1st, 2016 the 18 foot vessel, named Solar Voyager set off on its trans-Atlantic adventure from Gloucester, Massachusetts to Portugal, a journey of more than 4800 kilometres. They are predicting that this trip will take 4 months, assuming that there are no catastrophic events mid-Atlantic. One cool thing about this trip is that the Solar Voyager reports it position and other data online every 15 minutes at http://www.solar-voyager.com/trackatlantic.html. Currently, about two-weeks into its journey, Solar Voyager is just South of Halifax, Nova Scotia where I live. The image below shows how far the Solar Voyager has traveled during its first two weeks. That is 1/8 of the time estimated for the crossing. Based on the information below, do you think that it will reach its destination in 4 months? What factors did you consider when making your estimation? Some factors you might consider are currents, weather, equipment malfunction, obstacles/collisions, wear and tear, etc. There are so many variables at play that it must be very hard to make an accurate estimation. Some Questions/Estimates for Students:
One of the coolest things about this project is that these young engineers "built Solar Voyager in their free time, undertaking this voyage simply for the challenge." How can I commandeer this type of intrinsic motivation for students in math class? What about this project made them want to work so hard "just for the challenge" and not for some extrinsic reward. Was it because they were the ones who selected and designed the task? Did they have just the right skills so that they felt confident that they would be successful? What is something that was relevant to their lives? How did this project captivate their curiosity? Data Points:
Update: Solar Voyager ran into some trouble south of Nova Scotia. It appears it got tangled in some fishing gear and the props and rudders were fouled. After drifting for over a week, the vessel was picked up by HMCS St. John's, a Canadian Navy offshore patrol vessel. EL
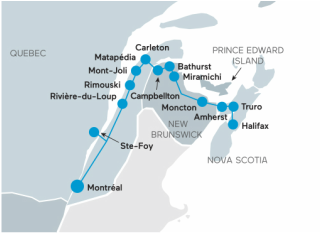
What sort of questions might your students have about this train schedule? How long is this train at the station during a typical week? If this train is at the station in Montréal for a similar amount of time, then how long is each trip from Halifax to Montréal? What is the average speed of this train during its trip? What do you think the schedule looks like that is posted at the station in Montréal? How would this trip via train compare to a trip via car or plane (time, cost, etc.)? EL
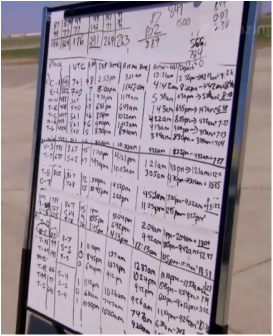
As a math teacher, I always love to see folks doing real math on television. Last week, on The Amazing Race Canada (Season 3, Episode 7), there was a 'tricky' mathematical challenge. Contestants were given a list of Air Canada flights and asked to create a flight plan using Air Canada destinations from around the world. They had to find a set of flights that had a total flight time of 25 hours (or 1500 minutes). They also had to ensure they used "a combination of routes that travel to at least three continents". Calculating the flight time was the first hurdle. Since arrival and departures are listed in local time and the vast majority of these flights crossed multiple time zones, contestants had to use the universal time code for each city to correct for time changes. A number of teams were confused right from the start (there was a lot of fixed mindset talk from the contestants). One team used an 'Express Pass' to skip this challenge while two other teams gave up and took a 2 hour time penalty instead of continuing with the challenge, That is a lot of flights! There are 12 flights listed on the Europe board, 11 flights on the Asia Pacific board and 15 flights on The Americas board. If we use just one flight from each board (so that we visit three continents), there are a total of 1980 combinations (12*11*15=1980). The rules state that we have to visit at least three continents but it doesn't say how many flight to use so we could have a flight plan with more than three flights. If we add one additional flight to make a flight plan with four flights, now we have 69300 possible flight plans (12*11*15*35=69300... one flight from each board and any one of the remaining 35 flights). That is a LOT of trial and error. The two solutions shown on the episode contained 4 flights. Are there any 3 flight plans that would work? Here is what I did.
First I got some screen captures of the flight boards so I could read all the flight times. Then I put them all into an Excel spreadsheet to calculate the flight times in minutes. Next I played with Excel for about an hour to try to find an efficient way to calculate all the combinations of flights that I wanted to try and then gave up. Instead, I created a quick program in Python to calculate all the possible sets with just three flight plans. This turned out to be much easier than using Excel (just 8 lines of code). AList=[924,731,635,1016,802,640,831,744,767,658,772] BList=[566,453,488,408,447,433,424,461,457,490,522,514] CList=[343,87,99,192,325,616,324,363,650,335,337,77,183,640,316] for i in AList: for j in BList: for k in CList: if i+j+k==1500: print 'Eureka!',i,j,k Now, assuming that I calculated the correct flight times in my Excel spreadsheet, this gave me three possible solutions: 1- AC025 Vancouver to Shanghai, AC824 Toronto to Amsterdam, AC541 Toronto to Seattle 731 + 453 + 361 = 1500 minutes 2- AC084 Toronto to Tel Aviv, AC898 Edmonton to London, AC962 Toronto to Bogota 635 + 522 + 343 = 1500 minutes 3- AC056 Toronto to Dubai, AC1904 Toronto to Edinburgh, AC1973 Halifax to Calgary 767 + 408 +325 = 1500 minutes The two solutions that were shown on the episode using four flights are below: AC480 Toronto to Montreal, AC918 Toronto to Miamai, AC882 Toronto to Copenhagen, AC007 Vancouver to Hong Kong 77 + 192 + 447 + 784 = 1500 minutes AC230 Vancouver to Calgary, AC541 Vancouver to Seattle, AC1910 Montreal to Nice, AC009 Calgary to Tokyo 87 + 316 + 457 + 640 = 1500 minutes
There was a nice article posted online that interviewed the Air Canada captain that handed out the clue cards for the challenge. He mentions the factors that he said made this such a challenging competition.
EL |
Categories
All
|
||||||||||||||||||||||||||||||||||||||||||||||||||

















 RSS Feed
RSS Feed