|
When I first started teaching, reviewing for a test meant one thing. I would stand at the front of the room and reteach each unit, section by section. I would carefully annotate important points and questions that would likely be on the assessment. After reteaching the material, I would hand out a large packet of questions for students to work on. I found that while this helped some students, many students were either bored or confused. If they didn't understand it the first time, hearing me teach it again the same way probably wasn't helping. If they already understood the material then listening to me teach it again was not helping them learn it any better. I recently ran across a couple of blog posts from MathMedic reminding me of why I do things differently now.
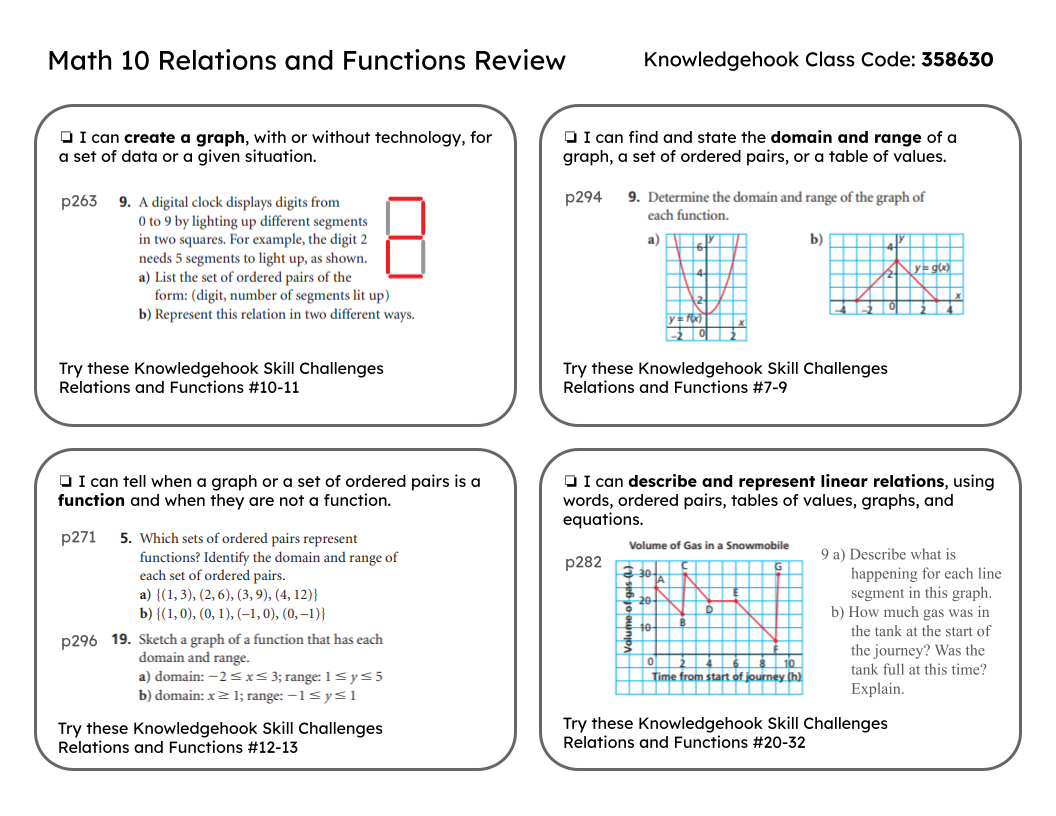
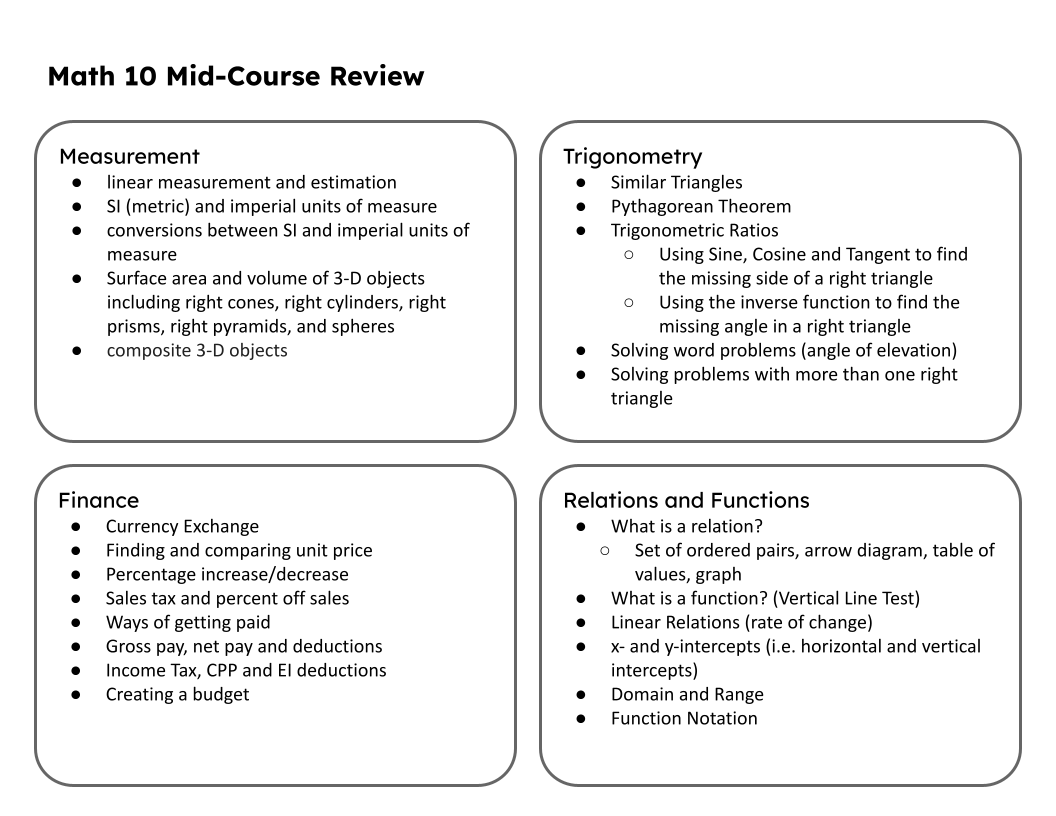
My Mathematics 10 class recently reviewed for a unit test and now we're reviewing for a cumulative assessment on the first half of the course. I typically start with some individual self-assessment where students can review outcomes and identify areas where they need additional practice or review. Next I give students a variety of ways to practice the areas they identified for themselves. Then I like to finish with a (hopefully) fun review game to wrap things ups. Student Self-AssessmentFor our Relations and Functions assessment review, I started with an overview of the outcomes for the unit so students could identify areas where they needed additional support.
Another way we reviewed was to have students in small groups at vertical whiteboards make a list of the most important topics, formula and skills from each unit. This ends up being a study sheet. After groups complete it, they share with the class to see if any groups has something that would benefit everyone. I then collosidated all of these into one class sheet that could be shared on our Google classroom. Individualized ReviewAfter this, I gave them some options to reivew and practice the areas they identified as a challenge. Sometimes this looks like the day in class we practiced domain and range.
Students that want to hear the topic being taught again have lots of options online. There are tons of YouTube channels full of teachers providing lessons on specific topics. I recently found out that a teacher from my school has his own YouTube channel with videos from our curriculum (way to go Mr. Boudreau!). There are also videos on the Nova Scotia Homework Hub, the CEMC Waterloo Courseware site, and many others. Group ReviewTo finish off, I like to play a class game where students work together to study and have some fun while doing it. A game like math basketball is a favourite in my class. We've also done self checking activities like Add 'Em Up or a Scavenger Hunt. Today for the last class of the semester before our assessment, we had a "math market" activity. Students can "buy" questions of different difficulty levels and topics from the market and "sell" solutions back for a profit.
Hopefully students learn lots and find class challenging. I still have lots to learn about teaching and am really trying new things out with my class this year. Let me know if you have a favourite review activity I should know about.
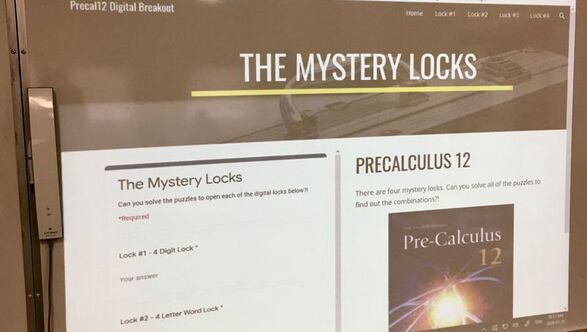
I recently had the opportunity to try out a digital breakout with a Precalculus 12 math class. The classroom teacher and I wanted to create an opportunity for students to have some interleaved practice as a cumulative review for the course. We liked the idea of a breakout game but we wanted to make sure that all of the students got a chance to do a wide variety of problems. Our solution was to do a digital breakout in small groups of 2-3 students. This was the first time that I had created a digital breakout game so I went hunting online for some examples that might spark some ideas. I found Tom Mullaney's (@TomEMullaney) Digital Breakout template page to be very helpful in figuring out what I was going to do. It gave me lots of ideas and inspiration. I also found I found a post from Meagan Kelly (@meagan_e_kelly) showing an example of a math digital breakout that I was just what I was looking to do. I learned how to create a google site and conquered a number of new technical challenges. While creating the site took some effort, the classroom setup was easy and there were no materials required. I thought the breakout went well. The students were very engaged and they reviewed lots of different concepts from throughout the year. They liked working in groups and having a variety of different types of puzzles to solve. Many students were consulting their notes and examples from the textbook to find solution strategies. They were also using online tools like https://www.desmos.com/ to help them graph and visualize mathematical relationships. All the problems were self-checking. If the combination for a lock didn't work, they knew that they had made a mistake and had to work together to find and solve it. They also all got to work at their own pace. To add a bit of additional flair, we added a final physical lock and box for students to unlock with a small treat inside. If you'd like to give this breakout a try, check it out. The link is: bit.ly/PC12Breakout. EL
Activities that let students get immediate feedback on how their are doing are extremely beneficial. Activities that allow students to self-check their own work allow for this immediate feedback and correction. These types of activities can allow the teacher to focus their time with students who are having conceptual misunderstandings and not get bogged down helping students find and correct computational errors. While students are engaged in self-checking activities, the teacher can also be working with small groups of students on mini-lessons or conversations/conferences. Below are a few of my favourite activities and routines that allow for students to check their own work: Team Post-Its - I recently saw this activity described in a post by Julie Morgan. This activity is very easy to set up and does not require much front loaded time to create. The teacher posts a list of questions for small groups of students to work on. These might even be questions from the textbook. Each group solves the question, writes their answer on a sticky note and posts it on the whiteboard. As other groups complete the questions, they can compare their answers to those from other groups to see if they agree. If they don't agree, they double check their work. I would suggest that each group of students starts with a different question. Add ‘Em Up - In this activity, students do a set of problems, either on their own or as a group. These problems typically have numerical answers. The answers to the set of problems are added up and compared to the sum provided. If the sum is not the same, then the student knows that one or more of the problems in the set was done incorrectly and works to find the error. I first saw this activity described in a blog post from Kate Nowak. I later saw a blog post from Amy Gruen describing a simple and quick way to do this same activity that I used occasionally. There are many descriptions of how to organize this activity including one in a detailed blog post from Sara VanDerWerf. Row Game - I also first saw this activity described in a blog post from Kate Nowak. Typically, a row game is a worksheet of problems organized in two columns. The worksheet is completed by a pair of students, one doing the problems in column A and the other doing the problems in column B. The problems in each row have the same answer so if the students' answers don't match, they can work together to check their solutions to find the error. To make row games a bit easier to create, you can create an additional column with the sum of the solutions from column A and B (similar to the Add 'Em Up activity from above). This allows you to use any two problems and not have to create two problems with the same solution. Kate Nowak has a shared google folder with a large selection of crowd-sourced row games. Added 03Oct017 - I recently saw a great idea from Heidi Neufeld. She asked students who finished quickly to make a new row for the row game and create two different problems with the same answer.
Mathematical Circuit Training / Around the World / Star Chain / Question Stack - There are lots of different names for and variations of this activity. The essential part is that there is a series of problems and the answer for each problem leads you to the next question to ask. The answer to the final question leads you back to the starting question. This activity can be organized as a simple worksheet, a stack of cards to turn over, a set of cards to chain together or questions posted on signs around the classroom or hallway. If you make a mistake, you won't be able to find the next question and you know to try again. This can be done individually or in small groups.
Added 26Sep2017 - Thanks Alicia! Invisible Ink - The description of this activity is from a blog post from David Petro. Students solve a set of problems on a card. When ready, they can check their solutions using an answer card. This card has the correct answers written with "invisible" ink that can only be seen by shining a small UV light on it. Once the student has solve the questions correctly, they move on to the next card containing more complex questions. David says, "Students really seem to like this style of activity as they feel empowered to move from card to card when they are ready and the added feature of checking the answers with the UV pen gives a sense of novelty." If you know of any other self-checking activities that I've missed, please let me know and I'll add them here. EL
High school exams in Nova Scotia (grade 10-12) typically run in the second to last week in June. This is the time that grade 9 students are writing some exams as well. The week prior to exams is often set aside by teachers for a cumulative review. This is a time to revisit the curriculum outcomes, consolidate learning and make final connections. What teachers do with this review time can vary greatly from class to class. Many teachers create a booklet of review questions that cover the main topics from the course. This can be a helpful resource for some students but not all that engaging. Here are some additional ideas for reviewing outcomes that might increase student engagement and allow for some differentiation.
No matter how you decide to review for the exam, by the time you get to exams, "the hay is in the barn". Here is a note from Alberta Education... "The best way to prepare students for writing the achievement test is to teach the curriculum well and to ensure that students know what is expected. Many of the skills and attitudes that support test writing are, in fact, good skills and strategies for approaching all kinds of learning tasks." EL
|
Categories
All
|
||||||||||||||||||||||







 RSS Feed
RSS Feed