|
Yesterday I gave a presentation on self-checking math activities for the 2023 NCTM Virtual Conference. I find presenting at conferences valuable because it makes me reflect on my work and think deeply about why I'm selecting or creating certain activities for the classroom. I thought I was finished with my presentation when I saw a variation of a loop card activity that I decided to give a try. Loop cards make for a great self-checking math activity. In a "loop card" activity, the rectangular cards each have two values or expression on them, much like a domino. Students evaluate the expression on the right of side of the card and find a different card whole value on the left side is equivalent. These cards are then joined together (for example, x+3=7 on the right side of one card would join with x = 4 on the left side of another card). Students continue this way until a loop is created with the cards. For a nice example of loop cards, check out Don Steward's post at https://donsteward.blogspot.com/2015/02/loop-cards.html. The variation on this activity that I saw was NRICH's Doughnut Percents activity. In this activity, four students work as a team. Each student is given four cards and tries to make a small loop (for a total of 16 cards). They will typically not have the correct cards and need to trade cards with other members of the group. When complete, there will be four, four-cards loops created, one for each student. The twist with this activity is that the students have to do this quietly. They can just grab cards from other members of the group, but wait for the other student to give them a card that they need. It is very difficult for students to work together silently. I was inspired by this activity to give it a try with other classes. I created a "Derivative Donuts" activity and gave it a try with a Calculus class to review power, product, quotient and chain rules for derivatives. The google slides file can be found here: https://docs.google.com/presentation/d/1lMrJhNWY3jPCqlZrui8EBPe5YeCUdLxt3-akhkGwPxU/edit?usp=sharing. The cards are organized by loop in this file... with a larger group, I would mix the cards up and then have students cut them out... many hands make light work. I used the percent activity above to teach students the rules for the activity using content that they were confident with. Then I gave them the derivative activity which they found challenging. I thought that this activity was a nice change from a typical card sort or question stack type of activity. I like that students worked together as a team to try to create the loops. Because students weren't talking, one student wasn't able to dominate the team and take over the process. Each students had to participate for the group to be successful. The next time I try this activity, I'm going to try having teams of three students with five questions each. I think groups of three might be easier to form small groups (although I'll need more sets of cards). I also recently saw NRICH's Simplifying Doughnut activity which I'm looking forward to try with students. EL
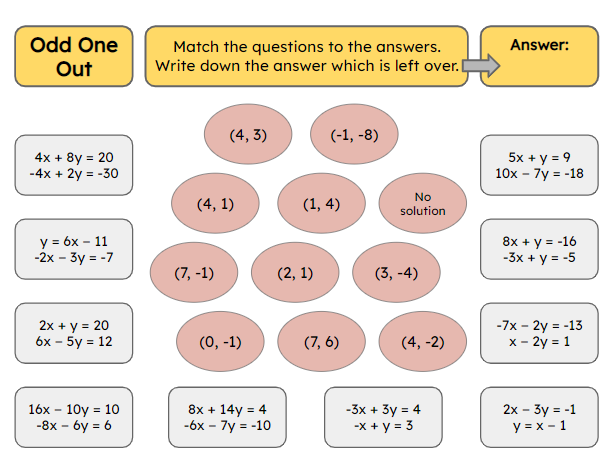
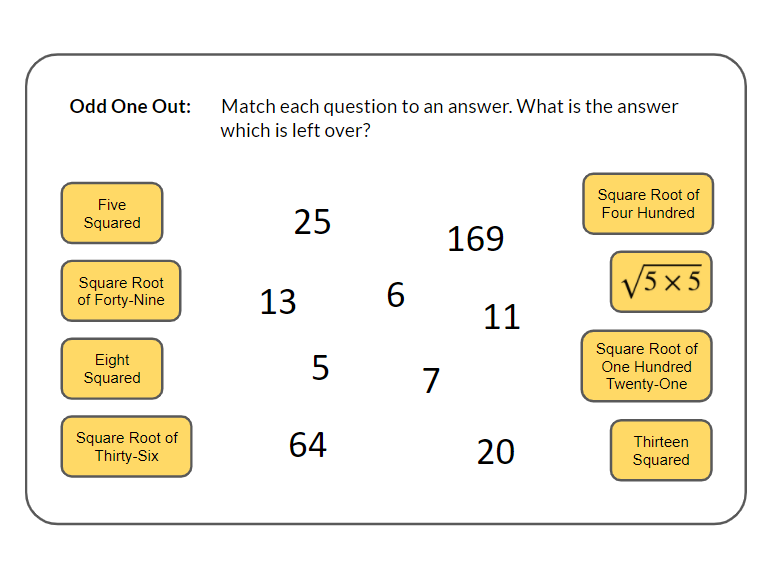
Self-checking activities allow students to have immediate feedback on how they are doing. When these activities are completed in small groups, it gives students an opportunity for meaningful mathematics discussions. Students determine if they have the correct answers and if they don't, they can work together to determine where their mistake is. This allows the teacher to focus on groups that have misconceptions or misunderstandings as students will often find and correct their own computational errors. A self-checking activity that I've recently been using is called "Odd One Out." I was inspired by a couple of activities that I found on TES. The first example was a page showing a number of expressions to evaluate using the order of operations. In the center of the page was a bank of possible solutions. There were 15 expressions and 16 solutions. The solution left over when all the expressions were evaluated was the "odd one out." The other example showed four sets of five linear equations to solve. All of the equations in each set had the same solution except for one. The goal was to identify the equation with the "odd one out" solution. Below are two "Odd One Out" problem sets that I created. The first one is to practice solving systems of equations and the second is to practice solving precentage problems. You could also use this activity as a quick warm-up with fewer numbers. Jo Morgan (@mathsjem) shared an activity from MathsPad on her Math Gems #74 that had a sets of 9 radicals (surds): 4 simplified, 4 unsimplified and 1 odd one out. You could also use the same format as above with fewer questions. A couple of short examples below. Craig Barton (@mrbartonmaths) highlighted Odd One Out activities in a "Maths Resource of the Week" in late 2016. He describes a few different varieties of this activity and also points to a variety of different examples of this resource. Have you used an odd one out activity with your students? How did you use it? EL
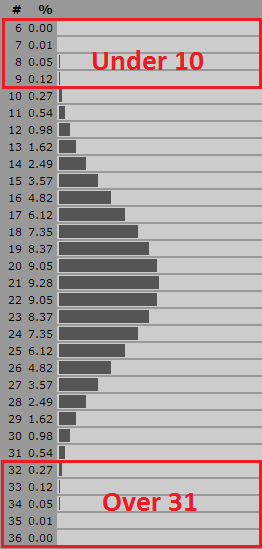
My son and I recently spent a lovely fall afternoon exploring the carnival games and amusement rides at a local fair. My son is quite adventurous when it comes to amusement park rides and is eager to try just about any ride that he meets the height requirement for. While we were walking through the midway, I spotted a carnival game called "Roll Down" that appeared to have a bit of mathematics involved. The object of this "game of skill" is to roll six balls down and inclined ramp to land in one of six numbered bins. If the sum of the six rolls is under 10 or over 31, you win. Is this game worth the $5 price to play? What are my chances of winning? Should I go for under 10 or over 31? Is this just a carnival scam or is there some skill involved? The bins are just wide enough for a ball to fit so it is very difficult to aim a ball with accuracy. You also have to question if the balls roll straight and if the board is smooth and level. Lets just assume that the balls fall into a random bin (you could then play an equivalent game at home by rolling 6, six-sided dice). With six balls, the smallest sum possible is 6 (all 1's) and the largest is 36 (all 6's). How many ways are there to get each possible value? There are only 31 possible sums (6-36) that you can score. To roll a sum of under 10, you can score 6, 7, 8 or 9. To roll a sum of over 31, you can score 32, 33, 34, 35, or 36. At first glance, it looks like you have a 9/31 chance of winning but this is not correct.
This reminds me of a bet in the casino game craps that looks good, but on further inspection is really bad. The field bet is a bet on the sum of the next roll of two six-sided dice. If the sum of the two dice is 2, 3, 4, 9, 10, 11 or 12 you win. If the sum is 5, 6, 7 or 8 then you lose. It has the illusion that there are more ways to win than lose, but you are much more likely to roll one of the losing numbers. With practice at Roll Down, you might be able to achieve better than the random results that I detailed above. Instead of this practice, I decided to spend my $5 at the concession stand to buy a hand-battered, deep fried corn dog. A midway concession stand can also be considered a bit of a gamble, but in this case it was a delicious win! EL
Here are a few questions that I thought about:
Below are some additional photos: Given the list of lego bricks, you could ask students a number of additional questions:
The Discovery Centre is currently working on a project to build Canada's largest Lego mosaic wall. The wall will be installed at the Discovery Centre's new location when it moves. Nova Scotia Mathematics Curriculum Outcomes Mathematics 7 - N07 Students will be expected to compare, order, and position positive fractions, positive decimals (to thousandths), and whole numbers by using benchmarks, place value, and equivalent fractions and/or decimals. Mathematics 8 - N03 Students will be expected to demonstrate an understanding of and solve problems involving percents greater than or equal to 0%. Mathematics 8 - N04 Students will be expected to demonstrate an understanding of ratio and rate. Mathematics 9 - N03 Students will be expected to demonstrate an understanding of rational numbers by comparing and ordering rational numbers and solving problems that involve arithmetic operations on rational numbers. Mathematics at Work 11 - G02 Students will be expected to solve problems that involve scale. EL
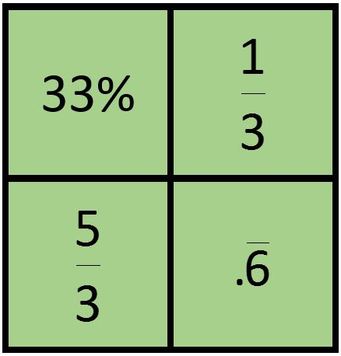
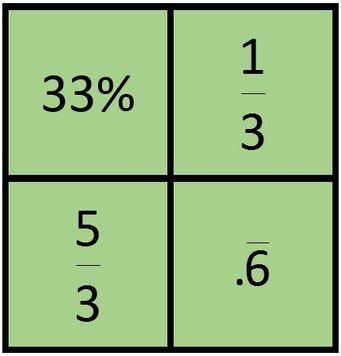
I've mentioned in the past that I think WODB questions are a great way to begin a lesson and engage students in a mathematical discussions. Below is one such question I created for grade 7 students. Most are working in or have recently finished Unit 3 on Fractions, Decimals and Percents. The question below might be a good review now that students have the language and vocabulary to debate which one doesn't belong. Here are some suggestions and why each number might not belong: Top Left: It is the only percentage and it is the only number with a tens place. It is also the only number without a vinculum. This is also the only number that is not an exact multiple of 1/3. 33% would be 33/100 and so is just a bit less than 1/3. If all the numbers were written as decimals, this would be the only terminating decimal. Top Right: It is the only number that would be a unit fraction when written as a fraction Bottom Left: It is the only value "greater than one". 33 is great than one but since it is a percentage, it represents 33/100. Bottom Right: This is the only even number and also the only term without the digit 3 in it. It is also the only number written as a decimal and the only box with just one digit in it. If your students are not used to participating in this type of discussion, you might scaffold it by first having students brainstorm and list the vocabulary and math terminology that might be used in the coming conversation. This might be especially helpful in a late French Immersion classroom where all students might not be familiar with the correct vocabulary. Having it listed on the board might help students feel more confidence in joining in the conversation. For the fractions, decimals and percent WODB above here is a list of vocabulary students might come up with: unit fraction, improper fraction, mixed number, percent, terminating decimal, non-terminating decimal, even and odd. A special thanks to Matt Murphy (@Lemurph42) for the following translation of the above post! Lequel n’appartient pas? Les Fractions, Décimaux et Pourcentages.J’ai déjà dit que je trouve les questions de WODB font un bon départ pour engager les élèves en discussions mathématiques. Ci-dessous il y a une telle question que j’ai créé pour les élèves de 7e année. La plupart de nos classes ont déjà complété chapitre 3 (fractions, décimaux et pourcentages), ou le finiront bientôt. L’exemple suivant pourrait être une bonne révision maintenant que les élèves ont le vocabulaire nécessaire pour s’engager en débat. Voici les arguments pour chaque choix : Gauche supérieure: c’est la seule pourcentage et c’est le seul nombre avec un chiffre à la position des dixaines. C’est aussi le seul nombre qui n’a pas une surlignéation. Ce n’est pas un multiple de 1/3 (33 % sera 33/100, un peu plus petit que 1/3). Si tous les nombre seront écrit comme décimal, c’est le seul qui termine. Droite supérieur: c’est le seul qui est une fraction unitaire. Gauche inférieur: le seul nombre qui est « plus grand qu’une ». C’est vrai que 33 est plus grand qu’une, mais puisque c’est une pourcentage, la valeur est 33/100 en réalité. Droite inférieure: c’est le seul nombre paire et il ne contient pas le chiffre 3. C’est le seule nombre en forme décimal et le seul qui ne contient qu’un chiffre. Si vos élèves ne sont pas habitués à tel sorte de discussions, vous pouvez utiliser l’échafaudage. D’abord, demandez aux élèves de faire un remue-ménginges du vocabulaire mathématique qui pourrait être utile dans la conversation. Ceci pourrait être utile dans une classe d’immersion tardive dont les élèves ne seront pas familiers avec tous les mots de vocabulaire. La confiance des élèves augmentera avec une liste mots disponible au tableau, faisant qu’ils seront plus capables à participer. Pour la WODB des fractions, décimaux et pourcentages en haut, voici quelques mots de vocabulaire que, peut-être, vos élèves fourniront: fraction impropre, nombre mixte, pourcentage, décimal terminé, décimal illimité, paire, impaire Nova Scotia Mathematics Curriculum Outcomes Grade 7 N07 - Students will be expected to compare, order, and position positive fractions, positive decimals (to thousandths), and whole numbers by using benchmarks, place value, and equivalent fractions and/or decimals. Grade 7 N03 - Students will be expected to solve problems involving percents from 1% to 100% (limited to whole numbers). EL
|
Categories
All
|













 RSS Feed
RSS Feed