|
Have you ever had a student look at you like you're talking in a foreign language during a math lesson? It happens. Sometimes there are gaps in students' prior knowledge. Sometimes students need more time to process a new concept in order to construct and develop their understanding. Sometimes I haven't explained something clearly and I need to think of a new approach to tackle this topic. When I encounter those blank stares, I think, "That's Numberwang." Numberwang is a skit from That Mitchell and Webb Look, a British sketch comedy show from 2006. If you've never seen it, take a two minutes to watch a video of this skit. The premise of the skit is that while the presenter and contestants seem to understand the rules perfectly, they are completely inscrutable to the viewer. We're left scratching our heads in confusion just like our students sometimes do in class. Delve!So what do you do when you sense that students in your class are not getting it? I suggest that you invest some time to uncover your students' thinking. As Guildenstern implores in Tom Stoppard's play Rosencrantz and Guildenstern Are Dead, "Delve. Probe the background, establish the situation." Take the opportunity check in with students to determine their level of understanding. Here are some strategies you might use:
Reflect and RespondOnce you have a better picture of the misunderstandings and misconceptions that may be present in your class, you can plan your next steps. Was there really a misunderstanding or did you make assumptions about prior knowledge that weren't true? Were just a few students struggling or was it a commonly held misconception? Tracy Zager, in her book Becoming the Math Teacher You Wish You'd Had, writes, "If just a few students were confused, she could work with them individually. If there was a really interesting mistake, or patterns among the misunderstandings she saw, she could use those examples as her next teaching opportunity." When I see those "Numberwang" looks I am reminded that even a well planned lesson can sometimes miss the mark. Reflecting on how a lesson went and how I can improve it helps me refine my teaching practice and be more responsive to students' needs. Don't let those "Numberwang" moments go by ignored. Matt Larson, in his August NCTM president's message, wrote "Making mistakes, getting feedback from our colleagues, and making iterative improvement are part of the natural process of continual growth. We should never forget that perseverance isn't just for students—perseverance also applies to us as professionals." EL
 https://www.ted.com/ https://www.ted.com/ I am trying to be purposeful and organized in taking the "Calls to Action" from the recent NCTM conference in San Francisco. I am going to play with "Deleting the Texbook" over my next few blog posts (watch Meyer's most recent NCTM presentation here for elaboration). Since I attended my first conference about 7 years ago, I have been heavily influenced by the work of Dan Meyer. His Ted Talk "Math Class Needs a Makeover" really changed the way I thought about teaching math.  I want to share something I did with first as a math coach with a class of grade 3 students and then as a presentation for teachers at the Nova Scotia MTA conference a few year back. I feel like I have been taking this particular "Call to Action" for many years now; I am excited about the evolution of this thinking and I wanted to show how I started with this work. The students in this class were a few weeks out from writing a provincial math assessment. The classroom teacher wanted to do some questions from the practice booklet. This was the original question:  Instead of posing the question as is, I took out as much information as possible while keeping the math I wanted the students to learn in mind. The students needed to get curious before I hit them with the math. All staff at schools need to wear an ID badge and laynard (wait for it...it will make sense in a moment). Lots of people keep keys, change, notes, etc in the plastic badge holder. Instead of asking the above question, I announced to the class that I had some change in my ID holder (I put the correct amount in and shook it for dramatic affect!). Their job was to figure out how much money I had. They were a little confused at first, so I prompted them; I told them they could ask me questions about the coins. I gave them a few minutes to think, then to confer with a partner before I took questions from the class. I recorded and answered their questions. Here are the questions they came up with along with my answers in brackets:
Each time I took a question, I asked students "Why do you want to know that?" or "How will that information help you solve the problem?" Once they had all the information they felt they needed, they set off to solve the problem. They basically constructed the original question on their own. And because they had a part in building it, they really understood the context of the problem and had ideas of how they might solve it. When they were confident that they had the solution, I let them empty my ID badge and count the coins. That is much more satisfying than just giving the correct answer. Students got to prove that they were right, rather than the teacher being in charge of all the answers. I often hear from teachers that their students don't understand word problems and that it's not the math, it's reading comprehension. I see this strategy of building a question with the class as a way to help them get inside the problem before they start. Another reason I like this strategy so much is that I was able to create it by modifying a resource (practice booklet) that I already had. We can get bogged down trying to find appropriate resources for students at appropriate levels. By using a resource I already had, taking out parts, and layering them back in as needed I was able to differentiate on the fly. No tiered lesson plan, no separate handouts. It was one problem that we worked together as a class to first build, then solve. The Most Interesting Question I Almost Overlooked"What kind of coffee do you drink?
I didn't understand where the student was going with the question but I asked the usual questions of him: "How will that help you solve the problem?" and "Why do you want to know?" The student thought I probably kept my coffee money in my ID badge. If he knew the coffee I drank, he would have the problem solved.** Based on his question, we created a series of extension questions to keep the problem solving going. **All Canadians know the price of a medium double double. :P KZ I get so excited when my kids tell me stories of what is happening in their math classes. This is a favourite. My youngest son (age 7, grade 2) began his story as soon as I picked him up from school. "Mommy, did you know that if you wanted to buy, let's say some....fabric, you couldn't just like go the fabric store and say 'I'll have 20 pencils of fabric'" I was curious where this was heading; being a mathematics consultant, I knew what grade 2's were working on at this time of year (measurement). I didn't want to steal his thunder, so I just went with it. "Really, Michael?" I turned into teacher mode: "Can you tell me some more about that?" He went on to explain in great detail and with loads of enthusiasm about all the trouble he would run into if he wanted to measure fabric with random objects. He actually had a lot of fun naming all of the things that would be silly to use to measure fabric. He went on for a while and wrapped up the conversation telling me there was this "thing" called a "centimeter" that we could all use and understand. You would swear he discovered the metric system himself; he took such ownership of the concept. Keep in mind, I can't think of a time he has ever been in a fabric store (I am not the crafty type) and I am almost certain that before this math lesson, he would never have used the word fabric (cloth or material, maybe?). So he had no previous experience with the concept but he was still engaged? Yes. When I was at Dan Meyer's NCTM presentation (Beyond Relevance & Real World: Stronger Strategies for Student Engagement) last week, I couldn't help but think of this story from my son. I can imagine the kind of "teacher moves" my son's teacher used. She is a natural story teller, her enthusiasm is contagious and she loves to laugh. I can imagine her telling a story to the class, strategically leaving out important parts, having them experience her fabric store dilemma for themselves and brainstorming ideas with the class on how they can fix this problem! Even if he didn't really discover the metric system, he certainly thought he did. And his teacher created those conditions. And I think that's pretty cool. KZ |
Categories
All
|

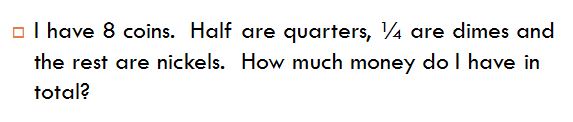

 RSS Feed
RSS Feed