|
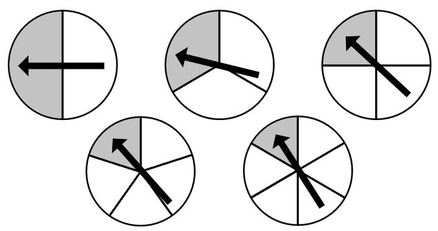
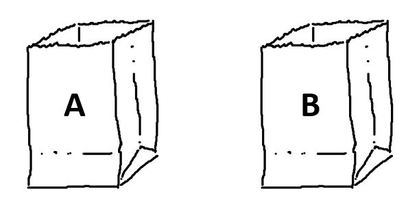
Open middle questions make for great classroom discussions. These are problems that have a closed beginning and end (i.e. an uncomplicated initial question and a single final answer) but an open middle where students can explore different paths and strategies to get to the solutions. Openmiddle.com is a great resource to find these types of questions. Below are a pair of open middle style problems I created for some of the probability outcomes in the NS Mathematics curriculum. Problem #1 - The Spinners Problem Directions: Select three of the spinners below (you may pick more than one of each) such that the total number of sectors in all three spinners totals 10. Select spinners so that the probability of all three spinners landing in the shaded sector is the smallest (or largest). Hint: There are only 4 different ways to select 3 spinners whose sectors add up to 10. In other words, how many ways can you a make a expression with 3 terms that add up to 10 using the numbers 2, 3, 4, 5 or 6. Solution: The four different options for selecting spinners are below. Option 1 yields the greatest probability and option 4 yields the least probability. 1) The greatest probability: 1/2 * 1/2 * 1/6 = 1/24 2) 1/2 * 1/3 * 1/5 = 1/30 3) 1/4 * 1/4 * 1/2 = 1/32 4) The least probability: 1/3 * 1/3 * 1/4 = 1/36 Extension: How would this problem change if you removed the restriction of exactly three spinners? If you could create as many spinners as you wanted such that the sectors totaled to 10 (e.g. 1 spinner with 10 sectors or 5 spinners with 2 sectors, etc.) what would the greatest probability be? 1) The greatest probability: 1/10 = 1/10 2) 1/2 * 1/2 * 1/2 * 1/2 * 1/2 = 1/32 3) 1/5 * 1/5 = 1/25 Problem #2 - The Marbles Problem Directions: "There are _____ red marbles and _____ blue marbles in Bag A. There are _____ red marbles and _____ green marbles in Bag B. " Place a different whole number from 1 to 9 in each blank to make the probability of drawing a red marble from either bag A or B the same. How many different ways can you find to do this? Hint: How can you have a different number of red marbles in each bag but the same probability of selecting a red marble? Solutions: The are 40 different solutions! I first found 5 solutions and then realized that if you just flip the number of red marbles with the other colour, you get another 5 solutions. Then I realized that if you swap the bags, you double the solutions again. I made a Python program to check my work and realized that I had still missed a few and added them in. 1) Bag A: 1 red and 2 blue; Bag B: 3 red and 6 green For each solution below, the following 3 rearrangements are possible. 1B) Bag A: 2 red and 1 blue; Bag B: 6 red and 3 green 1C) Bag A: 3 red and 6 blue; Bag B: 1 red and 2 green 1D) Bag A: 6 red and 3 blue; Bag B: 2 red and 1 green 2) Bag A: 1 red and 2 blue; Bag B: 4 red and 8 green 3) Bag A: 1 red and 3 blue; Bag B: 2 red and 6 green 4) Bag A: 1 red and 4 blue; Bag B: 2 red and 8 green 5) Bag A: 2 red and 3 blue; Bag B: 4 red and 6 green 6) Bag A: 2 red and 3 blue; Bag B: 6 red and 9 green 7) Bag A: 2 red and 4 blue; Bag B: 3 red and 6 green 8) Bag A: 2 red and 6 blue; Bag B: 3 red and 9 green 9) Bag A: 3 red and 4 blue; Bag B: 6 red and 8 green 10) Bag A: 3 red and 6 blue; Bag B: 4 red and 8 green If you want to make this problem a bit easier, just use the numbers from 1 to 6. This gives a total of 16 solutions. These would be 1, 3, 5, and 7 from above plus the 3 additional re-arrangements of each. Extension: Make the number of green marbles a 2 digit number. Nova Scotia Mathematics Curriculum Outcomes Mathematics 7 - SP06 Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. Mathematics 8 - SP02 Students will be expected to solve problems involving the probability of independent events. Mathematics 10 Essentials - G1 Express probabilities of simple events as the number of favourable outcomes divided by the total number of outcomes Mathematics 12 - P03 Solve problems that involve the probability of two events. EL
Comments are closed.
|
Categories
All
|
 RSS Feed
RSS Feed