|
I recently discovered that the way that prices are shown on rate signs for motor vehicle fuel varies quite a bit. Some display the current price in dollars, some in cents and some, confusingly, show both dollars and cents. None of the signs that I found actually showed the units being displayed ($, ¢, L, gal., etc). I decided that it would be a good topic for a Which One Doesn't Belong discussion that would focus in on decimals, place value and fractions as well as currency and volume measurement. Here are some suggestions why each image might not belong as well as some additional information for discussion: Top Left: This is the only fuel price sign with both a decimal and a fraction. It is from a Costco in Oregon. The price is $2.29 and 9/10¢ per gallon. Both dollars and cents are used in this price. If you assumed that the entire price was listed in dollars, then $2.29 and $9/10 would actually give a price of $2.29 + $0.9 = $3.19. Top Right: This is the only fuel price sign with just one decimal. It is from a Shell station in Halifax, NS and is in Canadian cents per litre. In Nova Scotia, the price often doesn't end with the standard 9/10¢ since the price is regulated by the Nova Scotia Utility and Review Board and only changes once per week. Bottom Left: This is the only fuel price sign with two decimals. It is from an Atlantic Superstore gas station in Dartmouth, NS. Similar to the sign above it (top left), it displays a price of $1.00 and 0.5¢ per litre. While probably not confusing to the average motorist, I find the use of two decimals to be mathematically troubling. Why not just list the price as $1.005? Bottom Right: This is the only fuel price sign with no decimals. It is from a 76 gas station in Oregon and is in US cents per gallon. It is interesting to note that Oregon and New Jersey are the only two US states with laws prohibiting self serve at gas stations. This sign mentions "Mini Serve" to note that an attendant operates the pumps but does not provide any of the other services you'd expect with full service.
Nova Scotia Mathematics Curriculum Outcomes Grade 5 N09 - Students will be expected to relate decimals to fractions and fractions to decimals (to thousandths). Grade 5 N10 - Students will be expected to compare and order decimals (to thousandths) by using benchmarks, place value, and equivalent decimals. Grade 6 N01 - Students will be expected to demonstrate an understanding of place value for numbers greater than one million and less than one-thousandth. Grade 7 N07 - Students will be expected to compare, order, and position positive fractions, positive decimals (to thousandths), and whole numbers by using benchmarks, place value, and equivalent fractions and/or decimals. EL
I created the above WODB question for a group of elementary teachers. I spent quite a bit of time creating and revising it (you can see my drafts below). Making a good WODB problem takes a bit of practice I've found. I'm a bit embarrassed about how poorly designed (and sometimes goofy) some of my earlier attempts were. Here are some suggestions why each image might not belong: Top Left: It is the only shape with more than one interior shape (a triangle and two trapezoids). It is the only shape that is not composed of congruent shapes. The only shape without rotational symmetry. Top Right: It is the only shape with 4 interior shapes. It is the only shape whose interior shapes are all similar to its exterior shape. It is the only shape with a single angle measure (60 degrees). Bottom Left: It is the only shape with right angles in it. It is the only triangle that is point down (it tips over). Bottom Right: It is the only shape which includes concave shapes. It is the only shape with interior reflex angles in it. The only shape without reflective symmetry. Updated 9/2/2016 - Added some additional suggestions regarding symmetry from Jennifer Bruce. I've been working with Van Hiele's levels of geometric thinking lately and how it relates to the geometry outcomes in the NS Mathematics curriculum. This got me thinking about how a student's level of geometric thinking relates to WODB problems. In designing the problem above, I was intentionally trying to create something aimed at students at Van Hiele's descriptive level vice the visual level. Given a student's level of geometric thinking, how might they respond to this problem? Are some WODB problems better suited for students at a visual or descriptive level or are WODB problems inherently differentiated and students at all levels can relate meaningfully to these style of problems. Another question that I've been thinking about recently is how to use WODB questions. Should I use them to introduce new terminology or to review terminology that students have already been exposed to. For example, in the problem above, I made sure to include a concave shape. Would it be more effective to wait until students learn concave and convex polygons and then reinforce it with this problem or should I introduce the vocabulary here and then talk about its definition? These are questions that I'm still exploring. Nova Scotia Mathematics Curriculum Outcomes Grade 2 G03 - Students will be expected to recognize, name, describe, compare and build 2-D shapes, including triangles, squares, rectangles, and circles. Grade 3 G02 - Students will be expected to name, describe, compare, create, and sort regular and irregular polygons, including triangles, quadrilaterals, pentagons, hexagons, and octagons according to the number of sides. Grade 4 G02 - Students will be expected to demonstrate an understanding of congruency, concretely and pictorially. Grade 5 G02 - Students will be expected to name, identify, and sort quadrilaterals, including rectangles, squares, trapezoids, parallelograms, and rhombi, according to their attributes Grade 6 G01 - Students will be expected to construct and compare triangles, including scalene, isosceles, equilateral, right, obtuse, or acute in different orientations. Grade 6 G02 - Students will be expected to describe and compare the sides and angles of regular and irregular polygons. Grade 9 G02 - Students will be expected to demonstrate an understanding of similarity of polygons. EL
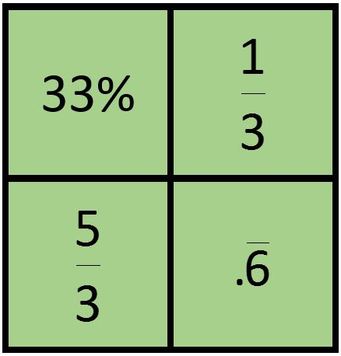
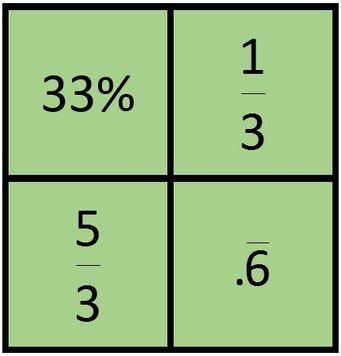
I've mentioned in the past that I think WODB questions are a great way to begin a lesson and engage students in a mathematical discussions. Below is one such question I created for grade 7 students. Most are working in or have recently finished Unit 3 on Fractions, Decimals and Percents. The question below might be a good review now that students have the language and vocabulary to debate which one doesn't belong. Here are some suggestions and why each number might not belong: Top Left: It is the only percentage and it is the only number with a tens place. It is also the only number without a vinculum. This is also the only number that is not an exact multiple of 1/3. 33% would be 33/100 and so is just a bit less than 1/3. If all the numbers were written as decimals, this would be the only terminating decimal. Top Right: It is the only number that would be a unit fraction when written as a fraction Bottom Left: It is the only value "greater than one". 33 is great than one but since it is a percentage, it represents 33/100. Bottom Right: This is the only even number and also the only term without the digit 3 in it. It is also the only number written as a decimal and the only box with just one digit in it. If your students are not used to participating in this type of discussion, you might scaffold it by first having students brainstorm and list the vocabulary and math terminology that might be used in the coming conversation. This might be especially helpful in a late French Immersion classroom where all students might not be familiar with the correct vocabulary. Having it listed on the board might help students feel more confidence in joining in the conversation. For the fractions, decimals and percent WODB above here is a list of vocabulary students might come up with: unit fraction, improper fraction, mixed number, percent, terminating decimal, non-terminating decimal, even and odd. A special thanks to Matt Murphy (@Lemurph42) for the following translation of the above post! Lequel n’appartient pas? Les Fractions, Décimaux et Pourcentages.J’ai déjà dit que je trouve les questions de WODB font un bon départ pour engager les élèves en discussions mathématiques. Ci-dessous il y a une telle question que j’ai créé pour les élèves de 7e année. La plupart de nos classes ont déjà complété chapitre 3 (fractions, décimaux et pourcentages), ou le finiront bientôt. L’exemple suivant pourrait être une bonne révision maintenant que les élèves ont le vocabulaire nécessaire pour s’engager en débat. Voici les arguments pour chaque choix : Gauche supérieure: c’est la seule pourcentage et c’est le seul nombre avec un chiffre à la position des dixaines. C’est aussi le seul nombre qui n’a pas une surlignéation. Ce n’est pas un multiple de 1/3 (33 % sera 33/100, un peu plus petit que 1/3). Si tous les nombre seront écrit comme décimal, c’est le seul qui termine. Droite supérieur: c’est le seul qui est une fraction unitaire. Gauche inférieur: le seul nombre qui est « plus grand qu’une ». C’est vrai que 33 est plus grand qu’une, mais puisque c’est une pourcentage, la valeur est 33/100 en réalité. Droite inférieure: c’est le seul nombre paire et il ne contient pas le chiffre 3. C’est le seule nombre en forme décimal et le seul qui ne contient qu’un chiffre. Si vos élèves ne sont pas habitués à tel sorte de discussions, vous pouvez utiliser l’échafaudage. D’abord, demandez aux élèves de faire un remue-ménginges du vocabulaire mathématique qui pourrait être utile dans la conversation. Ceci pourrait être utile dans une classe d’immersion tardive dont les élèves ne seront pas familiers avec tous les mots de vocabulaire. La confiance des élèves augmentera avec une liste mots disponible au tableau, faisant qu’ils seront plus capables à participer. Pour la WODB des fractions, décimaux et pourcentages en haut, voici quelques mots de vocabulaire que, peut-être, vos élèves fourniront: fraction impropre, nombre mixte, pourcentage, décimal terminé, décimal illimité, paire, impaire Nova Scotia Mathematics Curriculum Outcomes Grade 7 N07 - Students will be expected to compare, order, and position positive fractions, positive decimals (to thousandths), and whole numbers by using benchmarks, place value, and equivalent fractions and/or decimals. Grade 7 N03 - Students will be expected to solve problems involving percents from 1% to 100% (limited to whole numbers). EL
I like to start class with an opening activity that promotes discussion and gets lots of students to participate. Questions in the format of "Which One Doesn't Belong?" allow a lot of student voices to be heard. It also gives a voice to students who think outside the box. There are many different ways to answer these questions. The important part is to provide a logical reason for the item you've selected. I'm consistently impressed with the creativity of students. The WODB question below combines two of my favourite things... math and pencils!
You can find lots of great examples of this type of question on the wodb.ca website, or check out the @WODBMath twitter feed.
EL |
Categories
All
|





 RSS Feed
RSS Feed