|
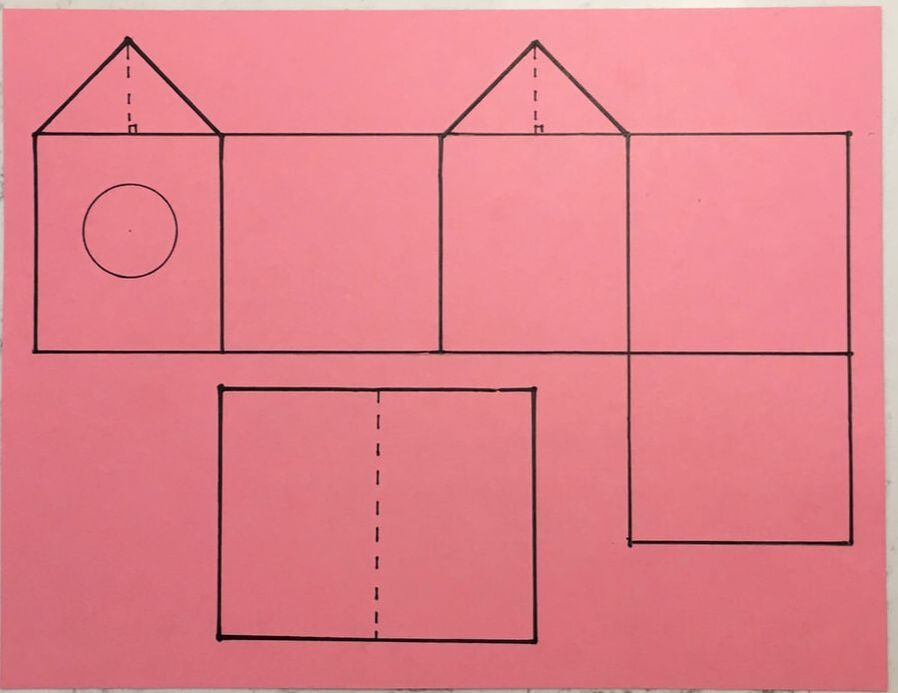
"Design and build a model birdhouse from a single sheet of 8.5" x 11" sheet of paper." This open ended activity seems simple at first but will require careful planning and attention to detail for students to be successful. You might start off this activity by showing a photo of an actual birdhouse and asking students to brainstorm the features of a good birdhouse. A website like this one might be a good guide. Next you can talk about the expectations for their model birdhouse design:
Students should then be asked to create a design. The design should minimize wasted paper (i.e. use as much of the page as possible) and be easy to assemble (i.e. minimize the number of pieces you have to cut out and assemble). You can then show students an example of a finished design. ProcedureStep 1 - Students should brainstorm some possible designs (at least two) on a piece of looseleaf Step 2 - Ask students to pick their favourite idea and share it with the teacher Step 3 - Once the teacher approves their design, students are given a piece of card stock. They can then lay out their design with a ruler Step 4 - When finished, students will measure and record all dimensions for their model. Students then calculate the surface area and volume of their design Step 5 - The final step is to cut out and assemble their birdhouse model! Here is a Google slides document that could be used to introduce the activity to students and make the expectations clear. Math at Work 10 Activity: One teacher modified this activity by giving students a selection of designs to choose from instead of designing their own (here are links to pdf template 1 and template 2). Students then did all of the measurements and computations and had to determine costs for shingles on the roof, siding for the walls and paint for the interior. Here is a handout similar to the one she used. Extensions: If you were to take your model and use it to build an actual birdhouse from wood, what would have to change? By what scale factor would you have to increase the size? How would building with 3/4" thick wood (instead of flat paper) change the size of the pieces needed? What supplies would you need and how much would it cost to build? NS Outcomes: Mathematics 9 - G01 Students will be expected to determine the surface area of composite 3-D objects to solve problems Mathematics 10 - M03 Students will be expected to solve problems, using SI and imperial units, that involve the surface area and volume of 3-D objects, including right cones, right cylinders, right prisms, right pyramids, and spheres. Mathematic at Work 10 - M04 Students will be expected to solve problems that involve SI and imperial area measurements of regular, composite, and irregular 2-D shapes and 3-D objects, including decimal and fractional measurements, and verify the solutions. Mathematics Essentials 12 - 2.4 Sketch and construct a model which will enable a student to show others some mathematics involved in a career interest EL
A couple of weeks ago, I saw a tweet from Don Fraser (@DonFraser9) in which he noticed that every box of Raisin Bran says "2 scoops" no matter what it's size is. I was recently talking with a teacher about the Percent, Ratio, and Rate unit for grade 8 math and I was reminded of Don's question. This deserved some additional investigation so I headed to the grocery store to gather the facts. At my local store, Kellogg's Raisin Bran is available in 3 sizes as seen below. Questions to Consider1. Rate: Which size box of cereal has the best unit price (g/$)? 2. Ratio: If there are two scoops in the regular size box, to preserve the same proportion of raisins, how many scoops should there be in the Family Size and Jumbo Size box? Alternatively, if the ideal proportion of raisins is to be found in a different size box, how many scoops should there be in the other two sizes? 3. Ratio: A "scoop" is a non-standard unit of measure. If the amount of raisins in each box stays the same proportion, then how should the size of the scoops change in order to maintain that proportion in each size box? 4. Volume: These boxes all have different volumes. Determine the volume of each and compare it to the weigh of cereal in that box. Does this rate stay the same? If it doesn't, what does it tell you about the amount of empty space in the box? How do the dimensions of each box compare? Are the different sized boxes similar shapes? Some additional Raisin Bran resources: Nova Scotia Mathematics Curriculum Outcomes Grade 8 M03 - Students will be expected to determine the surface area of right rectangular prisms, right triangular prisms, and right cylinders to solve problems. Grade 8 M04 - Students will be expected to develop and apply formulas for determining the volume of right rectangular prisms, right triangular prisms, and right cylinders. Grade 8 N04 - Students will be expected to demonstrate an understanding of ratio and rate. Grade 8 N05 - Students will be expected to solve problems that involve rates, ratios, and proportional reasoning. Grade 9 SP03 - Students will be expected to develop and implement a project plan for the collection, display, and analysis of data by: formulating a question for investigation; choosing a data collection method that includes social considerations; selecting a population or a sample; collecting the data; displaying the collected data in an appropriate manner; drawing conclusions to answer the question. Mathematics 12 MRP01 - Research and give a presentation on topic that involves the application of mathematics. EL
My wife and I were enjoying a peanut butter cup after dinner a few nights ago. She was eating a standard peanut butter cup (wide and short) and I was eating a miniature peanut butter cup (narrow and tall). I mentioned that the economy rate of mine was higher than hers and therefore my peanut butter cup had a higher peanut butter to chocolate ratio (the economy rate of a container is the ratio of its volume to its surface area. The higher the ratio, the more economical the container is). A 'lively discussion' ensued with a few pauses for the rolling of eyes. Time to break out a ruler, calculator, and the formula for the volume of a frustum (a truncated cone or pyramid) which is the shape of a peanut butter cup. The volume of a frustum is given by the following formula: where R and r are the radii of the top and bottom circles of the truncated cone. The formula can be derived without calculus by taking the entire cone and subtracting the tip to make a frustum. When Heron of Alexandria derived the formula for the volume of a square based frustum, he created the the Heronian mean. The Heronian mean of two numbers A and B is the weighted mean of their arithmetic mean and geometric mean. With this, he was one of the first people to encounter imaginary numbers. The formula below is the general formula for a frustum where A and B are the upper and lower base of the frustum: Lets find the total volume of the big peanut butter cup first. R = 46 mm, r = 38 mm and h = 10 mm. Therefore the volume is 55585.25 mm^3. If we assume that the chocolate is a uniform thickness of 1 mm then we can easily calculate the volume of the peanut butter by subtracting 2 mm from each measurement and recalculating giving 40346.43 mm^3. That means that the volume of chocolate is the difference of these two values or 15238.82 mm^3. This gives us a peanut butter to chocolate ratio of 2.65 Now time to measure the little peanut butter cup. R = 27 mm, r =22 mm and h = 14 mm. Given these measurements, the total volume is 26492.00 mm^3, the volume of peanut butter is 19163.72 mm^3 and the volume of chocolate is 7328.28 mm^3.
This gives us a peanut butter to chocolate ratio for the little peanut butter cup of 2.61. Nearly identical. But the thickness of the chocolate is far from uniform as this cross section shows. The chocolate is actually quite a bit thicker on top and bottom of the little peanut butter cup than on the big one. The peanut butter in the little peanut butter cup actually looks closer to a half-sphere than a frustum. So if you love the chocolate you should eat the little peanut butter cups and if you love the peanut butter, you should eat the big peanut butter cup. EL |
Categories
All
|






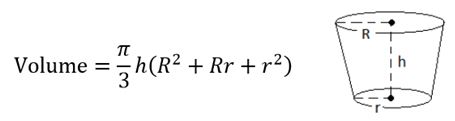
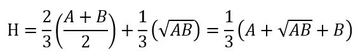


 RSS Feed
RSS Feed