|
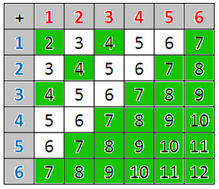
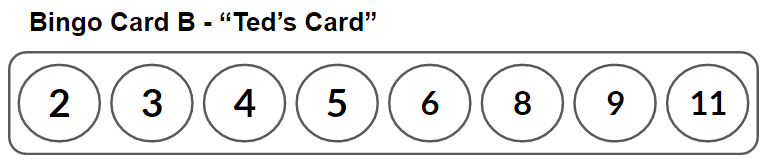
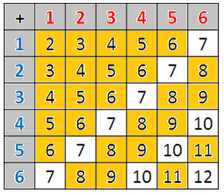
My son and I were looking through an issue of Fun to Learn Friends magazine recently and we ran across a game called "Spring Bingo". He was quite interested and wanted to give it a try. He is in grade primary and can subitize the pips on a six sided die as well as confidently sum the values on two dice. Just the skills we need to play this game. We played several times. At the end of most of the games, my son got frustrated trying to roll either a 2 or a 12. He doesn't quite understand why it takes so long to roll one of these numbers. George's bingo card has both of these numbers out of the eight numbers on the card. This seems unnecessarily cruel. Ted's card has the 2 but not the 12. This made me wonder if this is a fair game or if one of the cards has a better probability of winning. Time for some math... It appears that Card B is slightly better than Card A. I'm not sure if this would make a significant difference in the outcome of the game (i.e. rolling all the numbers on your card before your opponent does). I wonder what the average number of rolls it takes to complete each bingo card is? How much of an advantage does going first in this game give? If the player with Bingo Card A goes first does this equalize the advantage of the better Bingo Card B? These would be great questions for the Mathematics 12 research project outcome (MRPO1). To try to answer some of these questions, I thought that writing some code would be helpful. I know a grade 8 student that completed the Introduction and Intermediate Programming with Python courses from Art of Problem Solving. I contacted him and he graciously created a very nice Python program to simulate this game for me. I modified the code a bit so that it just plays one bingo card and counts how many rolls it takes to complete the card. The average number of rolls in 100,000 games for "George's Card" was 58. The average number of rolls in 100,000 games for "Ted's Card" was 48. I was a bit surprised that there was this much difference. Playing with Ted's bingo card appears to be an advantage. Next I modified the code again so that it plays the game with George going first to count how often George wins. In 100,000 games, when George went first, he won 50703 of the games. I again modified the code so that Ted plays first. In 100,000 games, when Ted went first, he won 50806 of the games. It seems that going first is an even greater advantage than having the better bingo card. What I really like about this game is that there are mathematical outcomes that can be addressed with this activity across a wide range of grade levels. At younger ages, students are practicing subitizing and adding numbers. One variation of this game is to play it solo. This might be a nice option for a math station. I found several examples of "Roll and Cover" games where students have a sheet of paper filled with numbers (from 1 to 6 or from 2 to 12) and students roll the die or dice and cover the number (with a token or a bingo dauber) when they roll it. Just do a Google search for "roll and cover math game" and you'll find lots of examples posted online.
For students looking for an opportunity for enrichment, they can make variations of this game. They could also write computer code to simulate this game (using Scratch or Python or some other language). They could also do some statistical analysis of the game to see how fair it is. There are so many options with this simple game. Nova Scotia Mathematics Curriculum Outcomes Mathematics 1 N02 - Students will be expected to recognize, at a glance, and name the quantity represented by familiar arrangements of 1 to 10 objects or dots. Mathematics 1 N09 - Students will be expected to demonstrate an understanding of the addition of two single-digit numbers and the corresponding subtraction, concretely, pictorially, and symbolically in join, separate, equalize/compare, and part-part-whole situations. Mathematics 2 N10 - Students will be expected to apply mental mathematics strategies to quickly recall basic addition facts to 18 and determine related subtraction facts. Mathematics 5 SP04 - Students will be expected to compare the likelihood of two possible outcomes occurring, using words such as less likely, equally likely, or more likely. Mathematics 6 SP04 - Students will be expected to demonstrate an understanding of probability by: identifying all possible outcomes of a probability experiment; differentiating between experimental and theoretical probability; determining the theoretical probability of outcomes in a probability experiment; determining the experimental probability of outcomes in a probability experiment; comparing experimental results with the theoretical probability for an experiment. Mathematics 7 SP06 - Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. Mathematics 8 SP02 - Students will be expected to solve problems involving the probability of independent events. Mathematics 10 Essentials G1 - Express probabilities of simple events as the number of favourable outcomes divided by the total number of outcomes Mathematics 12 P03 - Solve problems that involve the probability of two events. Mathematics 12 MRP01 - Research and give a presentation on topic that involves the application of mathematics. EL
|
Categories
All
|


 RSS Feed
RSS Feed