|
When I first started teaching, reviewing for a test meant one thing. I would stand at the front of the room and reteach each unit, section by section. I would carefully annotate important points and questions that would likely be on the assessment. After reteaching the material, I would hand out a large packet of questions for students to work on. I found that while this helped some students, many students were either bored or confused. If they didn't understand it the first time, hearing me teach it again the same way probably wasn't helping. If they already understood the material then listening to me teach it again was not helping them learn it any better. I recently ran across a couple of blog posts from MathMedic reminding me of why I do things differently now.
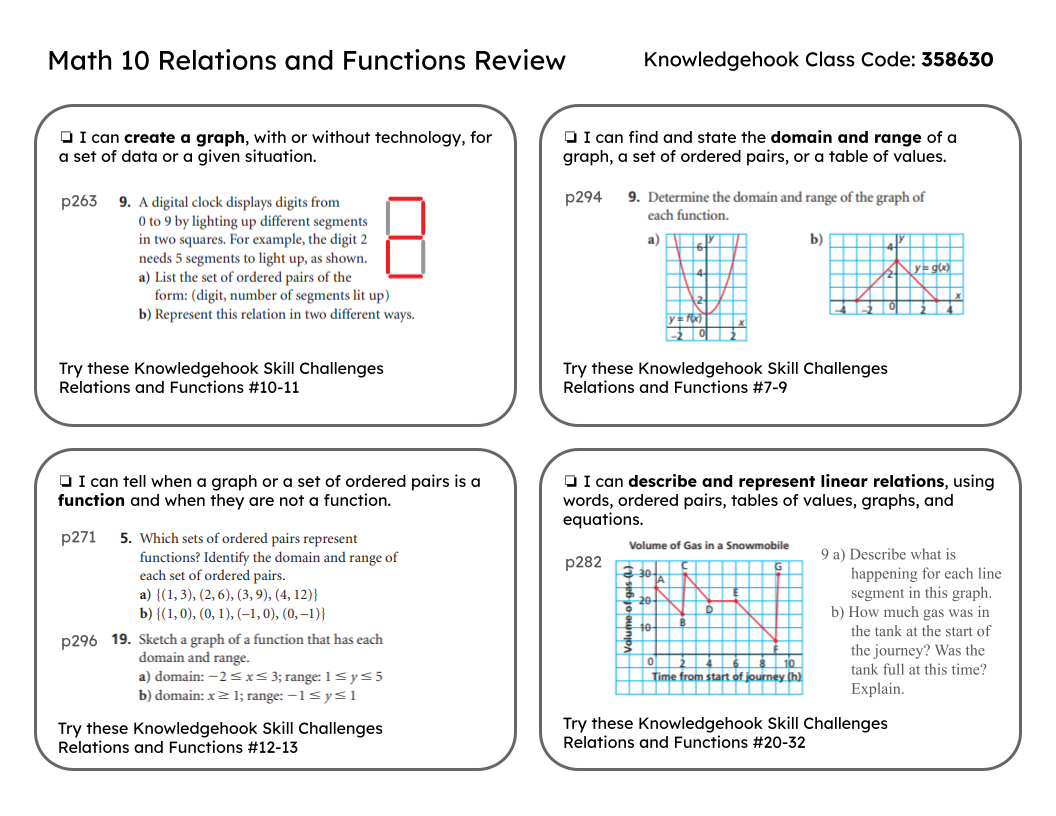
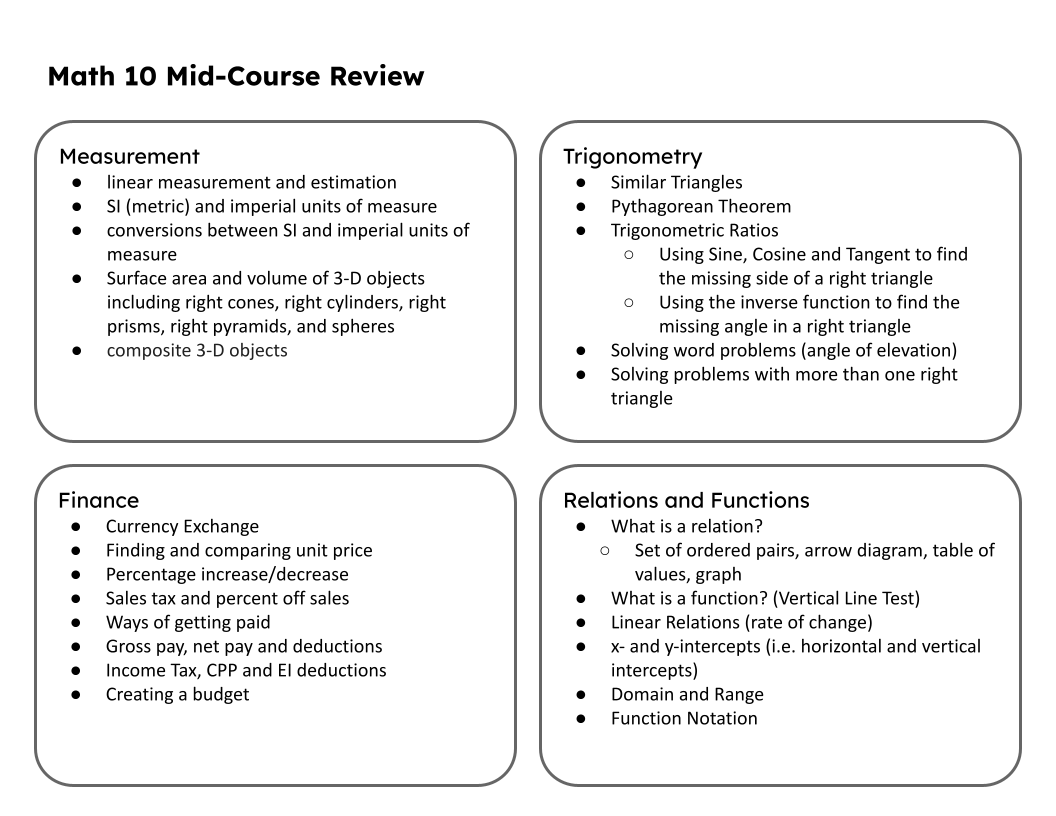
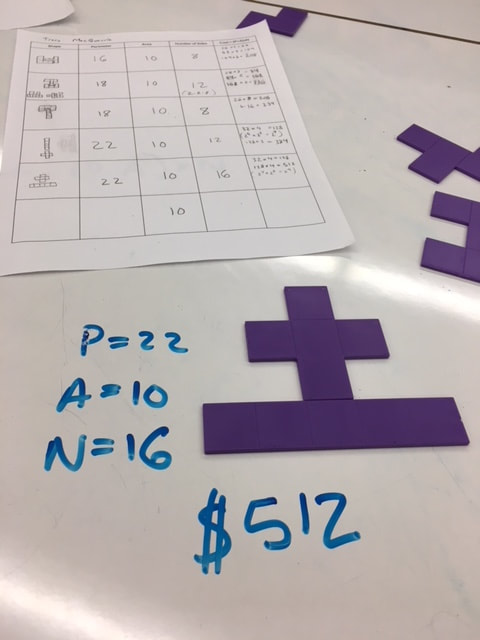
My Mathematics 10 class recently reviewed for a unit test and now we're reviewing for a cumulative assessment on the first half of the course. I typically start with some individual self-assessment where students can review outcomes and identify areas where they need additional practice or review. Next I give students a variety of ways to practice the areas they identified for themselves. Then I like to finish with a (hopefully) fun review game to wrap things ups. Student Self-AssessmentFor our Relations and Functions assessment review, I started with an overview of the outcomes for the unit so students could identify areas where they needed additional support.
Another way we reviewed was to have students in small groups at vertical whiteboards make a list of the most important topics, formula and skills from each unit. This ends up being a study sheet. After groups complete it, they share with the class to see if any groups has something that would benefit everyone. I then collosidated all of these into one class sheet that could be shared on our Google classroom. Individualized ReviewAfter this, I gave them some options to reivew and practice the areas they identified as a challenge. Sometimes this looks like the day in class we practiced domain and range.
Students that want to hear the topic being taught again have lots of options online. There are tons of YouTube channels full of teachers providing lessons on specific topics. I recently found out that a teacher from my school has his own YouTube channel with videos from our curriculum (way to go Mr. Boudreau!). There are also videos on the Nova Scotia Homework Hub, the CEMC Waterloo Courseware site, and many others. Group ReviewTo finish off, I like to play a class game where students work together to study and have some fun while doing it. A game like math basketball is a favourite in my class. We've also done self checking activities like Add 'Em Up or a Scavenger Hunt. Today for the last class of the semester before our assessment, we had a "math market" activity. Students can "buy" questions of different difficulty levels and topics from the market and "sell" solutions back for a profit.
Hopefully students learn lots and find class challenging. I still have lots to learn about teaching and am really trying new things out with my class this year. Let me know if you have a favourite review activity I should know about.
Can't Stop is a board game that was designed by Sid Sackson and released in 1980. It is a "press your luck" dice game in which players roll for dice and arranges them into two pairs. The sums of these pairs allow the player to progress their markers up the columns labeled with the values from 2 to 12. The goal of the game is to be the first to reach to top of three of these 11 columns. The height of the column is related to the probability that the sum will be rolled. The more likely the roll, the longer the column is. I was excited to find a copy of this game at a second hand shop recently. I've played Can't Stop online numerous times (at Board Game Arena) but this is a game where playing in-person seems better than virtual. The physical process of rolling and arranging the dice as well as interacting with other players makes for a better experience. I think it plays best with 2 or 3 players. They game is made for 2-4 players but I've seen people use the square plastic pieces from the game Advance to Boardwalk to add additional players in different colors. The Great Races
A nice user-created version of this paper and pencil game can be found at Board Game Geek. I like this version of the game because it is a quick game, with the "push-your-luck" aspect removed. Each player rolls just once, records their roll and then passes the dice to the next player. For a shorter game, you could play until 8 of the races are finished instead of completing all 11. Game at a GlanceBecause all the information about the game is contained on the game board, this is an excellent game for "Game at a Glance." Chad Williams has a collection of Game at a Glance images on his website, Beyond the Algorithm. Students are shown an image of a game in progress and could be asked a variety of questions.
I recently went camping and took this game along with me. I taught the game to several people (including kids) and because of the simple rules, they were all able to learn it in just minutes. Because all the pieces are plastic, they didn't blow away in the wind and if it got dirty, it could be easily rinsed off and cleaned. I think that this game would make a great addition to a mathematics classroom collection. What are your favourite games for the math classroom? Let me know! Nova Scotia Mathematics Curriculum Outcomes Mathematics 12 LR01 - Analyze puzzles and games that involve numerical and logical reasoning, using problem-solving strategies. Mathematics at Work 12 P01 - Students will be expected to analyze and interpret problems that involve probability. Mathematics at Work 11 N01 - Students will be expected to analyze puzzles and games that involve numerical reasoning, using problem-solving strategies. Mathematics Essentials 10 G4 - Compare predicted and experimental results for familiar situations involving chance, using technology to extend the number of experimental trials. Mathematics 8 SP02 - Students will be expected to solve problems involving the probability of independent events. Mathematics 7 SP06 - Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. EL
Auctions can be a fun and engaging activity in math class. The first auction I ever tried with a class was a unique bid auction that I learned about from Dan Meyer. I called it a "Lone Wolf" auction after seeing a discussion about this type of auction from Shawn Cornally. Students really enjoyed it and it generated some great discussions about strategies. We collected some data and were able to look at some displays to analyze the game. I haven't used many auctions as part of a mathematics activity. I was always concerned that too much time would be taken up by the logistics of the auction and there would not be enough time devoted to mathematical analysis. I learned some strategies for focusing on mathematical reasoning by reading how other teachers have facilitated auctions to make engaging math activities. Here are a few below: Function AuctionSarah Carter created a function auction activity for students to deepen their understanding of what makes a relation a function. Students bid on lots containing a variety of relations... some functions and some not. The team with the most functions at the end of the auction wins. Students work as a team to try to identify which lots contain the most functions and what a reasonable price for each lot might be given their starting funds. Sarah found this to be more engaging than a traditional function/not-function worksheet. The activity generates a lot of student conversation and discussion about functions. Dice AuctionNat Banting created a dice auction activity to get students thinking about the probabilities of outcomes when rolling two dice (this activity was won the 2020 Rosenthal Prize). In his description of the activity, Nat makes sure to include plenty of time for student teams to discuss their strategy and to try to assign a reasonable price to each event. He also builds in some reflection questions for students to answer at the end of the activity. This activity reminds me somewhat of the Borel Dice board game. Definite Integral AuctionI decided that an auction might be an engaging way for students to practice evaluating definite integrals in calculus class and so I created a definite integral auction activity. I incorporated some of the ideas from both Sarah's and Nat's auction activities. My auction is described below. As in Sarah's activity, I included time for students to talk and strategize by starting with five minutes to review the "auction catalogue". This page shows all the values that will be auctioned. As in Nat's auction, I scheduled in time at the halfway point for students to assess their situation and review the remaining lots. This gives students time to calculate their current integral and determine how they might increase its value even further. I also included some of Nat's reflection questions at the end to consolidate the activity. I got some additional ideas from Lola Morales (@lolamenting) when she posted on Twitter how she was going to use this activity in her classroom. If you have any tips or suggestions about auctions in math class, I'd love to hear about how you facilitate these types of activities. EL
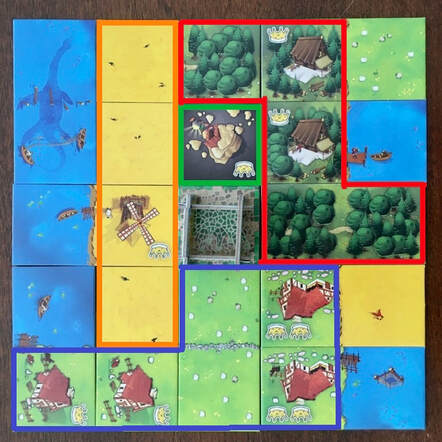
Working from home and looking after an 8 year old at the same time throughout the past three months has proven to be complicated. Providing an enriching, engaging and educational home environment for my son while still attending to work deadlines and schedules has been a difficult balancing act. A provincial state of emergency required us to adapt our daily routines. One positive change has been playing board games. My son and I have played daily board games and card games. We have gone from simple children's games such as Snakes and Ladders to more complex European-style board games like Alhambra. Our favourites (and most played) games have been: Splendor, Tiny Towns, and Kingdomino. These games give players lots of opportunities to use spatial and numeral reasoning to make informed choices. These games all work well as two player games or with larger groups. Playing KingdominoA game that I have come to appreciate is Kingdomino. It is easy to learn, quick to play and has complex strategy. In this game, players take turns drafting domino shaped tiles to add to their kingdom. Players have to build within a size constraint. Players start with a 1x1 home castle tile and your kingdom, including this home tile, can not exceed 5x5 (meaning you can add a maximum of 12 tiles to your kingdom). This size constraint means that if your kingdom is not well planned, you might end up with empty spots that can't be filled. The goal is the maximize the value of your kingdom at the end of the game. To calculate the final value, you multiply the area of each contiguous region of a single terrain type by the number of crowns contained in the region (there are six different terrains types: pastures, wheat fields, lakes, mines, forests, and swamps). If a region doesn't have any crowns in it, it scores zero points (e.g. there is a region of 4 lakes in the kingdom below but because it has zero crowns, it scores 4x0=0 points). There are four different regions with crowns in the kingdom below. The wheat field (outlined in orange) scores 4x1=4 points. The pasture (outlined in blue) scores 6x6=36 points. The forest (outlined in red) scores 5x2=10 points. And finally, the mine (outlined in green) scores 1x1=1 point. This gives a total values of 4+36+10+1=51 points... a decent total score. Bringing Math to the SurfaceWhen I first looked at the mathematics applied in this game, I only considered adding up the scores to determine a winner at the end. Playing this game with my son however led me to see how mathematical decision are used throughout the game. Each turn, you must decide which domino (or dominoes if you're playing with two people) you will select for your kingdom. In order to bring mathematical reasoning to the surface, I began reasoning out loud. This let my son hear all the considerations that go into my selection. Given the growing kingdom below, which of the four dominoes would you select and why? The first domino doesn't have any crowns, but it could be added to the bottom of the kingdom to make a region of 4 wheat fields where crowns could be added on a future turn. The first domino also gives me the benefit of going first next turn (dominoes are placed in order from top to bottom each turn). The second domino has a crown in a forest. This could be added to existing region of 3 forest that has 2 crowns already. This would turn your forest region from scoring 3x2=6 to 4x3=12... a gain of 6 points. The third domino would be even better. Playing it in the bottom right would still gain you the 6 points in the forest region but also turn your 2 point lake region in to a 3 point lake region. The last domino could add a crown to your lake region and a space to your forest region. This would make the forest region worth 8 (a gain of 2) and your lake region worth 6 (a gain of 4). Looks like the third tile would give us the most immediate gain in score (a gain of 7). ProbabilityOlder players will also need to consider the unequal distribution of terrain types and crowns. There are lots of wheat fields (26) but only 5 have a single crown. There are 14 pastures but two of these have one crown and two have double crowns. Mines are rare with only 6 of them in the game but they can generate big scores. Three of the mines have double crowns and one mine has the only triple crown in the game. The trick is to grab them when you can and place them next to each other. Strategy vs. LuckThere is a fair amount of luck in this game. The dominoes are shuffled and show up in random order. If you have the first pick in the round you can get a great tile but if you go last, you may get stuck with a tile that you don't really want. Also, if you're not playing with four players, you won't be playing with the full set of dominoes. A domino you were hoping to get might not even be in the game. With that being said, there is enough strategy to keep both kids and adults thinking critically about their decisions throughout the game. Playful MathI think this is a great example of a board game that demonstrates a playful and entertaining way to practice mathematical skills and reasoning. It's easy to learn rules and quick play time make it a great choice for playing with younger family members. It has been in regular rotation with my family during our at home learning. If you want to quickly learn how to play Kingdomino, you can watch Rodney Smith's Watch It Played video on YouTube. I have come to appreciate how much skill there is to teach an 8 year old, with limited patience, the rules to a new board game. If you want some tips on teaching your kids (or friends) how to play a new game, I highly suggest Shut Up & Sit Down's video How to Teach Board Games Like a Pro. A lot of these tips apply equally to the classroom and teachers will be able to see how good pedagogy is universal. EL
Summer is here and I've recently returned from a family vacation that included several lengthy flights. My son just turned eight years old and enjoys flying but can get a bit restless after a few hours on an airplane. Below are a few of the games and activities that we packed to make the time pass enjoyably. These games are best when they are small, lightweight, easy to pack and can be played on the limited space of an airplane tray table (often around 16.5" x 10.5" but there is no standard size). Games are ideally two player but if you're on a larger plane, you might be able to play a three player game. Pencil and Paper GamesGames that can be played with just pencil and paper are ideal for an airplane. We bring a few pencils and a tablet of paper with us for games, sketching or making notes. Here are a few of our favourite pencil and paper games:
Games with Dice, Cards and Counters
Commercial Board Games
Other StuffWhen on a long play ride I also bring snacks, a small LEGO set, and some art supplies to draw or colour with. Do you have suggestions for travel games to play with with your children? I'd love to hear your suggestions. EL
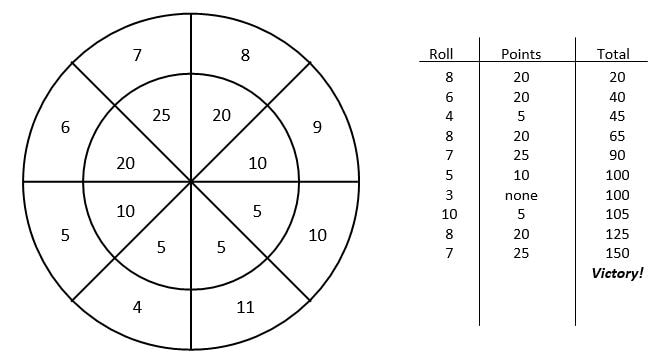
Below is a simple probability game that I've played with students for many years in a number of different courses. I don't really remember where I got it from but if you've seen it before, I'd love to know where it originated. I've found that students enjoy it and they really develop some good ideas about probability. Its similar to the Two-Dice Sum Game from Marilyn Burns but with some additional mental math for older students. InstructionsThis is a game for two or more players. Each player creates their own score card by drawing two concentric circles and then divide it into eight sectors. Choose eight different numbers between 2 and 12 and place them in the sectors in the outer ring. In the inner ring of the circle place numbers that add up to 100 (it is easiest to stick with multiples of 5). Roll two dice and add the numbers together, if the total is one of the numbers in the outer ring of your score card, you score that numbers value (the number in the inner ring). Players alternate rolling and scoring on their card until one of the players has 150 or more points (or to 100 for a bit shorter game). A google doc handout for this is available here. Sample Score CardTypically, the first time students play, they will randomly select numbers and values for each sector. After students have had the chance to play a few games, stop and ask them to look at different score cards to see if there any common characteristics of winning cards. What makes a good score card? Is it all just luck or are some cards better than others? Developing a StrategyWhat makes a good score card? Here are some common student observations:
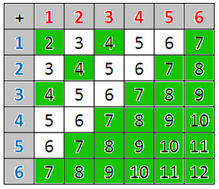
Experimental ProbabilityYou might ask students to roll two dice a bunch of times and record which numbers come up each time. Create a bit dot plot or a bar graph at the front of the classroom using all of this data. Ask students to predict what the shape of this graph will be. You could also use an online tool to model lots of dice rolls to see how it compares to the class data. You could then discuss the theoretical probability for each sum and compare it to the data you gathered. I always find this a fun activity and a nice way to start a discussion about probability and strategy. A nice question to start the class on the following day would be a Would You Rather? math prompt, "Would you rather flip 2 coins and win if they match OR roll 2 dice and win if they don't match?" Another great follow up activity would be Don Steward's Dice Bingo. Nova Scotia Mathematics Curriculum Outcomes Mathematics at Work 12 P01 - Students will be expected to analyze and interpret problems that involve probability. Mathematics Essentials 10 G4 - Compare predicted and experimental results for familiar situations involving chance, using technology to extend the number of experimental trials. Mathematics 8 SP02 - Students will be expected to solve problems involving the probability of independent events. Mathematics 7 SP06 - Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. EL
An engaging puzzle with simple instructions is to ask students to create a rectangle using pentomino pieces. Let them figure out what rectangle dimensions are possible given the total number of squares in the pentominoes they're using (for a full set of 12 pentominoes, 3x20, 4x15, 5x12 and 6x10 are possible). You can also print off a variety of other shapes and challenge students to fill those shapes with pentominoes or have students create their own shapes and challenge their friends to solve them. Younger students can be challenged to fill an empty picture frame or tray with pentominoes. Here are five great games, puzzles and activities (in no particular order) that use pentominoes:
2. Pentomino Puzzles from Jon Orr (@MrOrr_geek) - Jon describes an activity where students are given a hundreds chart and a transparent pentomino. Ask students to place their pentomino on the hundreds chart so that it covers a sum of 135. Then ask students to share their strategies for finding the correct placement. Are there sums that are not possible to achieve? Continue the activity by selecting different tiles, giving different sums to find, creating equations and solving them. I also saw these questions posted by Amie Albrecht (@nomad_penguin) on twitter, "Can you find a pentomino that covers numbers that: sum to 150, sum to an even number, covers three multiples of 4, and more". Jon created an online Desmos Activity that allows you to do this activity virtually. 3. Pentomino Farms - I was introduced the the pentomino farms activity from Martin Gardener's book Knotted Doughnuts and Other Mathematical Entertainments. The task is to use the 12 pentominoes to build a fence around a field on your farm. The rule used to join the pentominoes to form a fence is that they must touch along the full edge of a square and not just at the corners. There are four types of farms to create. For each type, what's the largest field you can enclose?
4. How Convex is a Pentomino? - Which pentomino shape is the most convex? How do you measure "convexity"? This is an interesting question that generated lots of discussion on Twitter. Some interesting methods of measuring this were discussed by Alexandre Muñiz (@two_star) in his blog post, "Vexed by Convexity." I think it would make a great discussion for students to rank the pentominoes by convexity and then defend their choices.
If you have a favourite activity, puzzle or game featuring pentominoes, I would love to hear about it! EL
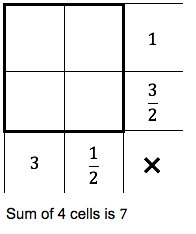
Practice is important. Whether it is playing the piano, shooting free-throws, popping an ollie or solving a quadratic equation you need to practice to improve. Some practice routines are more effective than others at helping students solidify their understanding. Practice can often seem tedious and it can be difficult to maintain the motivation to practice. In mathematics, students practice skills in a variety of ways. One style of practice that can help students stay motivated and engaged is purposeful practice. Instead of a page full of repetitive problems, students focus on an activity that has a mathematical goal to achieve. Dan Meyer wrote a blog post a few years ago titled "Purposeful Practice & Dandy Candies" that started me thinking about how to make activities in my classroom more purposeful. Open MiddleOne of my favourite sources of problems with purposeful practice is Open Middle. There is a large selection of questions organized by topic and grade level. Each question has an "open middle" meaning there are many ways to explore and solve the problem. Below is a question submitted to the Open Middle site by Robert Kaplinsky. In this question, students try to find the arrangement of digits that yields the product closest to 50. Students will try numerous different arrangements of digits and get lots of practice multiplying decimal numbers without it seeming tedious. The question can also be quickly modified to give additional practice. For example, just add a hundredths place onto one of the factors and use 5 different digits. Math GamesGames can be a great way to encourage students to practice. There are lots of examples of but I'm going to mention just two. The first goes by several names. Joe Schwartz wrote a great post about Factor Captor. A similar game is described on the NCTM Illuminations site called the Factor Game. Students alternate turns playing on board filled with numbers. The first player selects a number to cover and adds that number to their score. The second player finds all the factors of that number, covers them and totals those number to add to their score. The roles are then reversed and play continues until there are no uncovered numbers remaining. There is a lot of math in this game and it is fun to play. The second game is Horseshoes from Math4Love. This game is played with a deck of cards numbered 1-9. Two cards are drawn to form a two-digit target number. Then four more cards are drawn. Players use these four digits to create an equation using addition and subtraction that is as close as possible to the target number. For example, let's say that the target number is 25 and the four digits given are 1, 3, 6 and 9. A student might create the equation 39-16 = 23. Another student might make the equation 13+6+9 = 28. There are lots of way to tweak this game for different levels of complexity. Both of these games allow for lots of numerical practice in a format that engages students. There are many excellent sources of ideas for mathematical games. My current 'go-to' resource is a book titled Well Played, 6-8. Math PuzzlesThere are several mathematical puzzles that include lots of practice with numerical computations in pursuit of a solution. KenKen puzzles and Maze 100 from NRICH are two such puzzles that I've used. I also think that Yohaku puzzles are great. They are numerical puzzles where you need to determine the number that is in each square in order to make the column and row sum/products.
Desmos ActivitiesFor classrooms with the available technology, activities from Desmos.com are another way to practice with purpose. An activity that incorporates a lot of meaningful practice is Marbleslides. In this activity, student try to capture stars on a Cartesian grid by creating a path using functions that marbles roll down. Students work to refine their functions to capture as many marbles as possible. Another activity that generates lots of practice is Transformation Golf. Students use a series of rigid transformations to move a shape to specified location. They have to find an efficient path around several obstacles. Each successive challenge increases in complexity. IncentivesThere are also activities that have a non-math goal for students to achieve. Lots of online math games have incentives for students such as badges to earn, experience points to accumulate or virtual prizes to win. There are also worksheets and activities with non-math goals. Worksheets such as "Algebra with Pizzazz" and "Punchline Algebra" have a riddle to be solved once all of the questions are completed. In my classroom practice, I used a number of activities with these types of incentives and I think that many students find them exciting and fun. If students are excited to do math, I consider that a win. However, I think that these types of activities should be used with caution. We don't want to inadvertently send a message to our students that math isn't fun by itself so we have to disguise it (like sneaking vegetables into their favourite foods so kids will eat them). Please Share!If you have a favourite math activity, game or puzzle that gets students practicing math with a purpose, I'd love to hear about it. Please leave me a comment. EL
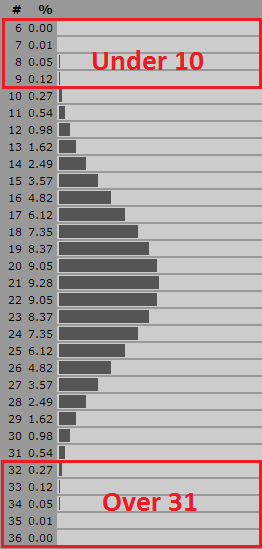
My son and I recently spent a lovely fall afternoon exploring the carnival games and amusement rides at a local fair. My son is quite adventurous when it comes to amusement park rides and is eager to try just about any ride that he meets the height requirement for. While we were walking through the midway, I spotted a carnival game called "Roll Down" that appeared to have a bit of mathematics involved. The object of this "game of skill" is to roll six balls down and inclined ramp to land in one of six numbered bins. If the sum of the six rolls is under 10 or over 31, you win. Is this game worth the $5 price to play? What are my chances of winning? Should I go for under 10 or over 31? Is this just a carnival scam or is there some skill involved? The bins are just wide enough for a ball to fit so it is very difficult to aim a ball with accuracy. You also have to question if the balls roll straight and if the board is smooth and level. Lets just assume that the balls fall into a random bin (you could then play an equivalent game at home by rolling 6, six-sided dice). With six balls, the smallest sum possible is 6 (all 1's) and the largest is 36 (all 6's). How many ways are there to get each possible value? There are only 31 possible sums (6-36) that you can score. To roll a sum of under 10, you can score 6, 7, 8 or 9. To roll a sum of over 31, you can score 32, 33, 34, 35, or 36. At first glance, it looks like you have a 9/31 chance of winning but this is not correct.
This reminds me of a bet in the casino game craps that looks good, but on further inspection is really bad. The field bet is a bet on the sum of the next roll of two six-sided dice. If the sum of the two dice is 2, 3, 4, 9, 10, 11 or 12 you win. If the sum is 5, 6, 7 or 8 then you lose. It has the illusion that there are more ways to win than lose, but you are much more likely to roll one of the losing numbers. With practice at Roll Down, you might be able to achieve better than the random results that I detailed above. Instead of this practice, I decided to spend my $5 at the concession stand to buy a hand-battered, deep fried corn dog. A midway concession stand can also be considered a bit of a gamble, but in this case it was a delicious win! EL
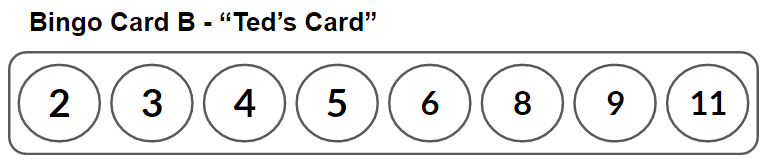
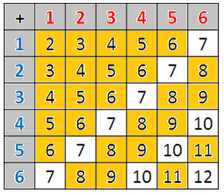
My son and I were looking through an issue of Fun to Learn Friends magazine recently and we ran across a game called "Spring Bingo". He was quite interested and wanted to give it a try. He is in grade primary and can subitize the pips on a six sided die as well as confidently sum the values on two dice. Just the skills we need to play this game. We played several times. At the end of most of the games, my son got frustrated trying to roll either a 2 or a 12. He doesn't quite understand why it takes so long to roll one of these numbers. George's bingo card has both of these numbers out of the eight numbers on the card. This seems unnecessarily cruel. Ted's card has the 2 but not the 12. This made me wonder if this is a fair game or if one of the cards has a better probability of winning. Time for some math... It appears that Card B is slightly better than Card A. I'm not sure if this would make a significant difference in the outcome of the game (i.e. rolling all the numbers on your card before your opponent does). I wonder what the average number of rolls it takes to complete each bingo card is? How much of an advantage does going first in this game give? If the player with Bingo Card A goes first does this equalize the advantage of the better Bingo Card B? These would be great questions for the Mathematics 12 research project outcome (MRPO1). To try to answer some of these questions, I thought that writing some code would be helpful. I know a grade 8 student that completed the Introduction and Intermediate Programming with Python courses from Art of Problem Solving. I contacted him and he graciously created a very nice Python program to simulate this game for me. I modified the code a bit so that it just plays one bingo card and counts how many rolls it takes to complete the card. The average number of rolls in 100,000 games for "George's Card" was 58. The average number of rolls in 100,000 games for "Ted's Card" was 48. I was a bit surprised that there was this much difference. Playing with Ted's bingo card appears to be an advantage. Next I modified the code again so that it plays the game with George going first to count how often George wins. In 100,000 games, when George went first, he won 50703 of the games. I again modified the code so that Ted plays first. In 100,000 games, when Ted went first, he won 50806 of the games. It seems that going first is an even greater advantage than having the better bingo card. What I really like about this game is that there are mathematical outcomes that can be addressed with this activity across a wide range of grade levels. At younger ages, students are practicing subitizing and adding numbers. One variation of this game is to play it solo. This might be a nice option for a math station. I found several examples of "Roll and Cover" games where students have a sheet of paper filled with numbers (from 1 to 6 or from 2 to 12) and students roll the die or dice and cover the number (with a token or a bingo dauber) when they roll it. Just do a Google search for "roll and cover math game" and you'll find lots of examples posted online.
For students looking for an opportunity for enrichment, they can make variations of this game. They could also write computer code to simulate this game (using Scratch or Python or some other language). They could also do some statistical analysis of the game to see how fair it is. There are so many options with this simple game. Nova Scotia Mathematics Curriculum Outcomes Mathematics 1 N02 - Students will be expected to recognize, at a glance, and name the quantity represented by familiar arrangements of 1 to 10 objects or dots. Mathematics 1 N09 - Students will be expected to demonstrate an understanding of the addition of two single-digit numbers and the corresponding subtraction, concretely, pictorially, and symbolically in join, separate, equalize/compare, and part-part-whole situations. Mathematics 2 N10 - Students will be expected to apply mental mathematics strategies to quickly recall basic addition facts to 18 and determine related subtraction facts. Mathematics 5 SP04 - Students will be expected to compare the likelihood of two possible outcomes occurring, using words such as less likely, equally likely, or more likely. Mathematics 6 SP04 - Students will be expected to demonstrate an understanding of probability by: identifying all possible outcomes of a probability experiment; differentiating between experimental and theoretical probability; determining the theoretical probability of outcomes in a probability experiment; determining the experimental probability of outcomes in a probability experiment; comparing experimental results with the theoretical probability for an experiment. Mathematics 7 SP06 - Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. Mathematics 8 SP02 - Students will be expected to solve problems involving the probability of independent events. Mathematics 10 Essentials G1 - Express probabilities of simple events as the number of favourable outcomes divided by the total number of outcomes Mathematics 12 P03 - Solve problems that involve the probability of two events. Mathematics 12 MRP01 - Research and give a presentation on topic that involves the application of mathematics. EL
|
Categories
All
|






























 RSS Feed
RSS Feed