|
Brian Bolt has written numerous resource books for teachers containing collections of rich mathematical problems, puzzles, investigations and games. Some are descriptions of classic problems and puzzles while others are new creations. I think these books are a great resource and I wanted to share three of my favourite problems from them. Number the Sectors
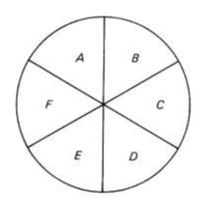
This is problem #53 from Even More Mathematical Activities (1987) and problem #72 from The Mathematical Funfair (1989). Instead of starting by asking students to find a set of numbers that gives all the integers from 1 to 25, I like to create an example as a class and then challenge them to do better (get to a larger number). You can also ask them to prove what the maximum value is. Bolt has an alternate version of this puzzle in A Mathematical Pandora's Box (1993) (#12 Can you Do Better), which has 5 sectors around a central circle. This version can be found online at NRICH Maths as the Number Daisy. How Large a Number Can You Make?Make the largest number with just the digits 1, 2, and 3 once only once and any mathematical symbols you are aware of, but no symbol is to be used more than once. The challenge is to see who can make the largest number. Here are some numbers to get the ball rolling: This is problem #83 from Even More Mathematical Activities, (1987). I've given this as a warm-up problem for high school students and this often leads to a discussion of how to know which is bigger, 2^(31) or 3^(21)? Make a CenturyPut arithmetical signs in suitable places between the digits to make the following sum correct: 1 2 3 4 5 6 7 8 9 = 100 There is more than one solution. See how many you can find. This is problem #127 from Mathematical Activities (1982). I would start this challenge with students by asking them to make an expression using the numbers from 1 to 9 to make a value as close as possible to 100. I would then add on the challenge to try to find an expression exactly equal to 100. There is a very similar problem called Make 100 on NRICH Maths. I saw an earlier version of this as problem #94 in Amusements in Mathematics (1917) by Henry Ernest Dudeney. In Dudeney's version, he includes an additional challenge to try to find a solution which "employs (1) the fewest possible signs, and (2) the fewest possible separate strokes or dots of the pen. That is, it is necessary to use as few signs as possible, and those signs should be of the simplest form. The signs of addition and multiplication (+ and ×) will thus count as two strokes, the sign of subtraction (-) as one stroke, the sign of division (÷) as three, and so on." What are Your Favourite Problems?Do you have a favourite problem or puzzle from one of Brian Bolt's puzzle books? Do you have other favourite collections of puzzles? EL
Comments are closed.
|
Categories
All
|
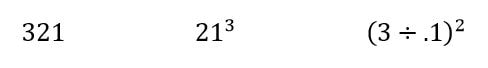
 RSS Feed
RSS Feed