|
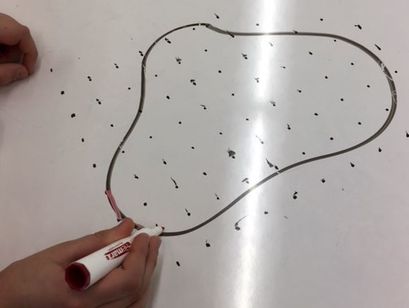
I prepared a lesson plan to work with a student. I carefully considered how I would introduce the topic, the path that the lesson might take and the questions that I would ask to prompt our discussion. I thought about the manipulatives that we might use to visualize and physically interact with the problem. I had a course carefully laid out. I started by drawing an irregular, kidney shaped area on the desk and asked the student how he would estimate the area of the shape. I was prepared for a number of different responses that I thought I might hear... but the student didn't follow my carefully plotted course for our lesson. Instead he replied, "I'd use Pick's Theorem." I grew up sailing on the Columbia River. When changing course on a sailboat, you can either turn the bow (the front of the boat) through the wind (i.e. tacking) or you can turn the stern (the back of the boat) through the wind (i.e. jibing). When tacking, the boom gently moves from from one side of the boat to the other. Jibing on the other hand can be dangerous as the boom suddenly jumps to the other side of the boat. When the student suggested Pick's Theorem, it felt like changing course by jibing instead of by tacking.
After our excursion through Pick's Theorem we found our way back to estimating the area with some manipulatives. First we covered the shape with square tiles and then we covered the shape with pennies. We found that we could cover the shape with 66 square tiles. I asked the student how the area we found with Pick's Theorem and the area we found with square tiles compared. Through our discussion we decided that we needed a common way to talk about these areas so we converted both to square centimeters. We found that the area from Pick's Theorem was 382.5 cm^2 and the area using square tiles was 412.5 cm^2. Next, we looked at our penny solution. We looked up the diameter of a penny online and found that 135 pennies at 2.85 cm^2 each gave us a total area of 384.75 cm^2. While discussing how this estimate compared to our others, the student started talking about Alex Thue and his theorem on circle packing (this student has a really good memory). The student remembered that the efficiency of hexagonal packed pennies was about 91%. So we used this efficiency to correct our penny estimate to make it even better. This led to another discussion that I hadn't planned on about tesselations and polygons that tile the plane. The student said he had read in a book that there were 14 irregular pentagons that tile the plane. His book was a few years old however so he didn't know that a 15th pentagon had been discovered in 2015 or other recent work in this area. While the lesson didn't go quite as I had planned, I was really happy to be able to take the student's contributions to the discussion and weave them into the overall narrative of our work. Being flexible, listening to students and incorporating their contributions into a discussion can sometimes throw you off course and you might end up someplace unexpected. The journey along these altered courses however can be incredible. EL
Comments are closed.
|
Categories
All
|



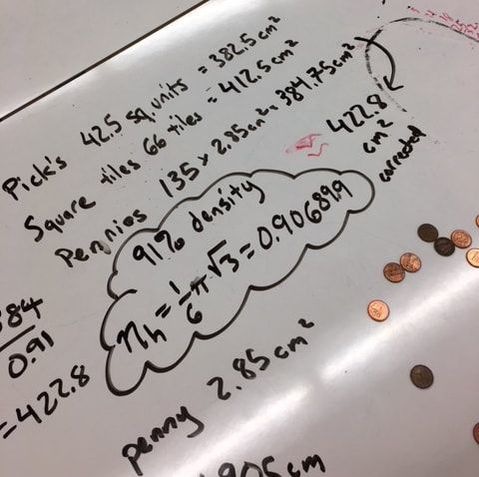
 RSS Feed
RSS Feed