|
Multi-link cubes are an incredibly versatile manipulative for mathematics class. You may see these 2 cm interlocking cubes referred to by several different names including: linking cubes, multi-link cubes, Snap cubes, Cube-a-Links and Hex-a-Link. It's a manipulative that I've seen used at nearly every grade level from Primary to 12. Recently, John Rowe (@MrJohnRowe) stated a conversation on Twitter about math manipulatives. The conversation prompted me to reflect on how I've used manipulatives, and especially multi-link cubes, as part of instruction and inquiry. I thought it would be nice to list a few of my favourite examples here: Speedy Squares from Mary Bourassa (@MaryBourassa) Speedy Squares is an activity that asks students to predict how long it would take them to build a 26 x 26 square out of linking cubes. Students start by building smaller squares and recording their times. They can then use this time to extrapolate an answer. Students could use quadratic regression to make a more accurate prediction. Jon Orr (@MrOrr_geek) also blogged about this activity and how he introduced it to his class. NS Outcomes: Math Extended 11 RF02, PCAL 11 RF04 and Math 12 RF01
Skyscraper Puzzles from Brainbashers This is a logical reasoning puzzle that you can play with just pencil and paper. The game become more focused on spatial reasoning when you actually build the towers using multi-link cubes. Lots of educators have written blog posts about how they use this puzzle in their math classrooms including Mary Bourassa, Sarah Carter, and Amie Albrecht. Mark Chubb (@MarkChubb3) has blogged about this puzzle and shared some great templates for using with multi-link cubes. NS Outcomes: Math at Work 10 G01, Math 11 LR02 Orthographic Projections from Jocelle Skov (@mrs_skov) Each student creates a 3D object using multi-link cubes. Next they draw the top, front and side views of their object. Once every student has finished the three views of their object, they trade drawings with another student. That student then tries to build the 3D object in the drawing. They check their work with the original object on the teachers desk. NS Outcomes: Math 8 G01, Math at Work 11 G03 3D Linear Relations inspired by Alicia Potvin (@AliciaPotvin1) Each group of students builds three terms of a linear pattern using multi-link cubes. Ask students to use one colour for the part of the pattern that stays the same and another colour for the part of the pattern that changes. Groups then rotate through the room and for each pattern, record a table of values, a graph and the equation. You could also ask students to determine how many cubes would be in the 43rd term as suggested at http://www.visualpatterns.org/. NS Outcomes: Math 9 PR01, Math 10 RF04
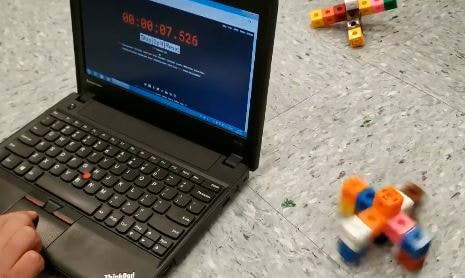
Mean, Median, Mode and Range with Linking Cubes from Jana Barnard and Cathy Talley Ask each student to reach into a large box of linking cubes to grab as many as they can with one hand. Students then build a tower with their linking cubes. As a class, students organize their towers in order from shortest to tallest. To get the class range, subtract the height of the shortest tower from the tallest tower. Is there a height that occurs more often than any other? That is the mode. To get the median, find the tower in the middle of the row (if an even amount of towers, average the two middle towers). To get the mean, even out all the towers until they are the same height saving any "left over". Suppose you had 12 towers, each with a height of 10 and 5 remainder cubes. This would give a mean of 10 and 5/12 cubes. NS Outcomes: Grade 7 SP01 Spinners from Shaun Mitchell and Mike Wiernicki (h/t Jen Carter) Students, in small groups, design a spinning top made of multi-link cubes. The goal is to design a top that spins the longest. Once the group settles on their design they collect some data. They spin the top and record the time it spins in seconds to the nearest hundredth (or tenth). They do this three or four times and then average the time (hence they have to add three or four decimal numbers and then divide that decimal by 3 or 4). They could also model their decimal numbers using decimal squares. NS Outcomes: Grade 6 N08, Grade 6 SP02 A few links to some documents that provide some additional suggestions for using linking cubes:
The examples above are mostly from secondary math classes. Multi-link cubes are also incredibly useful in elementary math classes (counting, measuring with non-standard units, composing and decomposing numbers, etc). What are your favourite linking cube activities? Let me know and I'll add them to this post. EL
Comments are closed.
|
Categories
All
|






 RSS Feed
RSS Feed