Fraction Talks Clothesline

This activity is a mashup of two instructional strategies that I really like: Fraction Talks (http://www.fractiontalks.com/) and Clothesline Math (https://mathprojects.com/clothesline-math/).

I did this activity recently with a group of Junior High math teachers.  I started by showing them a picture of the square shape at right (from the Fraction Talks website) with one of the sections shaded.  I asked them, "What fraction of this square is shaded?"  Being teachers, they were quickly able determine that the shaded area was 3/16 of the total shape. Their answers however, were not nearly as interesting as how they got their answers. I asked a number of participants to explain their methods and reasoning.  

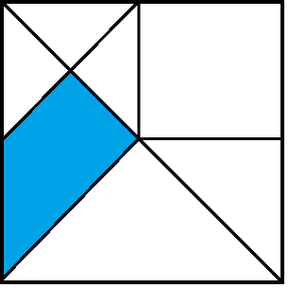
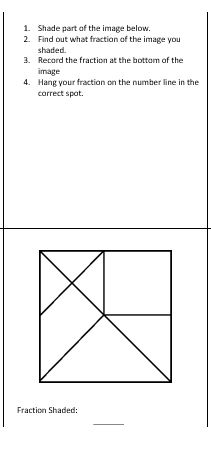
There are a lot of different ways to get to the answer and it is great for participants to see the variety of ways that their peers tackled this problem. One participant described how she broke the shape up into sixteen small equal triangles and and found that the shaded area was 3 of these 16 small triangles.  Another saw that the diagonal from the top left to the bottom right cut the triangle in half.  The large triangle on the bottom is 1/4 and the small triangle in the top left is 1/16.  This made the shaded region 1/2 - 1/4 - 1/16  = 3/16.

We also discussed the likelihood that a student might say that 1/7 of the shape is shaded.  A student might see this a 1 of the 7 pieces of this shape is shaded.  This would be thinking about the number of pieces instead of the area of the pieces and is something they may have done with Tangrams or pattern blocks in earlier grades.

There are lots of questions you can use to extend this discussion. (It might help to label each of the smaller shapes in the square with a letter or hand out a picture of the square for students to work with.)

• How could you shade twice this area (i.e. 3/8 of this square)?
• How many different ways can you find to shade exactly one-quarter of the shape?
• ​If the entire square has an area of 12 square units, what is the area of the shaded section?
• If the shaded section has an area of 6 square units, what is the area of the entire square?

Once everyone was familiar with the idea of creating and describing fractions by shading the square, I handed out a piece of paper to each person (or pairs if you have a big group) that could be folded an hung up on our clothesline number line.  The paper tent had the square and a place to write a fraction on one side and some instructions on the other side.  The instructions were:

1. Shade part of the image below.
2. Find out what fraction of the image you shaded.
3. Record the fraction shaded at the bottom of the image
4. Hang your fraction on the number line in the correct spot.

fraction_number_line.docx
File Size:	21 kb
File Type:	docx

Download File

---

Once everyone had a chance to shade their square and determine their fraction, I had them hang their paper in the appropriate spot on the clothesline.  We determined a few benchmarks: The left end of the clothesline was 0 and the right end was 1.  A spot in the center of the clothesline was 1/2.  The next time I do this activity, I think it might be helpful to create some benchmark cards to hang on the number line.  When participants had different ways of shading the same fraction, we used clothes pins to connect them together on the clothesline to show that they were equivalent. 

After everyone had placed a paper tent on the clothesline, I asked if we had found all of the fractions that could be shaded.  I handed out a few additional blank paper tents and challenged them to find a way to shade a fraction that wasn't already on our clothesline.  As a bit of enrichment, you could ask participants to find a way to calculate or reason how many total fractions are possible with this shape in order to prove if we had found them all or not yet. This was a really fun activity and there was lots of engagement.

EL