|
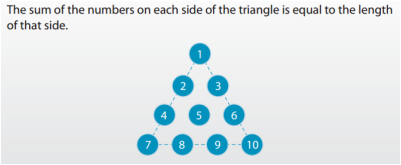
The final chapter of the Math at Work 12 textbook deals with Trigonometry and the Law of Sines and Law of Cosines. Towards the end of the chapter there is a puzzle (p351) that asks students to create a triangle using 9 of the numbers from 1 to 10. Each side of the triangle is the sum of 4 of these numbers. I liked the construct of this puzzle but I wasn't a big fan of the questions that it asked students so I decided to give it an overhaul. An image from the textbook is below.
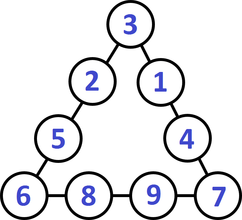
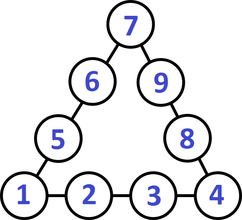
We followed up this warm-up with an open middle style problem using the same situation that would require students to apply the law of cosines. A challenge like the one below gives the students a reason to practice the law of cosines without feeling tedious or repetitive. Directions: Use the numbers 1-9 (using each number no more than once) to fill in the circles. The sum of the numbers on each side of the triangle is equal to the length of that side. What is the triangle with the largest (or smallest) angle that you can make? Hints:
A triangle with the largest angle (there are several variations with the same angle): Side A: 6+8+9+7=30 Side B: 7+4+1+3=15 Side C: 3+2+5+6=16 Angle A: 150.799 Angle B: 14.119 Angle C = 15.082 A triangle with the smallest angle (there are several variations with the same angle): Side A: 1+2+3+4=10 Side B: 4+8+9+7=28 Side C: 1+5+6+7=19 Angle A: 10.844 Angle B: 148.212 Angle C = 20.944
Another challenging question that could be asked is how many different arrangements of the numbers 1 to 9 in the triangle diagram could you make? You have to consider that rotations of the triangle are the same. This would be a challenging combinatorics question even for Pre-calculus 12 students. Nova Scotia Mathematics Curriculum Outcomes Mathematics 11 - G03 Solve problems that involve the cosine law and the sine law, including the ambiguous case. Math at Work 12 - G01 Students will be expected to solve problems by using the sine law and cosine law, excluding the ambiguous case. Math at Work 12 - N01 Students will be expected to analyze puzzles and games that involve logical reasoning, using problem-solving strategies. Mathematics 12 - LR01 Analyze puzzles and games that involve numerical and logical reasoning, using problem-solving strategies Pre-calculus 12 - PC03 Determine the number of combinations of n different elements taken r at a time to solve problems. EL
|
Categories
All
|
||||||||||

 RSS Feed
RSS Feed