Revisiting the Classic Ferris Wheel Problem
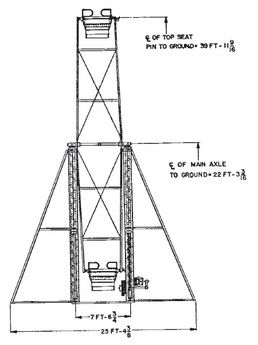
This type of pseudo-context word problem robs students of the opportunity to explore and analyze real-world problems in much depth. Dan Meyer has written quite quite a lot about pseudocontext. My concern with the Ferris wheel problem is not that you can't model the height of a seat on a Ferris wheel with a sine function, it is why would you do it? Instead of doing a textbook problem with a fictional Ferris wheel, I decided to use a real Ferris wheel from a nearby amusement park that some of my students would be familiar with. I visited the park to take a video of the Ferris wheel in action. Below is a 30 second clip of the "Big Ellie" Ferris Wheel at Atlantic Playland. Notice and WonderI started by asking students what they noticed in the video. After brainstorming and recording the students observations I asked students what they wondered about in the video. They asked questions like "how fast is the ride going?", "how tall is this Ferris wheel?", "how far can you see from the top of the ride?", "how long does the ride last?". In order to investigate these questions further we needed to estimate some values such as the radius of the wheel, how long it takes to make one revolution, and the height of the central axis about the ground. I asked students to estimate these values using the clues in the video we watched. We watched it several times in order to get some good estimates. I also talked about some of the mental math required to operate a ride like this. Because it is belt driven, you have to load the Ferris wheel so that it is equally balanced around the wheel. Otherwise, one side of the wheel would become too heavy and the drive cable would slip in the rim and the wheel wouldn't be able to turn! This requires a lot of on the fly estimates of weights of the riders as it is being loaded. In order to get a see how good we did with our estimations we turned to the internet in order to try to hunt down some of these values with a Google search. This lead to a discussion about what keywords we could use to hunt down this information. A search of "height of the central axis of the Ferris wheel at Atlantic Playland" was not very fruitful... an essential skill to solve a problem like this is to translate mathematical language into common terms that you can use for a Google search. Ve Anusic has a great blog post where he discusses a similar problem and the discussion with his students about the information you need and the information you might find online. First we did a search to find Atlantic Playland's website and found that they called their ride "Big Ellie". A search for this name lead us to believe that this Ferris wheel is a No. 5 Big Eli wheel made by Eli Bridge (I later emailed the park and confirmed that this is indeed the model of their Ferris wheel). Eli Bridge's website gave us some interesting information but not exactly what we were looking for. A bit more searching and we were able to find a pdf of the owner's manual for this ride that included a helpful diagram.
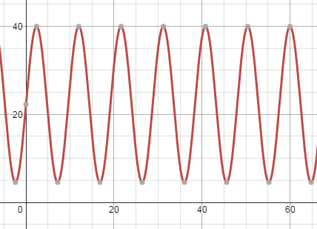
It is only after we were able to answer some of the students' questions regarding the video of the Ferris wheel did we start to talk how we might mathematically modeling the height of a person riding the wheel over time and the periodic nature of this function. Students were much better able to make sense of this visual model once they had a good grasp of the context of the problem.
Nova Scotia Mathematics Curriculum Outcomes Mathematics 12 - RF03 Represent data, using sinusoidal functions, to solve problems. Pre-calculus 12 - T04 Graph and analyze the trigonometric functions sine, cosine and tangent to solve problems. EL
First:
Thank you for your comment Dan. I agree that none of the students’ questions about the Ferris wheel required a trig function to find an answer. None of the questions that I came up with required a trig function either. I did some reflecting on why the Ferris wheel problem seems to be so ubiquitous in mathematics textbooks. I think that it is partially because the Ferris wheel yields such an accurate sinusoidal function. The sine function actually models the real physical motion quite closely... there are not a lot of surprises when going from the real world to the mathematical model. Many other real world contexts used for periodic functions, such as seasonal temperature variations, give estimates based on averages. Also, a Ferris wheel rotates through a complete period of the function quickly so that in just a minute you can watch a number of complete periods. When you’re examining the hours of daylight, you need an entire year to go through a full period. The trouble is, since the Ferris wheel ride is over so quickly, there is not much reason to use a trig equation to make predictions of anything worthwhile. The majority of Ferris wheel questions in textbooks are just that... “textbook questions” that you would only ever see in a textbook. The benefit however of a Ferris wheel question is that you can make an estimate, check/refine your estimate with a video and also see how the trig function accurately models this in reality. Comments are closed.
|
Categories
All
|


 RSS Feed
RSS Feed