|
My wife and I were enjoying a peanut butter cup after dinner a few nights ago. She was eating a standard peanut butter cup (wide and short) and I was eating a miniature peanut butter cup (narrow and tall). I mentioned that the economy rate of mine was higher than hers and therefore my peanut butter cup had a higher peanut butter to chocolate ratio (the economy rate of a container is the ratio of its volume to its surface area. The higher the ratio, the more economical the container is). A 'lively discussion' ensued with a few pauses for the rolling of eyes. Time to break out a ruler, calculator, and the formula for the volume of a frustum (a truncated cone or pyramid) which is the shape of a peanut butter cup. The volume of a frustum is given by the following formula: where R and r are the radii of the top and bottom circles of the truncated cone. The formula can be derived without calculus by taking the entire cone and subtracting the tip to make a frustum. When Heron of Alexandria derived the formula for the volume of a square based frustum, he created the the Heronian mean. The Heronian mean of two numbers A and B is the weighted mean of their arithmetic mean and geometric mean. With this, he was one of the first people to encounter imaginary numbers. The formula below is the general formula for a frustum where A and B are the upper and lower base of the frustum: Lets find the total volume of the big peanut butter cup first. R = 46 mm, r = 38 mm and h = 10 mm. Therefore the volume is 55585.25 mm^3. If we assume that the chocolate is a uniform thickness of 1 mm then we can easily calculate the volume of the peanut butter by subtracting 2 mm from each measurement and recalculating giving 40346.43 mm^3. That means that the volume of chocolate is the difference of these two values or 15238.82 mm^3. This gives us a peanut butter to chocolate ratio of 2.65 Now time to measure the little peanut butter cup. R = 27 mm, r =22 mm and h = 14 mm. Given these measurements, the total volume is 26492.00 mm^3, the volume of peanut butter is 19163.72 mm^3 and the volume of chocolate is 7328.28 mm^3.
This gives us a peanut butter to chocolate ratio for the little peanut butter cup of 2.61. Nearly identical. But the thickness of the chocolate is far from uniform as this cross section shows. The chocolate is actually quite a bit thicker on top and bottom of the little peanut butter cup than on the big one. The peanut butter in the little peanut butter cup actually looks closer to a half-sphere than a frustum. So if you love the chocolate you should eat the little peanut butter cups and if you love the peanut butter, you should eat the big peanut butter cup. EL
Sarah
11/30/2016 12:55:55 am
Ok, but would surface area have any role in the eater's experience of the chocolate? I'm just guessing by looking (which I shouldn't, I know), but it would seem that the bigger peanut butter cup has more tongue-accessible surface area. If, as soon as the candy hits your mouth, you chew it into a homogeneous blob, the amount of chocolate would be uniform throughout, but if you're like most people, you don't eat candy that way. There must be some distinction between flavours/textures, or oreos would be sold as a chocolate mass with a shape most convenient for shipping.
Kelly
9/16/2020 12:14:34 am
I absolutely love this post. Awesome application of mathematics in a fun subject!! Comments are closed.
|
Categories
All
|
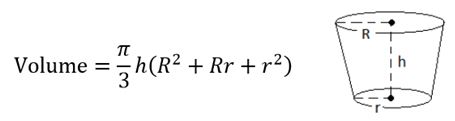
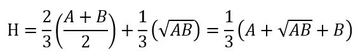


 RSS Feed
RSS Feed