|
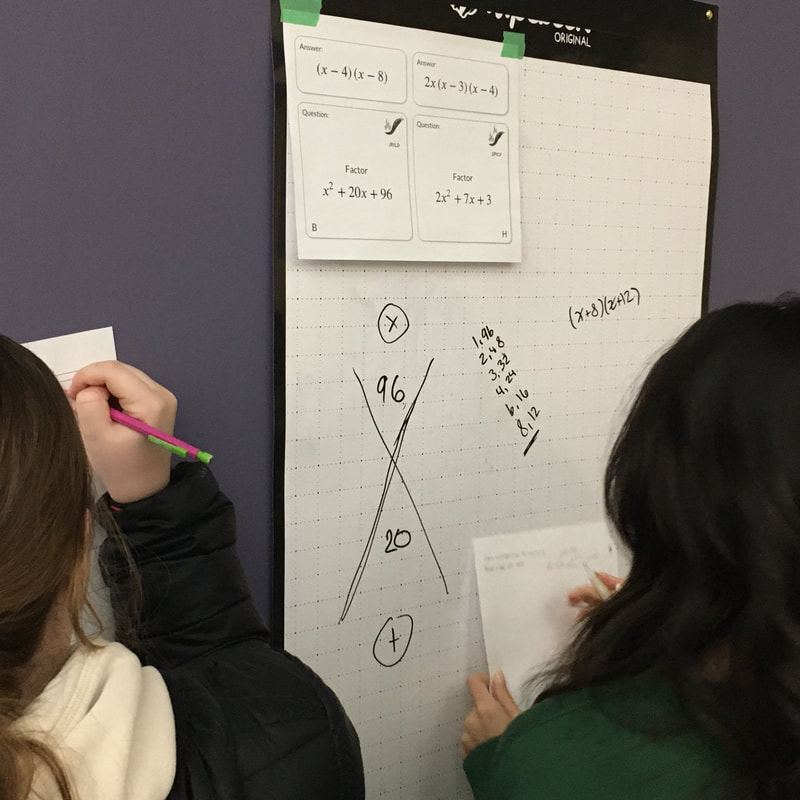
About a week ago, I gave my students a handout to practice multiplying polynomials. It was just a quick check in to practice some of the skills we were learning in class. We were just starting this unit and some students already had some prior knowledge so I decided to give three different levels of challenge to choose from. It was a Friday afternoon last class so I didn't have high expectations for the level of engagement. To my surprise, nearly every student was working diligently on their chosen level of problem. Many students chose the most difficult level. About half chose the "Spicy" questions while the other half chose the "Mild" questions. A couple of students chose the "Medium" level or selected a few questions from several different levels. Letting the students choose their level gave them some agency in their learning. A few students who picked the "Spicy" questions worked hard to master the challenge. They asked lots of questions but felt really good about their accomplishment when they succeeded. I collected these sheets looked through them. I didn't mark them but instead used them to identify and share common misconceptions about factoring. I used examples from the students work (rewriting them in the style of "My Favorite No" from Leah Alcala) as the starting point for the next day's lesson. We discussed what we saw that was wrong but also identified some parts that were on the right track as well. I've been trying out different ways to offer more choice to students. It is important to offer a challenge for students that are ready for it but not to overwhelm students that are still learning. Students in my class come from a number of different feeder schools and have a wide variety of past experience. I created a factoring "scavenger hunt" activity last week for students with two levels of challenge side by side. Students could select the "mild" side if they wanted basic practive or the "spicy" side if they were ready for additional challenge. About 20% of students chose to do the more challenging side. Everyone in the class was very engaged and was able to complete the hunt with instant feedback (if they couldn't find their answer on another sheet, they knew they had made a mistake and worked to correct it). You might also notice letters on each question. I also added a ciphertext message for students to decode when they completed the loop. I've also been including choice in warmup questions and chapter review questions.
Let me know if you have a favourite way to offer students choice in their work and practice. When I first started teaching, reviewing for a test meant one thing. I would stand at the front of the room and reteach each unit, section by section. I would carefully annotate important points and questions that would likely be on the assessment. After reteaching the material, I would hand out a large packet of questions for students to work on. I found that while this helped some students, many students were either bored or confused. If they didn't understand it the first time, hearing me teach it again the same way probably wasn't helping. If they already understood the material then listening to me teach it again was not helping them learn it any better. I recently ran across a couple of blog posts from MathMedic reminding me of why I do things differently now.
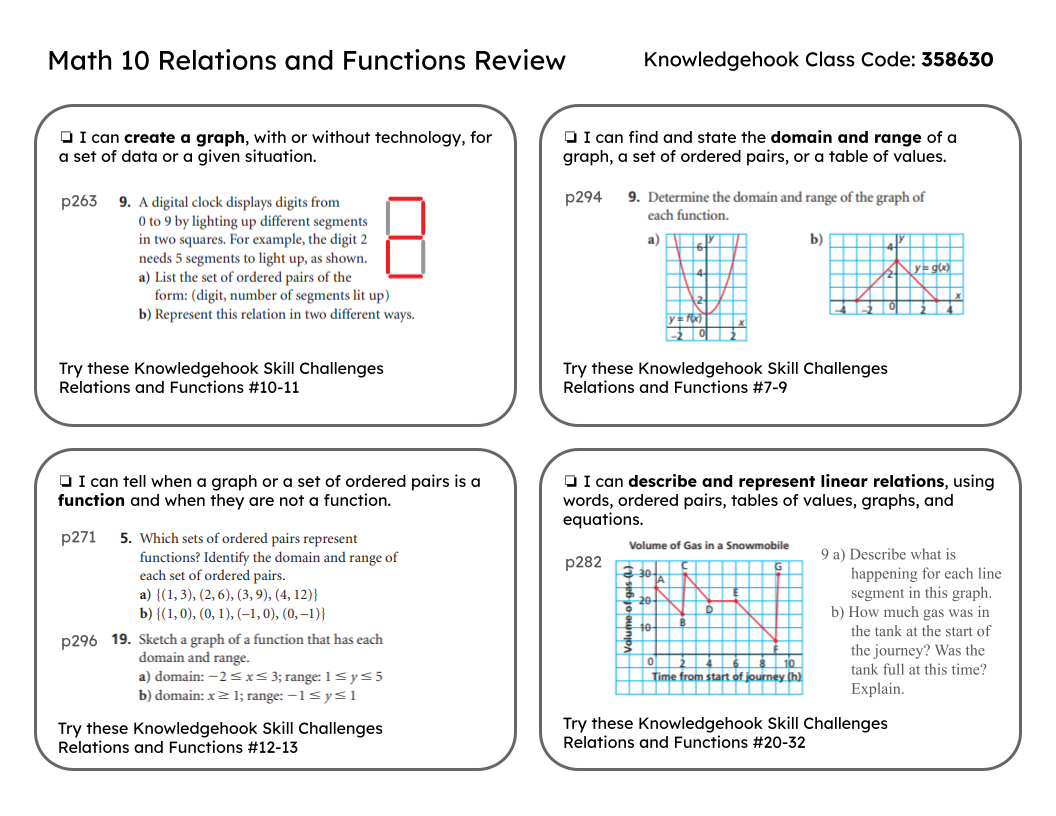
My Mathematics 10 class recently reviewed for a unit test and now we're reviewing for a cumulative assessment on the first half of the course. I typically start with some individual self-assessment where students can review outcomes and identify areas where they need additional practice or review. Next I give students a variety of ways to practice the areas they identified for themselves. Then I like to finish with a (hopefully) fun review game to wrap things ups. Student Self-AssessmentFor our Relations and Functions assessment review, I started with an overview of the outcomes for the unit so students could identify areas where they needed additional support.
Another way we reviewed was to have students in small groups at vertical whiteboards make a list of the most important topics, formula and skills from each unit. This ends up being a study sheet. After groups complete it, they share with the class to see if any groups has something that would benefit everyone. I then collosidated all of these into one class sheet that could be shared on our Google classroom. Individualized ReviewAfter this, I gave them some options to reivew and practice the areas they identified as a challenge. Sometimes this looks like the day in class we practiced domain and range.
Students that want to hear the topic being taught again have lots of options online. There are tons of YouTube channels full of teachers providing lessons on specific topics. I recently found out that a teacher from my school has his own YouTube channel with videos from our curriculum (way to go Mr. Boudreau!). There are also videos on the Nova Scotia Homework Hub, the CEMC Waterloo Courseware site, and many others. Group ReviewTo finish off, I like to play a class game where students work together to study and have some fun while doing it. A game like math basketball is a favourite in my class. We've also done self checking activities like Add 'Em Up or a Scavenger Hunt. Today for the last class of the semester before our assessment, we had a "math market" activity. Students can "buy" questions of different difficulty levels and topics from the market and "sell" solutions back for a profit.
Hopefully students learn lots and find class challenging. I still have lots to learn about teaching and am really trying new things out with my class this year. Let me know if you have a favourite review activity I should know about.
I must admit that I look forward to the beginning of advent and the start of a good advent calendar. All those little doors waiting to be opened. My son and I have a tradition of starting the mornings in December with a Lego advent calendar. This year we have also gotten an electronic games advent calendar from Eight Innovation that looks like it is going to be a lot of fun. Math Advent (or should I say Math-vent?)I also really enjoy exploring online mathematics advent calendar of which I've found several. Here are some of my favourites:
Do you have a favourite advent tradition (mathematical or otherwise)? Let me know about it.
I have an object hanging from my wall at school. Many people don't even notice it or consider why it might be a strange object to see in a building with a firm foundation on dry land. It is a ship's clinometer. A relic of my past days as an officer in the Navy. For me, it serves as a methaphore, a reminder each morning as I walk into the room. Before I became a teacher, I served for seven years as an officer in the Navy. During this time I spent many nights sleeping on board the ship while docked in port as the Command Duty Officer (CDO) while the Commanding Office (CO) was at home. A sort of "in loco parentis" responsibility to literally keep things afloat. Part of this responsibility was to report to the Commanding Officer as he arrived at the ship in the morning. One of the most visible indicators of a ship's health is it's trim. If it is listing to one side or the other you know that something is amiss. I knew that the CO was carefully scrutinizing the trim of the ship as he walked down the pier. If the ship was visibly listing, I knew the CO would want to know what was going on... and it probably wouldn't be a pleasant morning conversation. I have this clinometer on my wall for two reasons. The first is as a reminder to consider, what is really important today? What really needs to get done to keep things on an even keel and what are the things that could wait? What are my true priorities for the day both at work and at home? The second is as a reassurance during stressful times... everything is level and its going to be okay. A bit of self-care to maintain a positive attitude. A reminder to stay positive and find you marigold (if you haven't read this article, I highly recommend you pause now and do so). I guess there is a third reason to have this on my wall... it is a bit of a conversation piece and can spark some interesting discussions. How do you establish your priorities for the day, week or school year? How do you remember to focus your efforts on what you have influence over and let slide the things you have no control of?
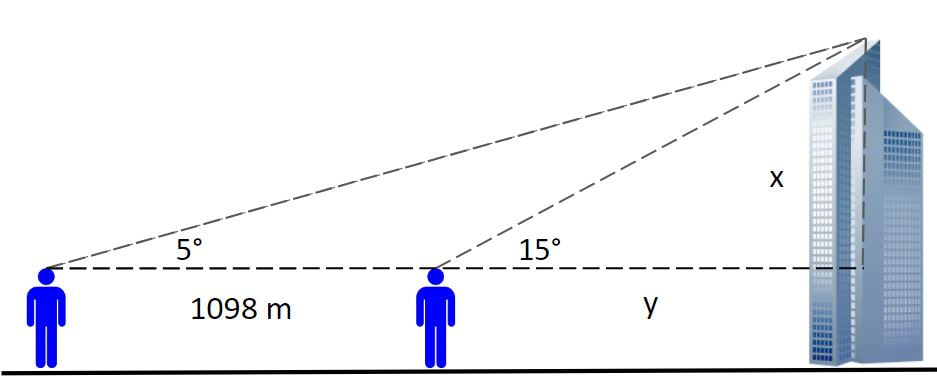
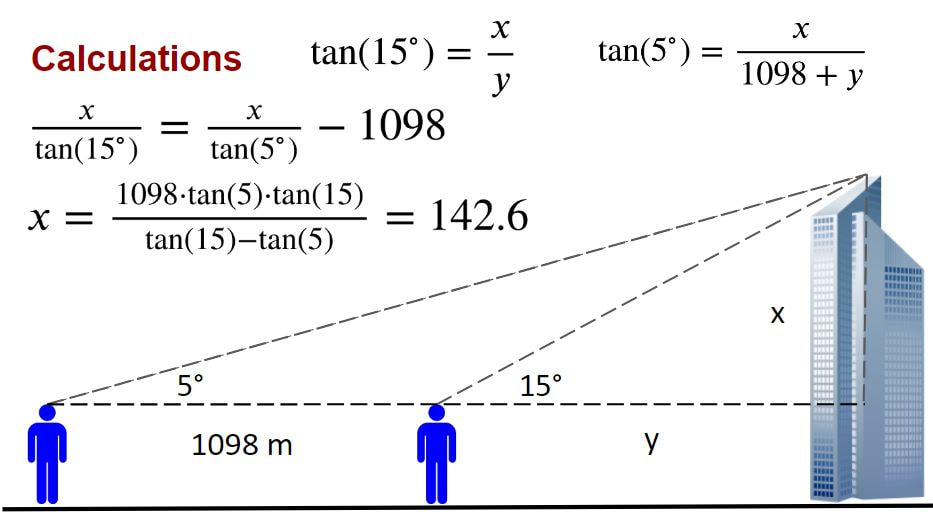
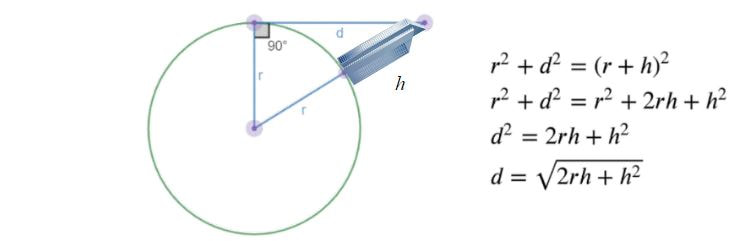
There is a new building going up in my neighborhood. It is so tall, that you can see it from the school I teach at. It makes me curious... how far do you think you could see from the top? As my students are learning about trigonometric ratios, I thought this might be an opportunity to bring the community into the classroom. I asked students to make a prediction about how far they could see given the pictures below. I also let them know that if you stand on the beach, you can see the horizon about 4.8 km away for an average height person (a lot of their initial guesses were even less than this). The first step in satisfiying my curiosity is to collect some data. On my bike ride home, I stopped a couple times to take a picture of the building and to use my Invicta MK1 clinometer to measure the angle of elevation to the top of the building. The first stop was just in front of the school and the clinometer measured about 5 degrees. About a kilometer further down the road, I stopped again for some more pictures and measurements. This time, the angle of elevation to the top of the building was about 15 degrees. I used Google Earth to measure a more precise distance between my two stops. It said that the places where I took the measurement were 1097.98 m apart... lets just call it 1098 m. Now to set up a picture of the situation and include some data. And now for some calculations... At this point, I paused to let the class know that I already knew the height of this building... and my answer was not nearly as accurate as I'd like it to be. I was able to find the building permit online and it says the the building is precisely 103327 cm tall... lets just say 103.3 m. So how did I get so far off? I asked my students to brainstorm some possible sources of error. One is my clinometer. I can only read the angle at an accuracy of about +/- 1 degree... and 1 degree of error at that distance makes quite a big difference in the height. Another source of error is the ground... unlike almost every textbook question, my city is not perfectly flat. Looking at a topological map, I can see that the ground rises about 20 meters over the distance that I took measurements. Not enough to look like you're on a hill but enough to make a difference in my calculations. One final source of error might be that my two measurements were not perfectly in line with the building. I'm not sure how much of a difference this might make but I know it added an additional bit of error. All in all, it was a good conversation about how real life is often not as simple as it looks in the textbook. So back to our question... how far can you see from the top? Well, that is where another right triangle can help. Given the height of the building (103.3 m), the location of the building on a hill (60 m above sea level) plus my height of eye (1.74 m), we can find out how far about sea level the viewpoint is. Since this building has a clear view of the ocean horizon, we can calculate the distance fairly accurately (I figured this part out after listening to an episode of the A Problem Squared podcast). So all these number and calculations tell me that, given the radius of the Earth (about 6371 km) and the height of the view (165.04 m) we have a view distance of 45.9 km. There was much rejoicing by the student who predicted the closest.
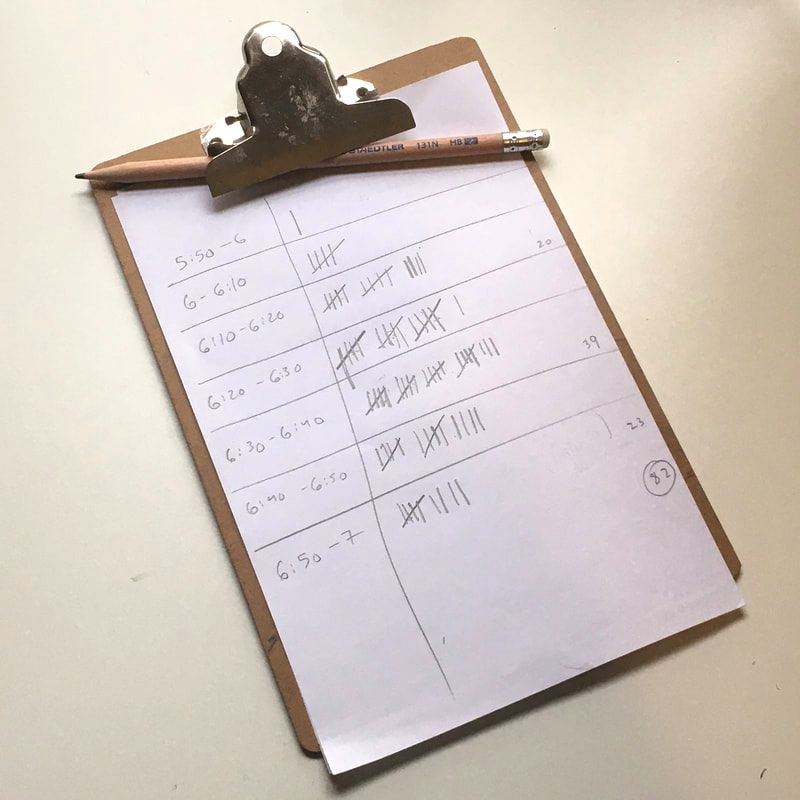
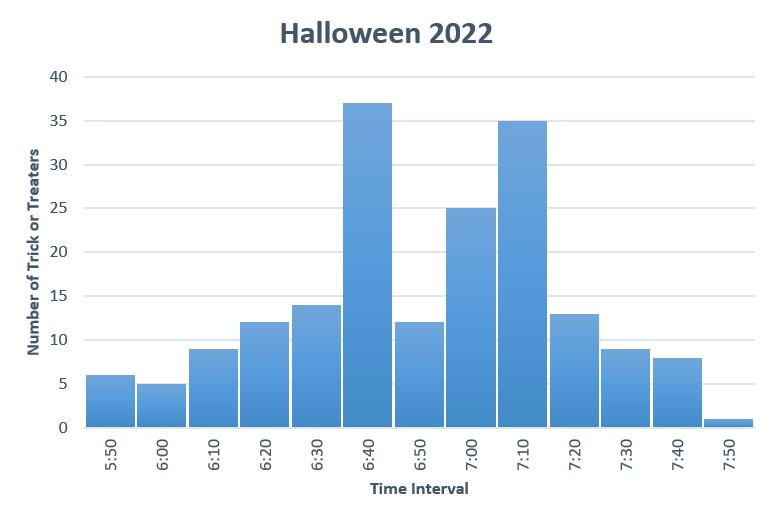
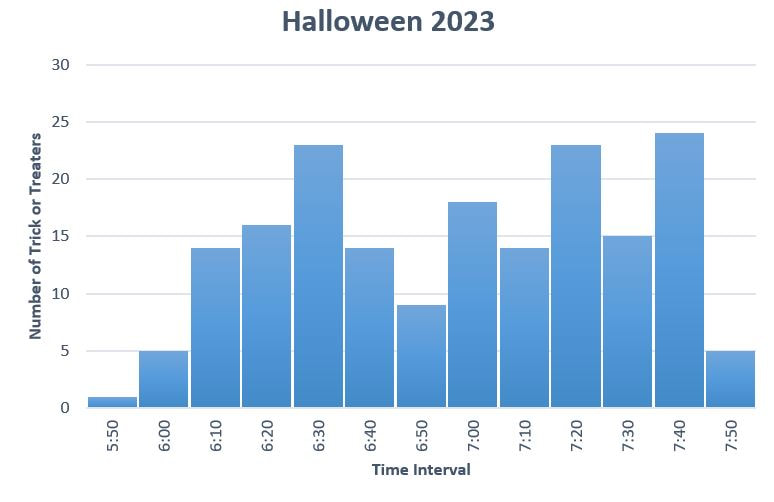
On Halloween morning this year, I showed my Mathematics 10 students my histogram from last year. I asked my class to estimate how many trick-or-treators I had in 2022 based on the image (186) and to predict how many I would get this year. Last year was a beautiful fall night with temperatures of 14°C (57°F) and I had a record number of visitors... this year's weather was still clear but a bit chillier (4°C/39°F). I promised a prize (my leftover candy) to the student with the closest prediction. Students were eager to hear the result in class the next day. It turns out I had 181 trick-or-treators this year and I had two winners. One student guessed 172 and another guessed 190... both were 9 off. Candy was awarded and congratulations offered. Some of my neighbors visited to see how my data collection was going and one neighbor even had their daughter handing out treats and keeping track of their visitors with a hand held tally clicker. Perhaps next year, I can convince some of my students to also keep a tally at their house.
I spent quite a lot of time in various classrooms during the months of May and June. I've noticed a lot of time devoted to in class assessments (aka ICAs). Typically, students are given a page of problems to solve individually with the aid of their notes. In other words and "open notes quiz". These assessments are collected, scored, recorded in the gradebook and then, several days later, returned to students. The written feedback on these assessments are meaningful but take a long time to write and largely ignored by students. There has to be a better way.
I am a fan of self-checking math activities such as Add 'Em Up. In this activity, students solve three or four problems and add the solutions together. They then check this sum with the teacher to see if they are correct. If they are correct, I give the student a stamp and they can move to the next activity. If they are not correct, they can go back to review their work and look for their mistake(s). When they find it, they check their new sum with the teacher. Once they have a correct sum, they got a stamp and continued with the next set of questions. In one classroom, students were used to getting worksheets. Their routine was to complete a worksheet quickly and pass it in. Once they had finished, they were free to relax or look at their phones. When I wouldn't collect the sheet until I had stamped it as all correct they seemed preplexed and annonyed. They weren't used to caring about correctness, just completion. This changed their perspective of the goal of the work... it wasn't about completion and compliance anymore but understanding. Another class was extremely motivated by the stamps. They really liked knowing that the work they turned in was correct. I heard a few comments in the class as I walked around checking work and stamping complete papers. I wrote a few of them down to remember them:
There is a quote attributed to Napoleon Bonaparte, "“Give me enough medals and I’ll win you any war." I feel like stickers and stamps are the classroom equivalent. I was surprised at how much high school students were motivated by these physical marks of success. Like leveling up in their favourite video game, it helped them feel confident and capable. When I was stamping papers, I was using the placement of the stamp to record additional information. If they got the sum correct on the first chance, I would stamp it towards the top right corner. If they needed a few hints and reminder to find their mistakes I would stamp it around the top left corner. If they need lots of support and had some conceptual misunderstandings would stamp it on the bottom half of the page. While I like using self-checking activities with this strategy, you could really do it with any small group of problems or handout. I submitted a proposal to talk about some of these immediate assessment and feedback strategies for the 2023 Northwest Mathematics Conference. I'm hoping my session gets approved. EL
Yesterday I gave a presentation on self-checking math activities for the 2023 NCTM Virtual Conference. I find presenting at conferences valuable because it makes me reflect on my work and think deeply about why I'm selecting or creating certain activities for the classroom. I thought I was finished with my presentation when I saw a variation of a loop card activity that I decided to give a try. Loop cards make for a great self-checking math activity. In a "loop card" activity, the rectangular cards each have two values or expression on them, much like a domino. Students evaluate the expression on the right of side of the card and find a different card whole value on the left side is equivalent. These cards are then joined together (for example, x+3=7 on the right side of one card would join with x = 4 on the left side of another card). Students continue this way until a loop is created with the cards. For a nice example of loop cards, check out Don Steward's post at https://donsteward.blogspot.com/2015/02/loop-cards.html. The variation on this activity that I saw was NRICH's Doughnut Percents activity. In this activity, four students work as a team. Each student is given four cards and tries to make a small loop (for a total of 16 cards). They will typically not have the correct cards and need to trade cards with other members of the group. When complete, there will be four, four-cards loops created, one for each student. The twist with this activity is that the students have to do this quietly. They can just grab cards from other members of the group, but wait for the other student to give them a card that they need. It is very difficult for students to work together silently. I was inspired by this activity to give it a try with other classes. I created a "Derivative Donuts" activity and gave it a try with a Calculus class to review power, product, quotient and chain rules for derivatives. The google slides file can be found here: https://docs.google.com/presentation/d/1lMrJhNWY3jPCqlZrui8EBPe5YeCUdLxt3-akhkGwPxU/edit?usp=sharing. The cards are organized by loop in this file... with a larger group, I would mix the cards up and then have students cut them out... many hands make light work. I used the percent activity above to teach students the rules for the activity using content that they were confident with. Then I gave them the derivative activity which they found challenging. I thought that this activity was a nice change from a typical card sort or question stack type of activity. I like that students worked together as a team to try to create the loops. Because students weren't talking, one student wasn't able to dominate the team and take over the process. Each students had to participate for the group to be successful. The next time I try this activity, I'm going to try having teams of three students with five questions each. I think groups of three might be easier to form small groups (although I'll need more sets of cards). I also recently saw NRICH's Simplifying Doughnut activity which I'm looking forward to try with students. EL
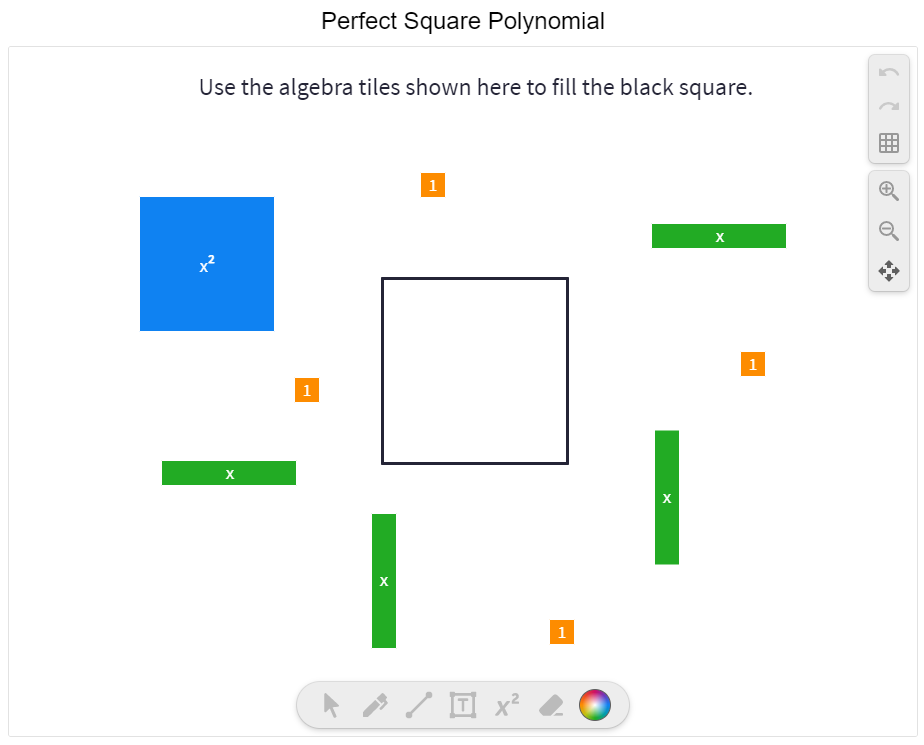
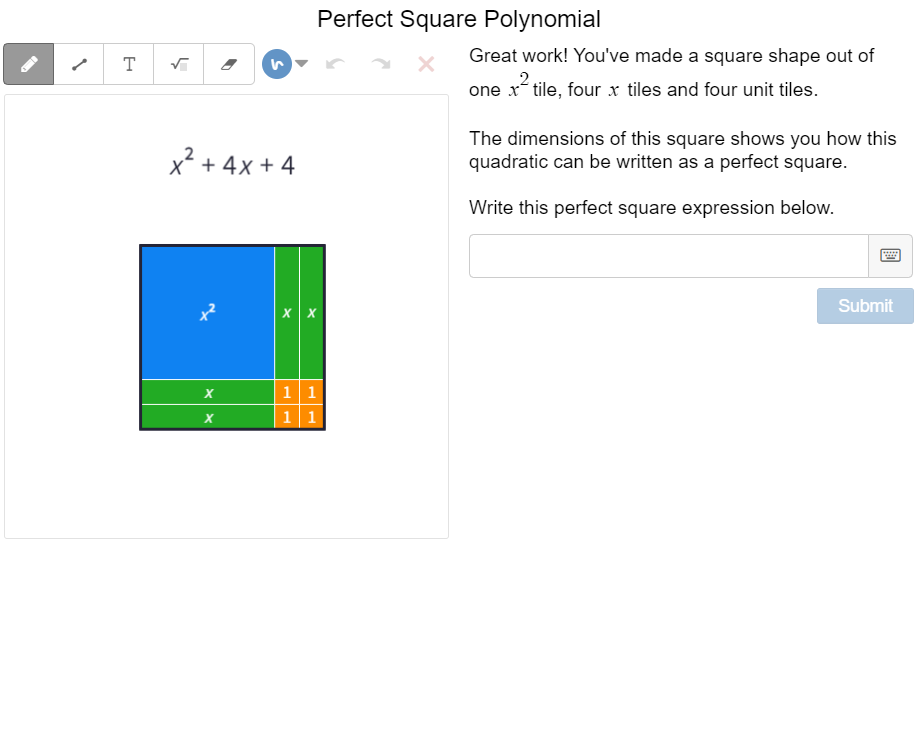
One of my favorite recent technology tools has been the ability to incorporate Mathigon Polypad screens into a Desmos classroom activity. Last week I had the opportunity to work with a high school class learning to change from standard form to vertex form of a quadratic using completing the square. I thought this would be a great opportunity use virtual algebra tiles in a Desmos activity. Students at this school have had lots of experience using physical algebra tiles in previous grades so these students were already familiar with the manipulative. The activity starts out with a review of perfect square numbers and then shows how these relate to perfect square polynomials. Then we moved to using virtual algebra tiles in Polypad to model perfect square polynomials. From there we progressed slowly towards completing the square. Once we built up to generalizing the process of completing the square, students had an opportunity to practice this skill. Instead of giving them feedback on the correctness of their answers, I was able to give them pictures of the algebra tile representation to compare their answers to. I think this helped students reflect on their answers instead of just looking for a green checkmark. I used the pacing tool to make sure most students had finished the question before moving to check their work on the feedback slide. Desmos had an amazing guide to help teachers reflect on the activities they've created. It is called "The Desmos Guide to Building Great (Digital) Math Activities v2.0". I encourage everyone to check it out. Students seemed to enjoy this Desmos activity and the dashboard allowed me to provide targeted support to the few students that appeared to be struggling. After this we did some additional practice and consolidation using a completing the square fill in the blanks sheet from Dr. Austin Maths (a great site for a variety of practice resources). Nova Scotia Mathematics Curriculum Outcomes Precalculus 11 RF04 - Students will be expected to analyze quadratic functions of the form y = ax² + bx + c to identify characteristics of the corresponding graph, including vertex, domain and range, direction of opening, axis of symmetry, x-intercept and y-intercept, and to solve problems.
EL
I was a fan of Mastermind as a kid, envisioning myself like the mysterious gentleman on the box lid, using my superior intellect and logic to solve the puzzle and defeat the codemaker. In this two-player code-breaking board game, the codemaker sets a sequence of four colored pegs using any of six available colors. The codebreaker makes guesses and after each guess, the codemaker responds with key pegs. A black key peg indicates a correct guess in the correct place and a white key peg indicated a correct guess in the wrong place. A quick game with simple rules. Kent Haines, in his blog Games for Young Minds gives some excellent suggestions for questions to ask children when playing a game of Mastermind. He states, "The best question to ask, in my opinion, is 'What did you learn from that guess?' The question is open-ended enough that you aren't guiding your child to a particular conclusion, but it keeps your child focused on the fact that she can learn something from every guess, even one that resulted in no pegs." There are lots of similar guessing games where each incorrect guess gets you closer to the answer. Wordle has become an incredibly popular online word guessing game that has brought new attention to this style of game. There are dozens of versions of similar online guessing games. Dan Meyer wrote about the characteristics of this game in a post titled Why Wordle Works, According to Desmos Lesson Developers. One of the key characteristics is effective feedback. Like a good self-checking task in the mathematics classroom, effective feedback attaches meaning to thinking. Each piece of feedback supports the learner in getting closer to their goal. Pico, Fermi, BagelPico, Fermi, Bagel is a numerical guessing game with a long history. I first learned about this game from the book Math for Smarty Pants by Marilyn Burns (1982). In this book she called the game "Bagels." In this game the codemaker selects a three digit number. After each guess, the codemaker responds with clues. "Fermi" means that there is a correct digit in the correct place. "Pico" means that there is a correct digit in the wrong place. "Bagel" means that the guess has no correct digits. For example, if the code is 967 and the guess is 617, the clue would be "Fermi, pico." Fermi for the 7 (correct digit in the correct place) and pico for the 6 (a correct digit but in the wrong place). A guess of 167 would result in the a clue of "Fermi, fermi". Let me tell you why I like this game...Pico, Fermi, Bagel has been played in classrooms for decades. There is a reason that it has such lasting appeal.
A Pico, Fermi, Bagel Desmos activity
Extension QuestionsHere are some thinking questions you might ask students to consider.
EL
|
Categories
All
|




























 RSS Feed
RSS Feed