|
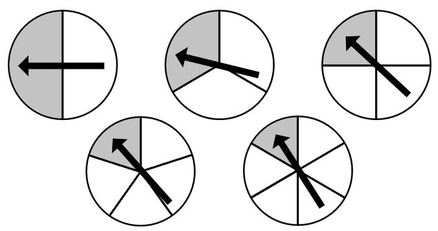
Open middle questions make for great classroom discussions. These are problems that have a closed beginning and end (i.e. an uncomplicated initial question and a single final answer) but an open middle where students can explore different paths and strategies to get to the solutions. Openmiddle.com is a great resource to find these types of questions. Below are a pair of open middle style problems I created for some of the probability outcomes in the NS Mathematics curriculum. Problem #1 - The Spinners Problem Directions: Select three of the spinners below (you may pick more than one of each) such that the total number of sectors in all three spinners totals 10. Select spinners so that the probability of all three spinners landing in the shaded sector is the smallest (or largest). Hint: There are only 4 different ways to select 3 spinners whose sectors add up to 10. In other words, how many ways can you a make a expression with 3 terms that add up to 10 using the numbers 2, 3, 4, 5 or 6. Solution: The four different options for selecting spinners are below. Option 1 yields the greatest probability and option 4 yields the least probability. 1) The greatest probability: 1/2 * 1/2 * 1/6 = 1/24 2) 1/2 * 1/3 * 1/5 = 1/30 3) 1/4 * 1/4 * 1/2 = 1/32 4) The least probability: 1/3 * 1/3 * 1/4 = 1/36 Extension: How would this problem change if you removed the restriction of exactly three spinners? If you could create as many spinners as you wanted such that the sectors totaled to 10 (e.g. 1 spinner with 10 sectors or 5 spinners with 2 sectors, etc.) what would the greatest probability be? 1) The greatest probability: 1/10 = 1/10 2) 1/2 * 1/2 * 1/2 * 1/2 * 1/2 = 1/32 3) 1/5 * 1/5 = 1/25 Problem #2 - The Marbles Problem Directions: "There are _____ red marbles and _____ blue marbles in Bag A. There are _____ red marbles and _____ green marbles in Bag B. " Place a different whole number from 1 to 9 in each blank to make the probability of drawing a red marble from either bag A or B the same. How many different ways can you find to do this? Hint: How can you have a different number of red marbles in each bag but the same probability of selecting a red marble? Solutions: The are 40 different solutions! I first found 5 solutions and then realized that if you just flip the number of red marbles with the other colour, you get another 5 solutions. Then I realized that if you swap the bags, you double the solutions again. I made a Python program to check my work and realized that I had still missed a few and added them in. 1) Bag A: 1 red and 2 blue; Bag B: 3 red and 6 green For each solution below, the following 3 rearrangements are possible. 1B) Bag A: 2 red and 1 blue; Bag B: 6 red and 3 green 1C) Bag A: 3 red and 6 blue; Bag B: 1 red and 2 green 1D) Bag A: 6 red and 3 blue; Bag B: 2 red and 1 green 2) Bag A: 1 red and 2 blue; Bag B: 4 red and 8 green 3) Bag A: 1 red and 3 blue; Bag B: 2 red and 6 green 4) Bag A: 1 red and 4 blue; Bag B: 2 red and 8 green 5) Bag A: 2 red and 3 blue; Bag B: 4 red and 6 green 6) Bag A: 2 red and 3 blue; Bag B: 6 red and 9 green 7) Bag A: 2 red and 4 blue; Bag B: 3 red and 6 green 8) Bag A: 2 red and 6 blue; Bag B: 3 red and 9 green 9) Bag A: 3 red and 4 blue; Bag B: 6 red and 8 green 10) Bag A: 3 red and 6 blue; Bag B: 4 red and 8 green If you want to make this problem a bit easier, just use the numbers from 1 to 6. This gives a total of 16 solutions. These would be 1, 3, 5, and 7 from above plus the 3 additional re-arrangements of each. Extension: Make the number of green marbles a 2 digit number. Nova Scotia Mathematics Curriculum Outcomes Mathematics 7 - SP06 Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events. Mathematics 8 - SP02 Students will be expected to solve problems involving the probability of independent events. Mathematics 10 Essentials - G1 Express probabilities of simple events as the number of favourable outcomes divided by the total number of outcomes Mathematics 12 - P03 Solve problems that involve the probability of two events. EL
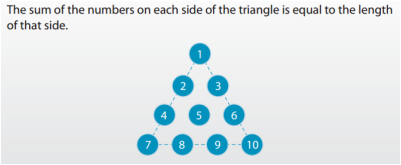
The final chapter of the Math at Work 12 textbook deals with Trigonometry and the Law of Sines and Law of Cosines. Towards the end of the chapter there is a puzzle (p351) that asks students to create a triangle using 9 of the numbers from 1 to 10. Each side of the triangle is the sum of 4 of these numbers. I liked the construct of this puzzle but I wasn't a big fan of the questions that it asked students so I decided to give it an overhaul. An image from the textbook is below.
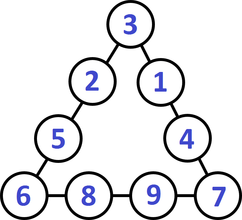
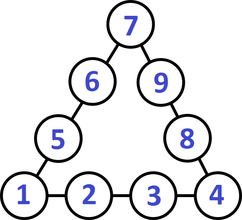
We followed up this warm-up with an open middle style problem using the same situation that would require students to apply the law of cosines. A challenge like the one below gives the students a reason to practice the law of cosines without feeling tedious or repetitive. Directions: Use the numbers 1-9 (using each number no more than once) to fill in the circles. The sum of the numbers on each side of the triangle is equal to the length of that side. What is the triangle with the largest (or smallest) angle that you can make? Hints:
A triangle with the largest angle (there are several variations with the same angle): Side A: 6+8+9+7=30 Side B: 7+4+1+3=15 Side C: 3+2+5+6=16 Angle A: 150.799 Angle B: 14.119 Angle C = 15.082 A triangle with the smallest angle (there are several variations with the same angle): Side A: 1+2+3+4=10 Side B: 4+8+9+7=28 Side C: 1+5+6+7=19 Angle A: 10.844 Angle B: 148.212 Angle C = 20.944
Another challenging question that could be asked is how many different arrangements of the numbers 1 to 9 in the triangle diagram could you make? You have to consider that rotations of the triangle are the same. This would be a challenging combinatorics question even for Pre-calculus 12 students. Nova Scotia Mathematics Curriculum Outcomes Mathematics 11 - G03 Solve problems that involve the cosine law and the sine law, including the ambiguous case. Math at Work 12 - G01 Students will be expected to solve problems by using the sine law and cosine law, excluding the ambiguous case. Math at Work 12 - N01 Students will be expected to analyze puzzles and games that involve logical reasoning, using problem-solving strategies. Mathematics 12 - LR01 Analyze puzzles and games that involve numerical and logical reasoning, using problem-solving strategies Pre-calculus 12 - PC03 Determine the number of combinations of n different elements taken r at a time to solve problems. EL
I really like some of the questions found on the Openmiddle.com website. It is a great resource for questions that really get students thinking. They are often formatted so that there is a very low threshold for entry to the problem but they allow for enrichment and extensions. I created the problem below for a professional development session for Math 10 teachers. Students in the Math 10 course are near the following outcome in the yearly plan: AN03 Students will be expected to demonstrate an understanding of powers with integral and rational exponents. Fill in the boxes with whole numbers 1 through 6, using each number at most once, so that the value of the expression is as large (or as small) as possible.
In order to verify that these were correct values, I wrote a short program in Python (see below) to check all of the 720 possible (6!) values. It was my personal Hour of Code activity. I`m just learning to use Python so my code could definitely be more efficient. If you can write some better code, let me know and I`ll post it here and give you credit. ValuesList=[1.0,2.0,3.0,4.0,5.0,6.0] largest = 0 smallest = 10000 for i in ValuesList: for j in ValuesList: for k in ValuesList: for l in ValuesList: for m in ValuesList: for n in ValuesList: if i!=j and i!=k and i!=l and i!=m and i!=n and j!=k and j!=l and j!=m and j!=n and k!=l and k!=m and k!=n and l!=m and l!=n and m!=n: z=((i/j)**k)*(l**(m/n)) if z > largest: largest = z print "Largest",largest,i,j,k,l,m,n if z < smallest: smallest = z print "Smallest",smallest,i,j,k,l,m,n Update: I submitted this problem to the OpenMiddle.com website and it has been posted there. EL
|
Categories
All
|
||||||||||||

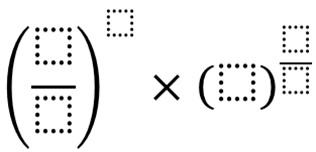
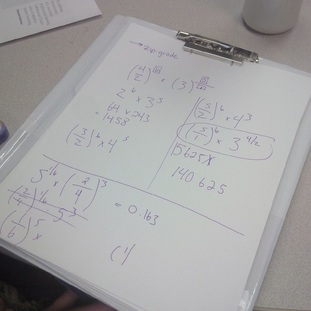
 RSS Feed
RSS Feed