|
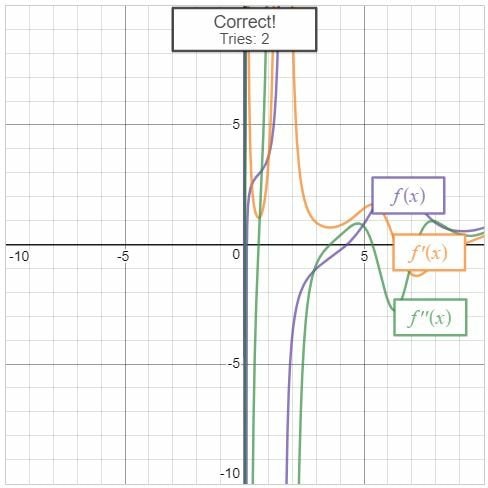
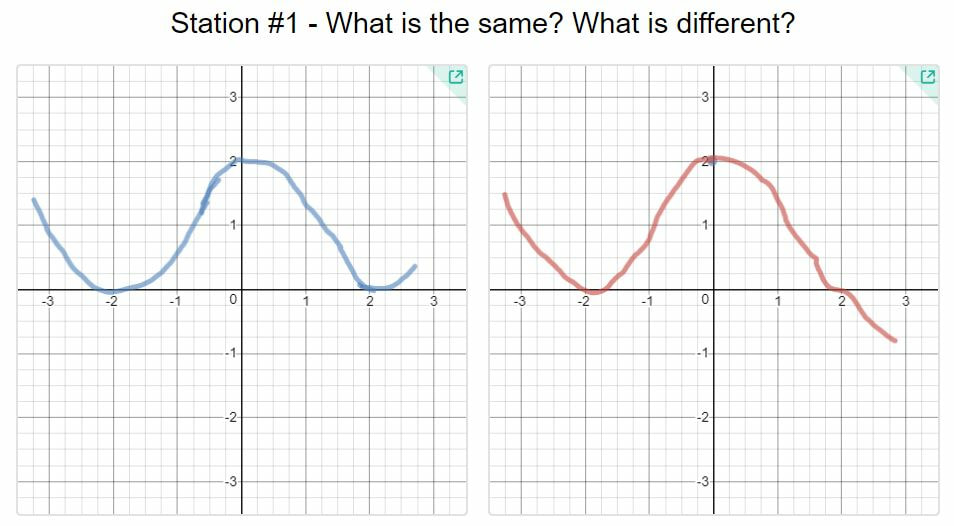
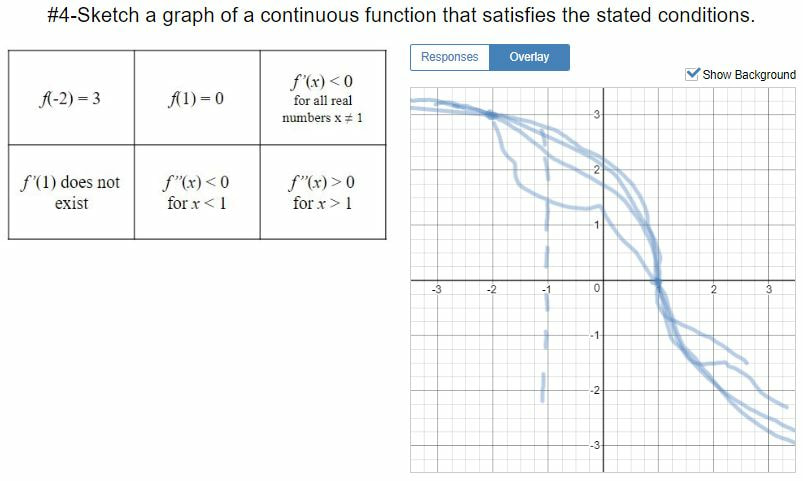
I recently had the opportunity to work with a calculus class on curve sketching and how derivatives affect the shape of a graph. The classroom teacher and I brainstormed some ideas about how we might infuse some hands on activity into the lesson. We decided to try an activity called Functions on the Floor. I originally saw an outline of this activity in a presentation from Liana Dawson called Hands-On Calculus Activities. Warm up - Functions and Their DerivativesWe started the class out with a Demos activity called Functions and Their Derivatives. We had students work in pairs on this activity. In the first part of the activity, students are presented with the graphs of three functions and they have to decide which is the original function, which is the derivative and which is the second derivative. In the second part of the activity, students create their own challenge and then get an opportunity to try out the challenges created by other groups. I really like the collaboration and discussions creating by working on these challenges. Functions on the Floor InstructionsAfter the warm up, we transitioned to the Functions on the Floor activity. We used masking tape to create several coordinate systems on the floor with the x- and y-axis labeled from -3 to 3. At each of these stations was a list of information about a continuous function. Students used a small rope to create a function on the axis that satisfied all of the conditions listed. They then drew their function into a Desmos activity I had prepared. Using the drawings in the Desmos activity we could monitor students activity and plan for our review of the functions at the end of class. We heard some really constructive conversations taking place. The Google slides for the stations can be found here. Sharing our WorkI thought that this activity was a nice way to incorporate both hands-on physical problem solving while still leveraging some of the power of online tools like Desmos. I learned a few lessons doing this activity and the classroom teacher and I had a productive discussion after the lesson. We talked about how the lesson went and where we saw areas for improvement. We both agreed that eight stations was more than needed as it took some time for the discussions in the student groups to come up with a reasonable graph. We thought that some of the stations could have fewer constraints to consider as well. Also, I think next time I would use something besides rope. I had pretty inexpensive rope and it wasn't as pliable as I would have liked. I think a thick piece of yarn might have worked just a well. If you give this activity a try, let me know how it goes. Nova Scotia Mathematics Curriculum Outcomes Calculus 12 B15 - Demonstrate an understanding of critical points and absolute extreme values of a function Calculus 12 B16 - Find the intervals on which a function is increasing or decreasing Calculus 12 C5 - Apply the First and Second Derivative Tests to determine the local extreme values of a function Calculus 12 C6 - Determine the concavity of a function and locate the points of inflection by analyzing the second derivative EL
Comments are closed.
|
Categories
All
|





 RSS Feed
RSS Feed