|
Over the recent holiday weekend, I brought out my copy of Dice Games Properly Explained by Reiner Knizia (@ReinerKnizia). I enjoy playing dice games at home with my family as well as playing dice games in class with students. Dice games often have simple rules and typically don't require of lot of material other than dice. Dice are a great mathematics manipulative that can be used with wide range of ages. Even very young students can practice subitizing numbers from 1 to 6 by reading the dots on the face of the dice. Below are a few of my favourite mathy dice games. Shut the Box
The object of the game is to cover as many of the 9 boxes as possible. Any numbers left uncovered at the end of your turn are added together. "Shutting the box", or covering all the numbers, leads to a perfect score of 0. The player with the lowest score is the winner. On the players turn, they roll the dice and add them together. You can then cover any boxes that are not already shut that sum to the total you rolled. For example, if I rolled a 2 and 4 my total is 6. I could cover the 6 box, the 5 and 1, the 4 and 2 or the 1, 2 and 3 boxes if they are uncovered. If I can't partition my number to cover any boxes then my turn is over and I add up any uncovered boxes to determine my score. This is a fun game with some strategy to it. It really focuses on early addition skills as well as partitioning numbers in a variety of way. It is a great game for a lower elementary classroom. NS Outcomes: Primary - N04 Students will be expected to represent and describe numbers 2 to 10 in two parts, concretely and pictorially. Mathematics 1 - N04 Students will be expected to represent and partition numbers to 20. Mathematics 2 - N10 Students will be expected to apply mental mathematics strategies to quickly recall basic addition facts to 18 and determine related subtraction facts. Even Minus OddIn this game, players take turns throwing six dice. You then total all the even dice together and all the odd dice together. Subtract the odd total from the even total to get your score. Take counters from the centre of the table equal to your score. If you have a negative total, pay that number of counters to the centre (don't worry, if you don't have any counters left, you're still in the game). When all the counters are gone from the centre, the game is over and the player with the most counters wins. Start with about 10 counters in the centre or more if you have a large group playing. NS Outcomes: Mathematics 2 - N02 Students will be expected to demonstrate if a number (up to 100) is even or odd. Mathematics 2 - N10 Students will be expected to apply mental mathematics strategies to quickly recall basic addition facts to 18 and determine related subtraction facts. Game of SixIn this category game, you need only one die and a score sheet. Players take turns rolling the die over six rounds. One your turn, roll the die and decide which category to score. Multiply the number on your die by the category value (1, 2, 3, 4, 5 or 6). Each category can be used only once each game. For example, if you roll a six on your first turn, you could score it in category 6 and earn 6x6 = 36 points. At the end of the six rounds, each player adds up their total points. The player with the most points wins. NS Outcomes: Mathematics 4 - N05 Students will be expected to describe and apply mental mathematics strategies, to recall basic multiplication facts to 9 × 9, and to determine related division facts. Mathematics 5 - N03 Students will be expected to describe and apply mental mathematics strategies and number properties to recall, with fluency, answers for basic multiplication facts to 81 and related division facts. Ninety-NineThe focus of this game is on the order of operations for whole numbers. Five dice are rolled in this game and the player who rolls the dice calls out any number they wish between 33 and 99. This is the target number for the round. Once the dice are rolled, players create an expression using all five numbers on the dice and any operations (+, - , x, ÷). The goal is to create an expression whose value is as close as possible to the target number without going over. Divisions must work out without a remainder. Players secretly write down their expression. Once everyone has an expression (or a reasonable amount of time has passed), players reveal their expression. The player closest to the target scores a zero. All other players score the difference between their expression's value and the values that was closest (to a maximum of 5). Play as many rounds as their are players so each person can have a round setting the target. NS Outcomes: Mathematics 5 - N03 Students will be expected to describe and apply mental mathematics strategies and number properties to recall, with fluency, answers for basic multiplication facts to 81 and related division facts. Mathematics 6 - N09 Students will be expected to explain and apply the order of operations, excluding exponents, with and without technology (limited to whole numbers). A Focus on Mathematical ContentThere are lots of really fun dice games in Reiner's book although some are more suited to a mathematics classroom than others. I also really like the chapter on the theory of dice and probability (chapter 3). I think the games above are not only fun, but closely related to mathematics outcomes. A recent post I read from Hilary Kreisberg (@Dr_Kreisberg) discussed a protocol to assess good classroom tasks. One dimension of her protocol was to assess the mathematical content of a task and ask yourself if the task aligns well with specific grade-level standards. I think this is an important aspect to remember and not just play games that are fun, but ones that also offer meaningful mathematical practice. EL
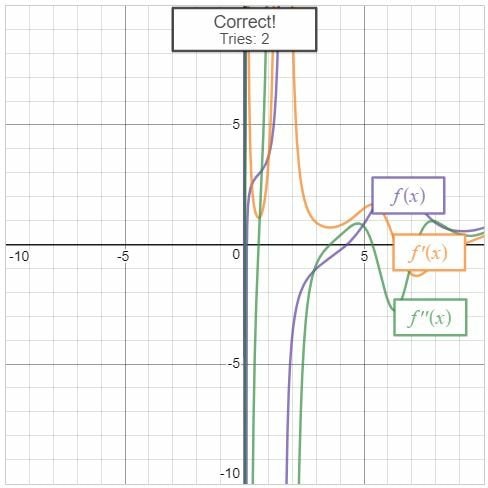
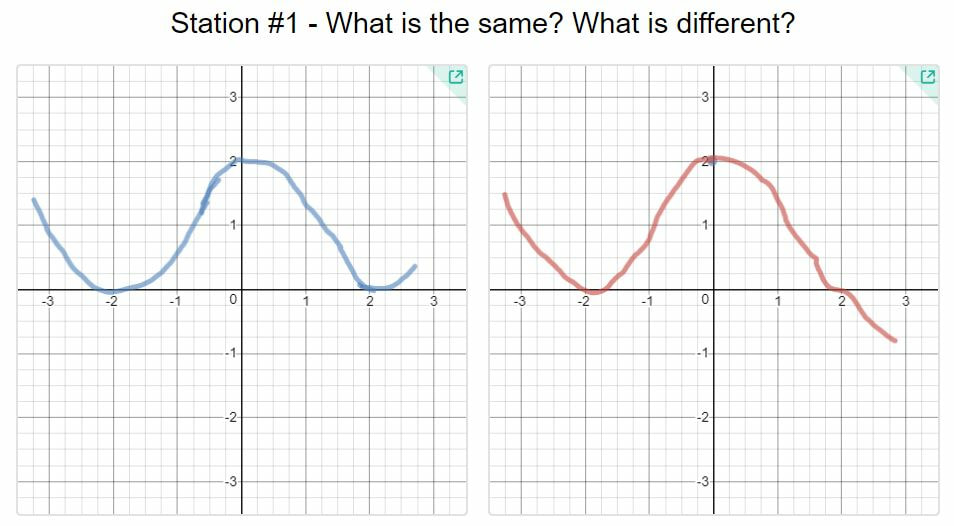
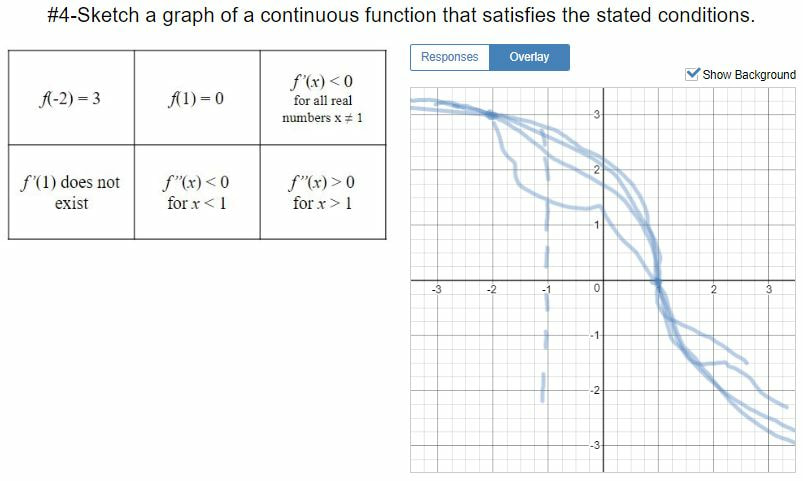
I recently had the opportunity to work with a calculus class on curve sketching and how derivatives affect the shape of a graph. The classroom teacher and I brainstormed some ideas about how we might infuse some hands on activity into the lesson. We decided to try an activity called Functions on the Floor. I originally saw an outline of this activity in a presentation from Liana Dawson called Hands-On Calculus Activities. Warm up - Functions and Their DerivativesWe started the class out with a Demos activity called Functions and Their Derivatives. We had students work in pairs on this activity. In the first part of the activity, students are presented with the graphs of three functions and they have to decide which is the original function, which is the derivative and which is the second derivative. In the second part of the activity, students create their own challenge and then get an opportunity to try out the challenges created by other groups. I really like the collaboration and discussions creating by working on these challenges. Functions on the Floor InstructionsAfter the warm up, we transitioned to the Functions on the Floor activity. We used masking tape to create several coordinate systems on the floor with the x- and y-axis labeled from -3 to 3. At each of these stations was a list of information about a continuous function. Students used a small rope to create a function on the axis that satisfied all of the conditions listed. They then drew their function into a Desmos activity I had prepared. Using the drawings in the Desmos activity we could monitor students activity and plan for our review of the functions at the end of class. We heard some really constructive conversations taking place. The Google slides for the stations can be found here. Sharing our WorkI thought that this activity was a nice way to incorporate both hands-on physical problem solving while still leveraging some of the power of online tools like Desmos. I learned a few lessons doing this activity and the classroom teacher and I had a productive discussion after the lesson. We talked about how the lesson went and where we saw areas for improvement. We both agreed that eight stations was more than needed as it took some time for the discussions in the student groups to come up with a reasonable graph. We thought that some of the stations could have fewer constraints to consider as well. Also, I think next time I would use something besides rope. I had pretty inexpensive rope and it wasn't as pliable as I would have liked. I think a thick piece of yarn might have worked just a well. If you give this activity a try, let me know how it goes. Nova Scotia Mathematics Curriculum Outcomes Calculus 12 B15 - Demonstrate an understanding of critical points and absolute extreme values of a function Calculus 12 B16 - Find the intervals on which a function is increasing or decreasing Calculus 12 C5 - Apply the First and Second Derivative Tests to determine the local extreme values of a function Calculus 12 C6 - Determine the concavity of a function and locate the points of inflection by analyzing the second derivative EL
We started the lesson by reviewing strategies for decimal division. To create a need for division we had an activity where students found an average. We used the Estimating Time activity from NRICH. We challenged several student volunteers to estimate 5 seconds, giving each student three tries. We then asked the class to find the average of each student by dividing the total of their three attempts by three (just a note that students don't have a formal introduction to mean, median and mode until grade 7 SP01). After students finished, we highlighted several strategies that we saw student using and had the students explain their division strategies. We saw students making equal groups with base 10 blocks, partial quotients and the standard long division algorithm. Check out Graham Fletcher's progression of division video for some background on division strategies. Designing a Spinning Top
Testing DesignsGroups used a stopwatch (on their phone app or on https://stopwatch.onlineclock.net/ using a Chromebook) to see how long each top would spin. The tested each design three times and recorded their times. They then used division to find the average spin time for each design. They used this data to decide which of their designs was the best. Sharing DesignsAt then end of the class we led a class discussion about their design process. We asked students what characteristics made a top spin longest: size of the top (number of cubes used), shape of the top (symmetry). How it was spun seemed to be a big factor. One student spun the top from the sides instead of the top and was able to get a long spin (average of about 25 seconds). Further PracticeNova Scotia Mathematics Curriculum Outcomes Mathematics 6 N08 - Students will be expected to demonstrate an understanding of multiplication and division of decimals (one-digit whole number multipliers and one-digit natural number divisors). Mathematics 6 SP02 - Students will be expected to select, justify, and use appropriate methods of collecting data, including questionnaires, experiments, databases, and electronic media. Mathematics 7 N02 - Students will be expected to demonstrate an understanding of the addition, subtraction, multiplication and division of decimals to solve problems (for more than one-digit divisors or more than two-digit multipliers, the use of technology is expected). Mathematics 7 SP01 - Students will be expected to demonstrate an understanding of central tendency and range by: determining the measures of central tendency (mean, median, mode) and range; determining the most appropriate measures of central tendency to report findings. EL
|
Categories
All
|











 RSS Feed
RSS Feed