|
There are some really big doors around Halifax. The door on Irving Shipbuilding's Halifax Shipyard Assembly and Ultra Hall facility is big enough for large "mega-blocks" of ships under construction to pass through. The doors at IMP Aerospace's Hangar #9 at the Stanfield International airport is big enough for large aircraft to pass through. Which door do you think is the largest? What Do You Mean by Largest?The first thing you might want to do is settle on what you mean by "largest". Do you mean width, height, area, mass or some other measurement? Each of these doors might be the largest for a specific measurement. For example, the aircraft hangar door is made of metal and quite probably has more mass than the shipyard door which is constructed of a polyester fabric. Estimating DimensionsThe shipyard door is really tall but the aircraft hangar door is really wide. Below are pictures of the two facilities from Google earth with the same scale so that you can compare the buildings that these doors are on. https://www.google.ca/maps/@44.6674497,-63.5972041,542m/data=!3m1!1e3 https://www.google.ca/maps/@44.8701869,-63.5322158,573m/data=!3m1!1e3 Door Dimensions and Surface Area
So the shipyard door has the largest height and the largest area but the hangar door has the largest width and the largest mass. Would you call this a tie? How would you determine the winner?
More Big DoorsDo you know of other big doors around Halifax? Have you seen bigger doors in other parts of Nova Scotia or the rest of Canada? What is your definition of door? Note of Thanks: I want to say thank you to the people at both Irving Shipyard and IMP Aerospace who were very helpful providing information for this post. EL
This is the second year for the Math Photo Challenge on twitter. Each week a new challenge topic is presented. During the challenge, you can follow @mathphoto16 on twitter to see the weekly prompt. You can also visit https://mathphoto16.wordpress.com/challenges/ to see the weekly prompt. Participants post photos on twitter and use the hashtag #mathphoto16 and the hashtag for the weekly prompt. This year, the challenge is being hosted and organized by Amie Albrecht (@nomad_penguin) and John Rowe (@MrJohnRowe) from Australia. Last year, I sat back and watched as people tweeted photos but this year I decided to participate and encouraging other teachers and students to do so as well. With this post, I'm going to recap the challenges and the photos I tweeted throughout the summer.
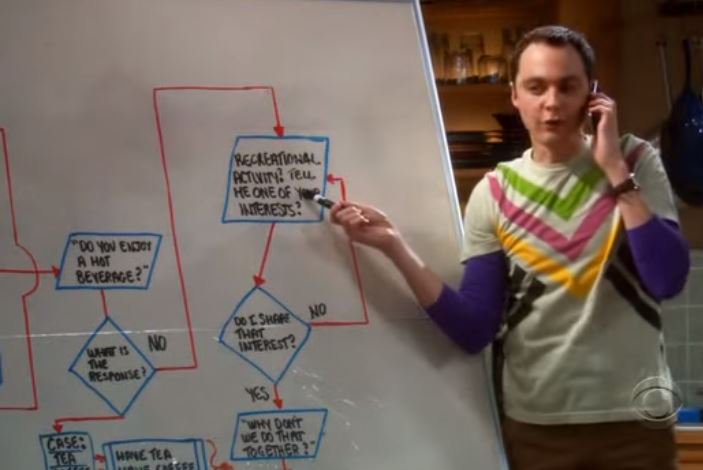
The Week #2 (June 19 - 25) challenge was #scale. Scale is a ratio that measures the relative size of two objects. We encounter scale in our daily lives such as longer/shorter, faster/slower and bigger/smaller. I posted two photos from the Halifax Stanfield International Airport baggage carousels. Each of the three baggage carousels in the domestic arrivals area has a scale model built by Anchor Models. The MacKay and Macdonald Bridge models are 47 ft long and have a scale of 1/60. The model of the Halifax Town Clock has a scale of 1/12. The Week #3 (June 26 - July 2) challenge was #lines, curves and spirals. I posted a photo of a pediment portico and eyebrow dormer from a house in the South End of Halifax. I really like this style of architecture and it is pretty common on the peninsula in Halifax. A few weeks later, I was at the Halifax Central Library and took a photo of the lines and shadows in the buildings central atrium. The Week #4 (July 3 - 9) challenge was #multiples. Many objects can be arranged in multiples and groups. This helps us count them more easily and share them out equally. I posted two photos for week 4. The first is an arrangement of tea cups from a tea house in Beijing. The second is a picture of the 3 chimneys from the Tufts Cove Generating Station on the Halifax Harbour. I like how each of the 500 ft tall smokestacks are partitioned into alternating white and red bands. The Week #5 (July 10 - 16) challenge was #zero. Without zero, mathematics would be nothing. Search out the concept of zero. Be creative in your interpretation. I posted a photo of the sign for Exit 0 on Nova Scotia Highway 102. While most Canadian provinces use kilometre based exit numbers, Nova Scotia uses sequential exit numbers. The only other Canadian province which uses sequential exit numbers is Newfoundland and Labrador. The Week #6 (July 17-23) challenge was #infinity. Infinity characterizes things that never end. Look for interpretations of infinity. This was a difficult concept to capture with a photo and there were relatively few photos submitted on Twitter. I posted two photos. The first depicted how the imagination is infinite. A toy such as a set of blocks can be used for an limitless number of different games and activities. The second photo I posted was from the television show The Big Bang Theory. In the episode titled "The Friendship Algorithm" (S2, E13), Sheldon gets stuck in an infinite loop in his algorithm. The Week #7 (July 24-30) challenge was #shapes. Shapes enclose the space around us into areas, in both regular and irregular ways. Along with single shapes, look for congruence, similarity, tessellations and more. I posted a photo that I took of the The Beijing National Aquatics Center. The bubble like geometric shapes covering the exterior of the building are based on the Weaire–Phelan structure. I really enjoyed participating in this photo project and seeing all of the interesting and creative photos that were posted by people from all around the world. It gave me a purpose to view my community through a mathematical lens and connect mathematical ideas to the world around me. EL
The Sno Cap Drive In in Sisters, Oregon is a diner that serves homemade ice cream and old fashioned burgers. The food here is great and the homemade ice cream is delicious. I stopped in this summer for a scoop of Cookie Monster ice cream. While waiting in line, I had some time to notice and wonder about the prices listed on the menu. What is going on here? NoticingI noticed the differences in price between having your burger with potato chips or with french fries. Depending on the burger you're having, it costs anywhere from 45¢ to 95¢ more to have fries instead of chips. I also noticed the difference between the burgers with cheese and those without cheese. To add cheese to your deluxe burger is an additional 80¢ but to add cheese to your bacon burger is only an additional 30¢. WonderingIs there a pattern or rule to the price differences between having a burger with chips or fries? The list of differences between chips and fries is: 70¢, 70¢, 65¢, 60¢, 45¢, 80¢, 75¢, 75¢, 95¢, 70¢, 65¢, 70¢, 70¢, 65¢, 80¢, 60¢. The values range from a minimum of 45¢ to a maximum of 95¢. The mean difference is 70¢ and the standard deviation (a measure of variation) is 11¢. I tried sorting the burgers in a variety of ways but there appears to be no pattern to the difference in price between chips and fries. This restaurant is in Oregon, which has no sales tax (one of only five such states), so the prices are not set so that when tax is applied, the total is a round number. I'm assuming that every burger gets the same amount of fries, but perhaps this isn't the case. I wonder if they get many questions about this? If you wanted to give the prices on this menu an overhaul, how would you price these burgers, chips and fries? Could you come up with a more logical system of pricing? What factors would go into making these price decisions? Which burger do you think is currently the most profitable based on the current prices? Nova Scotia Mathematics Curriculum Outcomes Grade 7 SP01 - Students will be expected to demonstrate an understanding of central tendency and range by: determining the measures of central tendency (mean, median, mode) and range; determining the most appropriate measures of central tendency to report findings. Grade 7 N02 - Students will be expected to demonstrate an understanding of the addition, subtraction, multiplication and division of decimals to solve problems (for more than one-digit divisors or more than two-digit multipliers, the use of technology is expected). Mathematics 11 S01 - Demonstrate an understanding of normal distribution, including: standard deviation and z-scores. EL
|
Categories
All
|
||||||||||||















 RSS Feed
RSS Feed