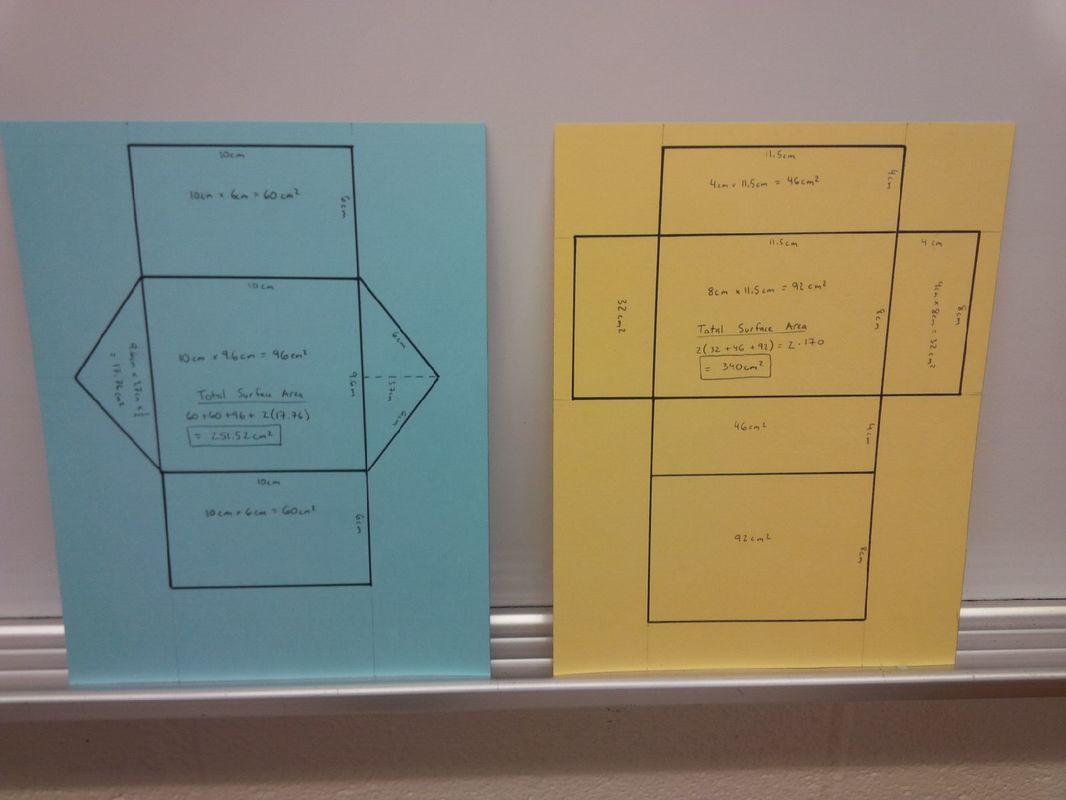
Constructing Rectangular and Triangular PrismsDetermining the surface area of a prism can get a bit stale. Textbooks contain lots of pictures of various right rectangular and triangular prisms. These prisms are carefully labeled with the exact information that a student needs. Students are given the task of inserting these numbers into a formula and doing some basic calculations. These types of problems often don't require much thought. I've recently had the pleasure of working in some junior high classrooms. We were looking for a more hands-on and thought provoking activity for surface area. We were also looking for an activity in which students could be creative. This is what we came up with. Students, working in pairs, are given either a yellow or blue piece of coverstock. Students with a yellow piece are asked to design and draw the net of a right rectangular prism. Students with a blue piece are asked to design and draw the net of a right triangular prism. Students can draw whatever size or shape prism they wish as long as it covers the majority of the paper (at least half). Students use a ruler to carefully draw and measure the net. They measure and label the length and width of each face and calculate the area of each face on the net they have drawn. Once students have accurately drawn their nets and labeled the area of each side, a teacher will review their work. If it is an accurate net, the teacher will give the students a pair of scissors to cut it out. Make sure students do their calculations inside the net so that it is not lost when they cut it out. Once cut out, students can fold and tape their prism. Students found this activity to be more challenging than they expected. Several had to start over after realizing that the prism they started wouldn't fit on the page or their net wouldn't fold into a proper prism. You could extend this activity by having students tape their nets inside out (with the calculations on the inside) and then challenging them to order the prisms from least surface area to greatest surface area. Why I Like This Task
Double the Surface Area
Nova Scotia Mathematics Curriculum Outcomes Grade 8 M02 - Students will be expected to draw and construct nets for 3-D objects. Grade 8 M03 - Students will be expected to determine the surface area of right rectangular prisms, right triangular prisms, and right cylinders to solve problems. Grade 9 G01 - Students will be expected to determine the surface area of composite 3-D objects to solve problems Math at Work 11 M01 - Students will be expected to solve problems that involve SI and imperial units in surface area measurements and verify the solutions. EL
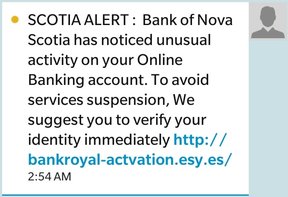
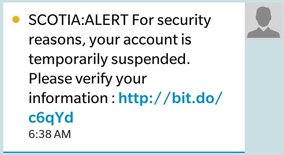
Text, Email and Phone PhishingIf I was playing some sort of financial scam bingo, I would surely be a winner. In the past three days, I've received phishing scam attempts through three different communication channels: text message, email and phone call. Two days ago I got a text message from the "Bank of Nova Scotia" alerting me to the fact that they had noticed unusual activity on my account. They suggested that I should go to a website to "verify my identity". In other words, they wanted me to give them my personal information (I don't have an account at Scotiabank). I recently learned that these types of text message scams are called "smishing" (short for "SMS phishing"). Yesterday I received an email from "RBC Royal Bank" letting me know that, "You have been locked out of your account!" Again, to unlock my account, I would have to visit a website and enter some personal information (I don't have an account at this bank either). Usually, these emails are blocked by my email providers spam blocker, but for some reason, this one sneaked through. This morning at 6:30 am, as I was getting my toddler dressed and ready for breakfast, I go a phone call. The caller, from an international phone number, greeted me by name and said his name was "Francis" and that he worked for the Visa Security Department. He wanted to alert me that someone had purchased a Western Union money transfer with my credit card and asked me to confirm the purchase. I told "Francis" that I would call Visa directly and hung up the phone. This early morning phone call credit card phishing scam has been around for a while, but this is the first time I got a call like this. Financial Literacy EducationThis recent surge in phishing scam attempts has highlighted the importance to me of teaching financial literacy to our students. High school students are at an age where they will soon be experiencing financial independence and need to make important decisions about budgeting, making purchases, investing and assuming debt such as student loans and credit cards. They will also have to learn how to protect themselves from fraud. The Nova Scotia high school mathematics curriculum contains a number of financial mathematics outcomes. These outcomes vary depending upon which mathematics courses a student takes. These outcomes deal with personal budgets, understanding pay and income, borrowing money, investing money and making purchases. Avoiding fraud and scams is not explicitly covered in any of these outcomes but could easily be included when teaching these topics. For example, when learning about banking services and credit cards, students could be taught how to recognize scams and what to do if they realize that they've been the victim of identity theft. They could also be taught how to keep their financial information secure and how they should and should not communicate with their bank and other financial institutions. The Canadian Anti-Fraud Centre maintains a list of fraud types and how to identify and report fraud. It is a very worthwhile website to check out: http://www.antifraudcentre-centreantifraude.ca/ Nova Scotia High School Mathematics Curriculum Outcomes relating to Finance Mathematics 10 - FM01, FM02, FM03, FM04 Math at Work 10 - N01, N02 Math Essentials 10 - Earning and Purchasing, Banking Math at Work 11 - N02, N03, N04, N05, A01 Math Essentials 11 - Housing, Banking Mathematics 12 - FM01, FM02, FM03 Math at Work 12 - N02, N03 EL
Sherman K. Stein, in the preface of his textbook Mathematics, The Man Made Universe, says "Mathematics is completely the work of man. Each theorem, each proof, is the product of the human mind. In mathematics all the cards can be put on the table. In this sense, mathematics is concrete, whereas the world is abstract." The order of operations is a mathematical convention that has been developed and refined over centuries by many mathematicians. Just about every student, at some point in their mathematical education, will run across the mnemonic BEDMAS (or PEDMAS if you live in the US). The usefulness of this mnemonic can be debated (Tina Cardone, the author of Nix the Tricks, wrote an article regarding this for the NCTM). I recently chatted with a teacher who was looking for resources to help his grade 7 students practice using the order of operations with decimal numbers. I created a "row game" for his students to practice this skill. A "row game" is an activity for students to work with a partner to evaluate a series of expressions. The expressions are written in two columns. One student evaluates the expressions in the left column and the other student evaluates the expressions in the right column. The expressions in each row evaluate to the same value. If the students don't get the same answer, they can work together to determine where the error was made. There are two reasons that I like row games. The first is that students get instant feedback. They don't need to wait for a teacher to correct and return a sheet to know if they are being successful. The second reason is that it gets students to work together to find their mistakes. The teacher can then focus on providing assistance to students who are having real conceptual difficulties, not just making small computational errors. Kate Nowak has created a shared Google drive folder where a large collection of row games are stored. A link to my row game for order of operations with decimals is below.
Confusion regarding the order of operations has lead to many debates and arguments on Facebook about the correct way to evaluate expressions. You might see expressions such as "6 ÷ 2(1 + 2)" or "48 ÷ 2(9 + 3)" discussed. These might be used to start a lively debate in math class. I really like Vi Hart's take on these types of problems. Take a moment to watch the video below. Vi's contention is that expressions like these are ambiguous and it is incumbent upon the author of the expression to add brackets or other grouping symbols to make their mathematical expression clear. The placement of implicit multiplication (sometimes called multiplication by juxtaposition or simply putting symbols side by side) in the order of operations has not been settled by mathematicians such that is is part of the convention for the order of operations. Despite this, calculators and computers have to make a decision on how to interpret this. You will find calculators that give different answers for these types of expressions. The Math Forum writes, "I suppose I agree with you that it would be easier and perhaps more consistent to give multiplication precedence over division everywhere; but of course there is no authority to decree this, so the more prudent approach is probably just to recognize that there really isn't any universal rule. " One method of avoiding this confusion is to write expressions is using Reverse Polish (RPN) notation. I'm old enough to have owned an HP calculator that used this notation. In RPN, the operator always follows all of its operands. For example, instead of writing "(1+2)÷(3+4)", you would write "1 2 + 3 4 + ÷". RPN often requires fewer key strokes to enter on a calculator because parentheses are not required. It is however more difficult to learn. Nova Scotia Mathematics Curriculum Outcomes Grade 9 N04 - Students will be expected to explain and apply the order of operations, including exponents, with and without technology. Grade 7 N02 - Students will be expected to demonstrate an understanding of the addition, subtraction, multiplication and division of decimals to solve problems (for more than one-digit divisors or more than two-digit multipliers, the use of technology is expected). EL
I recently read Knowing and Teaching Elementary Mathematics by Liping Ma. I really enjoyed this book and I wanted share my thoughts on some of its key messages. But first, a brief description of the book. The book compares the responses to a series of interview questions given to both US and Chinese elementary teachers. These quesions are part of the Teacher Education and Learning to Teach (TELT) Study. The four questions from the book deal with subtraction with regrouping, multidigit multiplication, division with fractions and the relationship between area and perimeter. Liping Ma analyses teachers' responses to discern how their understanding of mathematics influence how they instruct and respond to their students. Richard Askey wrote ane extensive review of Liping Ma's book for the American Educator, a journal of the American Federation of Teachers. The key message that I took from this book is the importance for teachers to develop a profound understanding of fundamental mathematics. Liping Ma describes this as having, "an understanding of the terrain of fundamental mathematics that is deep, broad, and thorough." (p. 120) It's through this conceptual understanding of elementary mathematics that teachers are able to think flexibly about mathematics, appreciate and understand a variety of methods for solving problems and respond to their students' novel ideas and questions. As Tracy Johnston Zager noted in her TMC16 keynote address, K-2 mathematics is not "the basics" rather it is, "student's introduction to what it means to do mathematics, what is math as a discipline" as well teaching kids "what it means to have a mathematical discussion, a mathematical idea, a mathematical question". Liping Ma says that "elementary mathematics is not a simple collection of disconnected number facts and calculational algorithms. Rather, it is an intellectually demanding, challenging, and exciting field - a foundation on which much can be built." (p. 116) Indeed, no matter what level of mathematics you teach, you should know it deeply and how it connects to related areas of mathematics. Liping Ma states, "Being able to calculate in multiple ways means that one has transcended the formality of an algorithm and reached the essence of the numerical operations - the underlying mathematical ideas and principles. The reason that one problem can be solved in multiple ways is that mathematics does not consist of isolated rules, but connected ideas. Being able to and tending to solve a problem in more than one way, therefore, reveals the ability and the predilection to make connections between and among mathematical areas and topics." (p. 112) One question that remains for me after reading this book is how teachers can best gain this profound understanding of mathematics. Liping Ma writes that, in China, teachers spend a significant amount of time studying teaching materials intensively. They closely exam both their curriculum guides and their textbooks. They study how the textbook has interpreted and presented the concepts in the curriculum and why the textbook's authors might have chosen this. Teachers review the examples and exercises in their textbook for each unit and reflect on the purpose of each exercise in relation to the curriculum outcomes. Teachers often spend significant time interacting with their teaching colleagues, "to share their ideas and reflections on teaching." (p. 136). The author notes that, "Time is an issue here. If teachers have to find out what to teach by themselves in their very limited time outside the classroom and decide how to teach it, then where is the time for them to study carefully what they are to teach? U.S. teachers have less working time outside the classroom than Chinese teachers, but they need to do much more in this limited time. What U.S. teachers are expected to accomplish, then is impossible. It is clear that they do not have enough time and appropriate support to think through thoroughly what they are to teach. And without a clear idea of what to teach, how can one determine how to teach it thoughtfully?" (p. 149). This is a current area of discussion in Nova Scotia, with working conditions being a significant issue in teachers' contract negotiations with the provincial government. The chapter in this book about division by fractions was especially timely. In the book, teachers were asked to how they determine the following quotient: 1 and 3/4 divided by 1/2. I recently had a conversation about the strategy of dividing fractions with a common denominator with a pair of junior high teachers (see Christopher Danielson's blog Overthinking my Teaching for a nice summary of this strategy). We discussed how the examples in the textbook were presented, what the curriculum guide had to say about this strategy, and how it could be used to enhance students' understanding of division. The discussion led me to investigate division of fractions more deeply (there is some great material on Ontario's EduGains website). This type of conversation is what Liping Ma suggests helps to promote a deeper understanding of mathematical content, and in my experience, has been a benefit of teachers' professional learning communities. If you are interesting in other teachers relfections on this book, below are two excellent blog posts to read: EL
|
Categories
All
|
||||||||||






 RSS Feed
RSS Feed